Kvadrantti on määritelty alueeksi avaruudessa, joka on jaettu neljään yhtä suureen osaan kahdella akselilla, nimittäin X-akselilla ja Y-akselilla suorakulmaisessa tasossa. Nämä kaksi akselia leikkaavat toisensa 90 asteen kulmassa ja näin muodostettuja neljää aluetta kutsutaan neljäksi kvadrantiksi, nimittäin I kvadrantiksi, II kvadrantiksi, III neljännekseksi ja IV neljännekseksi.
tehdä skriptistä suoritettavaa
Tässä artikkelissa tutkimme keskeisiä kvadrantin käsitteitä, mukaan lukien mitä kvadrantti on, sen pinta-alaa, kvadranttikaaviota, karteesista tasoa, kvadrantin sisäisiä merkkisopimuksia, abskissaa ja koordinaattia sekä pisteiden piirtämistä kvadrantissa.
Sisällysluettelo
- Mitä ovat graafin neljännekset?
- Allekirjoita sopimus kvadranteissa
- Pisteiden piirtäminen kvadranteissa
- Trigonometriset arvot eri kvadranteissa
Mitä ovat graafin neljännekset?
Kvadrantti on määrätty alue a Karteesinen taso , joka on luotu X- ja Y-akselien leikkauspisteestä. Tässä tasossa muodostuu neljä kvadranttia, joista jokaisella on ainutlaatuiset piirteensä. Ensimmäisellä kvadrantilla oikeassa yläkulmassa on positiiviset x- ja y-koordinaatit. Toisessa kvadrantissa vasemmassa yläkulmassa on negatiiviset x- ja positiiviset y-koordinaatit ja niin edelleen. Näiden kvadranttien ymmärtäminen on välttämätöntä kaavion pisteiden paikallistamiseksi ja tulkitsemiseksi, mikä tarjoaa systemaattisen tavan navigoida ja analysoida suorakulmaisia koordinaatteja.
4 kvadranttia koordinaattitasolla
X- ja Y-akselien muodostama karteesinen taso on jaettu neljään kvadranttiin, joilla jokaisella on omat ominaisuudet:
- Ensimmäinen kvadrantti: Oikeassa yläkulmassa sekä x- että y-koordinaatit ovat positiivisia. Tämä kvadrantti edustaa pisteitä tason oikeassa yläkulmassa.
- Toinen kvadrantti: Vasemmassa yläkulmassa oleva x-koordinaatti on negatiivinen ja y-koordinaatti on positiivinen. Tämä kvadrantti kattaa tason vasemmassa yläkulmassa olevat pisteet.
- Kolmas kvadrantti: Vasemmassa alakulmassa sekä x- että y-koordinaatit ovat negatiivisia. Tason vasemmassa alakulmassa olevat pisteet kuuluvat tähän neljännekseen.
- Neljäs kvadrantti: Löytyy oikeasta alakulmasta, x-koordinaatti on positiivinen ja y-koordinaatti on negatiivinen. Tämä kvadrantti sisältää pisteitä tason oikeassa alakulmassa.
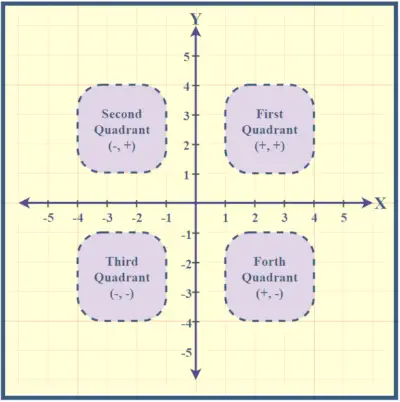
Kvadrantit on numeroitu vastapäivään oikeasta yläkulmasta alkaen. Pistettä, jossa X- ja Y-akselit leikkaavat, kutsutaan origoksi, jonka koordinaatit (0,0) osoittavat nolla-arvoja sekä x:lle että y:lle. Näiden kvadranttien ymmärtäminen auttaa paikantamaan pisteitä suorakulmaisella tasolla.
Mikä on Origin?
Kaavion aloituspiste, joka tunnetaan nimellä origo ja näytetään (0, 0), on kohta, jossa vaakasuuntainen x-akseli ja pystysuora y-akseli leikkaavat. Tämä tarkoittaa, että origossa sekä x:n että y:n arvot ovat nolla. Se toimii vertailupisteenä kaavion muiden pisteiden paikantamiseksi. Yllä lisätyssä kuvassa piste O näyttää origon.
Abskissa ja ordinaatta kvadranteissa
Neljässä kvadrantissa numerot esitetään pareina (a, b), joissa 'a' tarkoittaa x-koordinaattia ja 'b' on y-koordinaatti. Selvittääksesi missä piste on ilman piirtämistä, kiinnitä huomiota x-koordinaatin (abskissa) ja y-koordinaatin (ordinaatin) merkkeihin. Jos sinulla on esimerkiksi piste, kuten Q (3, -5), merkit (+ve, -ve) osoittavat, että se on neljännessä IV.
Abskissa näyttää vaakaetäisyyden Y-akselista. Positiivinen abskissa tarkoittaa oikealle, ja esimerkissämme abskissa = 3 tarkoittaa siirtymistä oikealle origosta x-akselia pitkin 3 yksikköä.
Ordinaatta osoittaa pystysuoran etäisyyden origosta. Negatiivinen ordinaatta tarkoittaa siirtymistä alas origosta y-akselia pitkin. Esimerkissä ordinate = -5 tarkoittaa, että laskee 5 yksikköä.
Allekirjoita sopimus kvadranteissa
Kvadranttien merkkisopimukset voidaan helposti ymmärtää alla olevan kuvan avulla,

Kun siirrymme XY-tasossa vasemmalta oikealle x-akselia pitkin, x-koordinaatti kasvaa. Vastaavasti y-akselia pitkin siirtyminen alhaalta ylös johtaa y-koordinaatin kasvuun. XY-taso on jaettu neljään kvadranttiin, joista jokaisella on erityiset merkkisopimukset x- ja y-koordinaateille:
| Kvadrantti | x-koordinaatti | y-koordinaatti |
|---|---|---|
| 1. kvadrantti | Positiivinen (+) | Positiivinen (+) |
| 2. kvadrantti | Negatiivinen (-) | Positiivinen (+) |
| 3. kvadrantti | Negatiivinen (-) | Negatiivinen (-) |
| 4. kvadrantti | Positiivinen (+) | Negatiivinen (-) |
Siksi 1. kvadrantin pisteillä on positiiviset arvot sekä x:lle että y:lle, 2. neljänneksellä on negatiivinen x ja positiivinen y, 3. neljänneksellä on sekä negatiiviset x- että y-arvot ja 4. neljänneksellä on positiivinen x ja y:n arvo. negatiivinen y.
Pisteiden piirtäminen kvadranteissa
Karteesisessa tasossa pisteet tunnistetaan x-akselilla ja y-akselilla. Nämä pisteet merkitään (a, b), missä 'a' on x-koordinaatti (abskissa) ja 'b' on y-koordinaatti (ordinaatta). Asettaaksemme pisteen kvadrantissa otamme huomioon näiden koordinaattien merkit. Arvot x ja y edustavat, kuinka kaukana piste on vastaavasti x-akselista ja y-akselista.
Piirrä esimerkiksi piste (2, -5) suorakulmaiselle tasolle. Koordinaattien etumerkkiä analysoimalla paljastuu, että piste on neljännessä neljänneksessä. Se on 2 yksikön päässä x-akselista (oikealla) ja 5 yksikön päässä y-akselista (alas), käyttämällä origoa vertailupisteenä.
Trigonometriset arvot eri kvadranteissa
Eri arvot trigonometriset funktiot eri kvadranteissa voidaan oppia tutkimalla alla olevaa taulukkoa,
| Kvadrantti varhaiset mukerit | Ilman | Cos | Niin | Kosekantti | Sekantti | Kotangentti |
|---|---|---|---|---|---|---|
| 1. kvadrantti | + | + | + | + | + | + |
| 2. kvadrantti | + | – | + | + | – | – |
| 3. kvadrantti | – | – | – | – | – | + |
| 4. kvadrantti | – | – | – | – | + | – |
Ensimmäisessä kvadrantissa kaikki trigonometriset suhteet ovat positiivisia. Toisessa kvadrantissa sini ja kosekantti ovat positiivisia (+), kun taas kosini ja sekantti ovat negatiivisia (-). Kolmannessa kvadrantissa Tangentti ja Cotangent ovat positiivisia (+), kun taas kosini ja sekantti ovat negatiivisia (-). Neljännessä kvadrantissa sini ja kosekantti ovat negatiivisia (-), kun taas kosini ja sekantti ovat positiivisia (+).
java string.format
Lue lisää,
- Koordinaattigeometria
- Yhdensuuntaiset viivat
- Etäisyyden kaava
Ratkaistut esimerkit Quadrantissa
Esimerkki 1: Piirrä piste A (3, -4) ja tunnista sen kvadrantti.
Ratkaisu:
Piste A sijaitsee koordinaateissa (3, -4). Koska x-koordinaatti on positiivinen (3) ja y-koordinaatti on negatiivinen (-4), piste A sijaitsee neljänneksessä IV.
Esimerkki 2: Piirrä piste P (-5, 2) ja määritä sen kvadrantti
Ratkaisu:
Pisteen P koordinaatit ovat (-5, 2). Kvadrantin määrittämiseksi tutkimme x- ja y-koordinaattien etumerkkejä.
X-koordinaatti on -5, mikä osoittaa sijaintia origosta vasemmalla.
Y-koordinaatti on 2, mikä osoittaa sijaintia origon yläpuolella.
Siksi, koska x-koordinaatti on negatiivinen ja y-koordinaatti on positiivinen, piste P sijaitsee kvadrantissa II.
Piste P (-5, 2) sijaitsee suorakulmaisen tason kvadrantissa II.
Harjoittele kvadranttien ongelmia
Ongelma 1: Piirrä piste (1, -1) ja tunnista sen kvadrantti.
Ongelma 2: Etsi kolme pistettä x-akselilta ja määritä niiden kvadrantit.
Ongelma 3: Jos piste sijaitsee y-akselilla koordinaateilla (0, -3), missä neljänneksessä se on?
Ongelma 4: Etsi pisteet Q (2, 2), R (-2, -2) ja S (0, 0) ja tarkista kollineaarisuus.
Ongelma 5: Piirrä piste (-4, -3) ja selitä missä kvadrantissa se sijaitsee.
Kvadrantteja koskevat usein kysytyt kysymykset
1. Mikä on kvadrantti matematiikassa?
Matematiikassa kvadrantti on yksi neljästä osasta, jotka on luotu kahden kohtisuoran suoran tai akselin leikkauspisteessä. Nämä akselit on tyypillisesti merkitty x-akseliksi ja y-akseliksi suorakulmaisessa koordinaattijärjestelmässä.
2. Mitä kutsutaan kahden akselin leikkauspisteeksi?
Kahden akselin leikkauskohtaa suorakulmaisessa koordinaatistossa kutsutaan origoksi. Sitä edustaa piste, jossa x-akseli ja y-akseli kohtaavat, yleensä merkitty (0,0).
3. Mitä ovat 4 kvadranttia?
Neljä kvadranttia ovat leikkeitä, jotka muodostetaan jakamalla suorakulmainen koordinaattitaso neljään yhtä suureen osaan. Ne on merkitty ensimmäiseksi kvadrantiksi (Q1), toiseksi kvadrantiksi (Q2), kolmanneksi neljännekseksi (Q3) ja neljänneksi neljännekseksi (Q4).
4. Mikä kvadrantti on positiivinen?
Positiivinen kvadrantti suorakulmaisessa koordinaatistossa on ensimmäinen neljännes (Q1). Tässä kvadrantissa sekä x- että y-koordinaatit ovat positiivisia.
5. Mikä on kvadranttien käyttö kaavioissa?
Kaavioiden neljännekset tarjoavat systemaattisen tavan järjestää ja paikantaa pisteitä niiden koordinaattien perusteella. Ne auttavat visualisoimaan muuttujien välisiä suhteita ja analysoimaan tietojoukkojen kuvioita, mikä helpottaa graafisten esitusten tulkintaa.
6. Millä neljänneksellä on molemmat positiiviset koordinaatit?
Ensimmäinen kvadrantti (Q1) on kvadrantti, jossa sekä pisteiden x- että y-koordinaatit ovat positiivisia. Se on ainoa kvadrantti, jolla on molemmat positiiviset arvot.
7. Mitkä ovat ympyrän 4 kvadranttia?
Kvadranttien käsite ei sovellu suoraan ympyröihin. Sen sijaan ympyrät jaetaan kulmiin, jotka mitataan asteina. Jos kuitenkin viitataan pyöreisiin sektoreihin, voidaan käyttää termejä kuten ensimmäinen sektori, toinen sektori, kolmas sektori ja neljäs sektori, jotka vastaavat eri kulma-alueita.
