logo

TechCodeview

Kvantiili Quantile-kuvat

Kvantiili-kvantiili (q-q plot) -kaavio on graafinen menetelmä sen määrittämiseksi, noudattaako tietojoukko tiettyä todennäköisyysjakaumaa vai onko kaksi datanäytettä peräisin samasta väestö tai ei. Q-Q-kuvaajat ovat erityisen hyödyllisiä arvioitaessa, onko tietojoukko normaalisti jakautunut tai jos se seuraa jotain muuta tunnettua jakaumaa. Niitä käytetään yleisesti tilastoissa, data-analyysissä ja laadunvalvonnassa oletusten tarkistamiseen ja odotettujen jakaumien poikkeamien tunnistamiseen.

Kvantiilit ja prosenttipisteet

Kvantiilit ovat tietojoukon pisteitä, jotka jakavat tiedot intervalleiksi, jotka sisältävät yhtä suuret todennäköisyydet tai osuudet kokonaisjakaumasta. Niitä käytetään usein kuvaamaan tietojoukon leviämistä tai jakautumista. Yleisimmät kvantiilit ovat:



  1. Mediaani (50. prosenttipiste) : Mediaani on tietojoukon keskiarvo, kun se on järjestetty pienimmästä suurimpaan. Se jakaa tietojoukon kahteen yhtä suureen puolikkaaseen.
  2. Quartiles (25., 50. ja 75. prosenttipisteet) : Kvartiilit jakavat tietojoukon neljään yhtä suureen osaan. Ensimmäinen kvartiili (Q1) on arvo, jonka alapuolelle jää 25 % tiedoista, toinen kvartiili (Q2) on mediaani ja kolmas kvartiili (Q3) on arvo, jonka alapuolelle 75 % tiedoista jää.
  3. Persentiilit : Persentiilit ovat samanlaisia ​​kuin kvartiileja, mutta jakavat tietojoukon 100 yhtä suureen osaan. Esimerkiksi 90. prosenttipiste on arvo, jonka alapuolelle 90 % tiedoista jää.

Huomautus:

  • Q-q-kuvaaja on ensimmäisen tietojoukon kvantiilien kuvaaja toisen tietojoukon kvantiileja vastaan.
  • Viitetarkoituksia varten piirretään myös 45 %:n viiva; varten jos näytteet ovat samasta populaatiosta, pisteet ovat tällä viivalla.


Normaalijakauma:

Normaalijakauma (alias Gaussin jakauman Bell-käyrä) on jatkuva todennäköisyysjakauma, joka edustaa satunnaisesti generoiduista reaaliarvoista saatua jakaumaa.

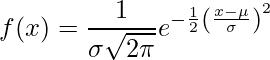
. {displaystyle f(x)={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x -mu }{sigma }} ight)^{2}}}



f(x) = Todennäköisyys , Jakauma , Funktio mu = keskiarvo sigma = standardi , poikkeama


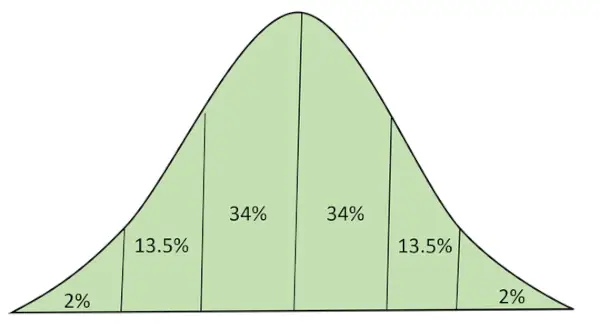
Normaali jakautuminen käyrän alla olevalla alueella




Kuinka piirtää Q-Q juoni?

Voit piirtää kvantiili-kvantiili (Q-Q) -kaavion seuraavasti:

  1. Kerää tiedot : Kerää tietojoukko, jolle haluat luoda Q-Q-kaavion. Varmista, että tiedot ovat numeerisia ja edustavat satunnaista otosta kiinnostavasta populaatiosta.
  2. Lajittele tiedot : Järjestä tiedot joko nousevaan tai laskevaan järjestykseen. Tämä vaihe on välttämätön kvantiilien tarkkaan laskemiseen.
  3. Valitse teoreettinen jakauma : Määritä teoreettinen jakauma, johon haluat verrata tietojoukkoasi. Yleisiä valintoja ovat normaalijakauma, eksponentiaalinen jakauma tai mikä tahansa muu jakauma, joka sopii hyvin tietoihisi.
  4. Laske teoreettiset kvantiilit : Laske valitun teoreettisen jakauman kvantiilit. Jos esimerkiksi vertailet normaalijakaumaan, käytät normaalijakauman käänteistä kumulatiivista jakaumafunktiota (CDF) odotettujen kvantiilien löytämiseen.
  5. Piirustus :
    • Piirrä lajitellut tietojoukon arvot x-akselille.
    • Piirrä vastaavat teoreettiset kvantiilit y-akselille.
    • Jokainen datapiste (x, y) edustaa havaittujen ja odotettujen arvojen paria.
    • Yhdistä tietopisteet tarkastellaksesi visuaalisesti tietojoukon ja teoreettisen jakauman välistä suhdetta.


Q-Q-kaavion tulkinta

  • Jos käyrän pisteet putoavat suunnilleen suoraa linjaa pitkin, se viittaa siihen, että tietojoukosi noudattaa oletettua jakaumaa.
  • Poikkeamat suorasta viivasta osoittavat poikkeamia oletetusta jakaumasta, mikä vaatii lisätutkimuksia.

Jakauman samankaltaisuuden tutkiminen Q-Q-kaavioiden avulla


Jakauman samankaltaisuuden tutkiminen Q-Q-kaavioiden avulla on tilastojen perustehtävä. Kahden tietojoukon vertaaminen sen määrittämiseksi, ovatko ne peräisin samasta jakaumasta, on elintärkeää eri analyyttisiin tarkoituksiin. Kun oletus yhteisestä jakaumasta pätee, tietojoukkojen yhdistäminen voi parantaa parametrien arvioinnin tarkkuutta, kuten sijainnin ja mittakaavan osalta. Q-Q-kuvaajat, lyhenne sanoista kvantiili-kvantiilikuvaajat, tarjoavat visuaalisen menetelmän jakauman samankaltaisuuden arvioimiseen. Näissä käyrissä yhden tietojoukon kvantiilit piirretään toisen kvantiileja vastaan. Jos pisteet ovat tiukasti linjassa diagonaaliviivaa pitkin, se viittaa jakaumien samanlaisuuteen. Poikkeamat tästä diagonaaliviivasta osoittavat eroja jakautumisominaisuuksissa.

Vaikka testit, kuten chi-neliö ja Kolmogorov-Smirnov testeillä voidaan arvioida yleisiä jakautumaeroja, Q-Q-kuvaajat tarjoavat vivahteikkaat näkökulmat vertaamalla suoraan kvantiileja. Tämä antaa analyytikot havaita erityisiä eroja, kuten sijainnin tai mittakaavan muutoksia, jotka eivät välttämättä ole ilmeisiä pelkästään muodollisista tilastollisista testeistä.

Q-Q-kaavion Python-toteutus

Python 3

import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> 
>
>

Lähtö:



Q-Q juoni


Tässä, koska datapisteet seuraavat suunnilleen suoraa viivaa Q-Q-kaaviossa, se viittaa siihen, että tietojoukko on yhdenmukainen oletetun teoreettisen jakauman kanssa, jonka tässä tapauksessa oletettiin olevan normaalijakauma.

Q-Q juonen edut

  1. Joustava vertailu : Q-Q-kuvaajat voivat verrata erikokoisia tietojoukkoja ilman vaativat samankokoisia näytteitä.
  2. Dimensioton analyysi : Ne ovat ulottumattomia, joten ne soveltuvat tietojoukkojen vertailuun eri yksiköitä tai asteikkoja.
  3. Visuaalinen tulkinta : Tarjoaa selkeän visuaalisen esityksen tietojen jakautumisesta verrattuna teoreettiseen jakaumaan.
  4. Herkkä poikkeamille : Havaitsee helposti poikkeamat oletetuista jakaumista, mikä auttaa tunnistamaan tietoerot.
  5. Diagnostiikkatyökalu : Auttaa arvioimaan jakautumisoletuksia, tunnistamaan poikkeavia arvoja ja ymmärtämään tietomalleja.

Kvantiili-kvantiilikuvan sovellukset

Kvantiili-kvantiili-kaaviota käytetään seuraavaan tarkoitukseen:

  1. Jakeluoletusten arviointi : Q-Q-kaavioita käytetään usein visuaalisesti tarkastamaan, noudattaako tietojoukko tiettyä todennäköisyysjakaumaa, kuten normaalijakaumaa. Vertaamalla havaitun datan kvantiileja oletetun jakauman kvantiileihin voidaan havaita poikkeamia oletetusta jakaumasta. Tämä on ratkaisevan tärkeää monissa tilastollisissa analyyseissä, joissa jakautumisoletusten paikkansapitävyys vaikuttaa tilastollisten päätelmien tarkkuuteen.
  2. Poikkeamien havaitseminen : Outliers ovat tietopisteitä, jotka poikkeavat merkittävästi muusta tietojoukosta. Q-Q-kaaviot voivat auttaa tunnistamaan poikkeamat paljastamalla datapisteitä, jotka ovat kaukana odotetusta jakauman mallista. Poikkeamat voivat näkyä pisteinä, jotka poikkeavat kaaviossa odotetusta suorasta.
  3. Jakelujen vertailu : Q-Q-kaavioita voidaan käyttää kahden tietojoukon vertaamiseen sen selvittämiseksi, ovatko ne peräisin samasta jakaumasta. Tämä saavutetaan piirtämällä yhden tietojoukon kvantiilit toisen tietojoukon kvantiileja vastaan. Jos pisteet osuvat suunnilleen suoraa linjaa pitkin, se viittaa siihen, että kaksi tietojoukkoa on piirretty samasta jakaumasta.
  4. Normaaliuden arviointi : Q-Q-kuvaajat ovat erityisen hyödyllisiä arvioitaessa tietojoukon normaaliutta. Jos datapisteet kuvaajassa seuraavat tarkasti suoraa viivaa, se osoittaa, että tietojoukko on likimäärin normaalijakautumassa. Poikkeamat viivasta viittaavat poikkeamiin normaalista, mikä saattaa vaatia lisätutkimuksia tai ei-parametrisia tilastotekniikoita.
  5. Mallin validointi : Aloilla, kuten ekonometria ja koneoppiminen, Q-Q-kaavioita käytetään ennustavien mallien validointiin. Vertaamalla havaittujen vasteiden kvantiileja mallin ennustamiin kvantiileihin voidaan arvioida, kuinka hyvin malli sopii dataan. Poikkeamat odotetusta mallista voivat osoittaa alueita, joilla mallia on parannettava.
  6. Laadunvalvonta : Q-Q-käyriä käytetään laadunvalvontaprosesseissa mitattujen tai havaittujen arvojen jakautumisen seuraamiseen ajan kuluessa tai eri erissä. Poikkeamat kaavion odotetuista malleista voivat merkitä muutoksia taustalla olevissa prosesseissa, mikä saa aikaan lisätutkimuksia.

Q-Q-kaavioiden tyypit

Tilastoissa ja data-analyysissä käytetään yleisesti useita Q-Q-kaavioita, joista jokainen sopii eri skenaarioihin tai tarkoituksiin:

  1. Normaalijakauma : Symmetrinen jakauma, jossa Q-Q-kuvaaja näyttäisi pisteitä suunnilleen diagonaalista viivaa pitkin, jos tiedot noudattavat normaalijakaumaa.
  2. Oikealle vino jakelu : Jakauma, jossa Q-Q-kaavio näyttäisi kuvion, jossa havaitut kvantiilit poikkeavat suorasta viivasta kohti yläpäätä, mikä osoittaa pidempää häntää oikealla puolella.
  3. Vasemmalle vino jakelu : Jakauma, jossa Q-Q-käyrä osoittaisi kuvion, jossa havaitut kvantiilit poikkeavat suorasta viivasta kohti alapäätä, mikä osoittaa pidempää häntää vasemmalla puolella.
  4. Alihajautunut jakelu : Jakauma, jossa Q-Q-käyrä näyttäisi havaitut kvantiilit ryhmittyneinä tiukemmin diagonaaliviivan ympärille verrattuna teoreettisiin kvantiileihin, mikä viittaa pienempään varianssiin.
  5. Ylihajautunut jakelu : Jakauma, jossa Q-Q-käyrä näyttäisi hajautetuimpia tai diagonaaliviivasta poikkeavia kvantiileja, mikä osoittaa suurempaa varianssia tai hajontaa verrattuna teoreettiseen jakaumaan.

Python 3

import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>>1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> 
>
>

Lähtö:


Q-Q-kaavio eri jakaumille

pd.merge