A Jonon tietorakenne on tietojenkäsittelytieteen peruskäsite, jota käytetään tietojen tallentamiseen ja hallintaan tietyssä järjestyksessä. Se noudattaa periaatetta Ensimmäinen sisällä ensimmäinen ulkona (FIFO) , jossa ensimmäinen jonoon lisätty elementti on ensimmäinen, joka poistetaan. Jonoja käytetään yleisesti erilaisissa algoritmeissa ja sovelluksissa niiden yksinkertaisuuden ja tehokkuuden vuoksi tietovirran hallinnassa.

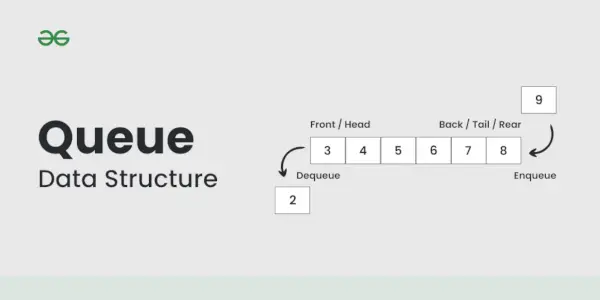
Jonon tietorakenne

Sisällysluettelo

• Jonon sovellukset
• Queuen toteutukset eri ohjelmointikielillä
• Mikä on jono tietorakenteissa?

  Jono on lineaarinen tietorakenne, joka seuraa First-in-First-Out (FIFO) periaate. Se toimii kuin viiva, jonka toiseen päähän lisätään elementtejä ( takaosa ) ja poistetaan toisesta päästä ( edessä ).

  Poista jonosta (poista) : Poistaa ja palauttaa elementin jonon etuosasta.

• Kurkistaa : Palauttaa jonon alussa olevan elementin poistamatta sitä.
• Tyhjä : Tarkistaa, onko jono tyhjä.
• Koko : Tarkistaa, onko jono täynnä.

• Jono C++ Standard Template Libraryssa (STL)
• Jonokäyttöliittymä Javassa
• Jono Pythonissa
• Jono C#:ssa
• Jono Javascriptissä

Toteuta pino käyttämällä yhtä jonoa

Toteuta jono pinojen avulla

Kuinka tehokkaasti toteuttaa k jonoa yhdessä taulukossa?

LRU-välimuistin toteutus

Havaitse sykli ohjaamattomassa graafissa käyttämällä BFS:ää

Leveys ensin -haku tai BFS kaaviolle

Hakemiston läpikulku Javassa BFS:n avulla

Binaaripuun pystysuuntainen läpikulku kartalla

Tulosta oikea näkymä binaaripuusta

Etsi binaaripuun vähimmäissyvyys

Tarkista, onko annettu graafi Bipartite vai ei

Taso maksimimäärällä solmuja

Selvitä, onko suunnatun graafin kahden kärjen välillä polku

Tulosta kaikki solmut kahden tietyn tason välillä binaaripuussa

Etsi annetun avaimen seuraava oikea solmu

Vähimmäisaskel Ritarin saavuttamiseksi

Saaret kaaviossa BFS:n avulla

Tasojärjestyksen läpikulku rivi riviltä | Sarja 3 (yhdellä jonolla)

Etsi ensimmäinen ei-toistuva merkki merkkivirrasta

Flood Fill Algorithm

Kaikkien appelsiinien mätänemiseen tarvittava vähimmäisaika

Lyhin polku binaarisessa sokkelossa

Mielenkiintoinen menetelmä binäärilukujen luomiseksi 1:stä n:ään

Suurin kustannuspolku lähdesolmusta määränpäähän

Lyhin etäisyys kahden solun välillä matriisissa tai ruudukossa

Käärme- ja tikapuuongelma

Etsi lyhin turvallinen reitti polulla, jossa on maamiinoja

Laske kaikki mahdolliset kävelyt lähteestä määränpäähän tarkalleen K reunalla

Kahden solmun välisen yksinkertaisen polun vähimmäiskustannukset suunnatussa ja painotetussa kaaviossa

Minimikustannuspolku suunnatussa kaaviossa tietyn välisolmujoukon kautta

Löydä ensimmäinen pyöreä esittely, joka vierailee kaikissa bensiinipumpuissa

Pikalinkit:

• 'Videot' jonossa
• Suositus:
  • Opi tietorakenne ja algoritmit | DSA opetusohjelma
  • Jono Go-kielellä
  • Jono Scalassa