Kaltevuuskaavaa käytetään määrittämään viivan jyrkkyys tai kaltevuus. Suoralla olevien pisteiden x- ja y-koordinaatteja käytetään suoran kaltevuuden laskemiseen. Y-koordinaatin muutosta, joka koskee x-koordinaattien muutosta, kutsutaan suoran kaltevuudeksi ja sitä kuvataan yleensä kirjaimella m.

Sisällysluettelo

• Mikä on Slope Formula?
• Kaltevuuskaava
• Kaltevuuskaavan johtaminen
• Viivan kaltevuus (suoraviiva) -kaava
• Kaltevuusyhtälö
• Esimerkki Slope Formulasta

Mikä on Slope Formula?

Viivan kaltevuuden laskemiseen tarvitaan kaltevuuskaava. Suoran kaltevuuden laskemiseksi tarvitaan viivan pisteiden x- ja y-koordinaatit. Y-koordinaattien muutoksen ja x-koordinaattien muutoksen suhdetta kutsutaan suoran kaltevuudeksi.

Kulmakerroin (m) = muutos y:ssä/muutos x:ssä = Δy/Δx

Kaltevuuskaava

Matematiikassa viivan jyrkkyyttä käytetään määrittämään, kuinka paljon viiva on kallistunut, eli viivan jyrkkyyttä. Viivan kaltevuuden määrittämiseksi tarvitsemme viivalla olevien pisteiden x- ja y-koordinaatit. Kaltevuuskaava on y-koordinaatin nettomuutos jaettuna x-koordinaatin nettomuutoksella. Δy on muutos y-koordinaateissa ja Δx on muutos x-koordinaateissa. Siten y-koordinaattien muutoksen suhde x-koordinaattien muutokseen saadaan seuraavasti:

Kulmakerroin (m) = muutos y:ssä/muutos x:ssä = Δy/Δx

m = (ja ₂ - ja ₁ )/(x ₂ – x ₁ )

missä

• x₁ja x₂ovat X-akselin koordinaatit
• ja₁ja y₂ovat Y-akselin koordinaatit

Kaltevuuskaavan johtaminen

Viivan x- ja y-koordinaatteja käytetään suoran kaltevuuden laskemiseen. Nettomuutos y-koordinaatissa on Δy, kun taas nettomuutos x-koordinaatissa on Δx. Joten y-koordinaatin muutos suhteessa x-koordinaatin muutokseen voidaan kirjoittaa seuraavasti:

m = Δy/Δx

missä,

• m on rinne
• Δy on muutos y-koordinaateissa
• Δx on x-koordinaattien muutos

Tiedämme, että tan θ on myös suoran kaltevuus, jossa θ on kulma, jonka suora muodostaa x-akselin positiivisen suunnan kanssa.

Ja, tan θ = korkeus/pohja

Koska kahden tietyn pisteen välinen korkeus/pohja = (y₂- ja₁)/(x₂– x₁)

Siten kaltevuusyhtälö on, m = tan θ = Δy/Δx

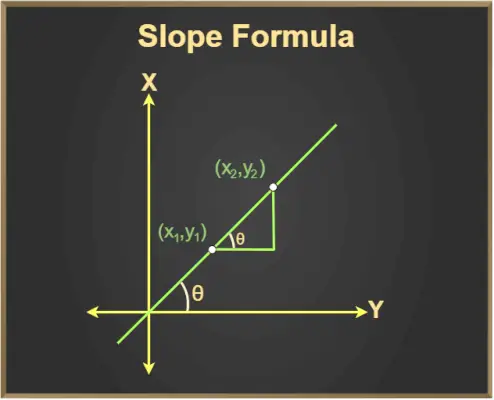
Kaaviosta huomaamme:

matriisiohjelma c-kielellä

Δy = (y₂- ja₁)

Δx = (x₂– x₁)

Sitten kaltevuuskaava annetaan seuraavasti:

Kaltevuus = m = (y ₂ - ja ₁ )/(x ₂ – x ₁ )

Viivan kaltevuus (suoraviiva) -kaava

• Tiedämme sen tan θ on myös viivan kaltevuus, joten viivan kaltevuus voidaan esittää myös muodossa,

Kaltevuus (m) = tan θ = Δy/Δx

Missä i on kulma, jonka viiva w.r.t muodostaa positiiviseen X-akseliin,

• Δy = muutos y-koordinaateissa,
• Δx = muutos x-koordinaateissa.

• Voimme myös määritellä viivan kaltevuuden nousun suhteeksi juoksuun.

Kaltevuus (m) = nousu/juoksu

• Olkoon ax + by + c = 0 suoran yleinen yhtälö. Nyt viivan kaltevuuden kaava on annettu kaavalla,

Kaltevuus (m) = – x:n kerroin / y:n kerroin = -a/b

• Suoran kaltevuusleikkausmuoto viivayhtälöä käyttäen annetaan seuraavasti:

y = mx + c

Missä m on suoran kaltevuus ja c on suoran y-leikkaus.

Kaltevuusyhtälö

Kaltevuuskaavaa käytetään määrittämään viivan kaltevuus. Kaltevuuden löytämiseen käytetty yhtälö kirjoitetaan seuraavasti:

m = tanθ = Δy/Δx = (y ₂ - ja ₁ )/(x ₂ – x ₁ )

lisää taulukkoon java

missä,

• m on viivan kaltevuus
• Δy on ero y-koordinaateissa
• Δx on ero x-koordinaateissa
• i on positiivisen x-akselin linjan muodostama kulma

Suoran yhtälö kaltevuuden m kanssa saadaan kaavalla,

y = mx + c

missä,

• m on viivan kaltevuus
• b on suoran y-leikkauspiste

Lue lisää,

Androidin kehittäjätilan sammuttaminen

• Yhdensuuntaiset viivat
• Slope Intercept -lomake

Esimerkki Slope Formulasta

Esimerkki 1: Etsi sellaisen suoran kaltevuus, jonka koordinaatit ovat (3, 7) ja (5, 8).

Ratkaisu:

Annettu, (x₁, ja₁) = (3,7) ja (x₂, ja₂) = (5,8)

Kaltevuuskaava (m) = (y ₂ - ja ₁ )/(x ₂ – x ₁ )

⇒ m = (8 – 7)/(5 – 3) = 1/2

Näin ollen annetun suoran kaltevuus on 1/2.

Esimerkki 2: Määritä sellaisen suoran kaltevuus, jonka koordinaatit ovat (7, -5) ja (2, -3).

Ratkaisu:

Annettu, (x₁, ja₁) = (7, -5) ja (x₂, ja₂) = (23)

Kaltevuuskaava (m) = (y ₂ - ja ₁ )/(x ₂ – x ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Näin ollen annetun suoran kaltevuus on -2/5

Esimerkki 3: Etsi a:n arvo, jos pisteiden (-4, a) ja (2, 5) kautta kulkevan suoran kaltevuus on 3.

Ratkaisu:

Annettu, (x₁, ja₁) = (4,a) ja (x₂, ja₂) = (2, 5) ja kaltevuus (m) = 3

Tiedämme, että kaltevuus (m) = (y ₂ - ja ₁ )/(x ₂ – x ₁ )

⇒ 3 = (5 – a)/(2 – 4)

⇒ 3 = (5 – a)/(-2)

⇒ -6 = 5 – a ⇒ a = 5 + 6 = 11

Näin ollen a = 11

Esimerkki 4: Jos suora muodostaa 60° kulman positiivisen Y-akselin kanssa, niin mikä on suoran kaltevuuden arvo?

xvideoservicethief ubuntu 14.04 lataus

Ratkaisu:

Annetut tiedot, positiivisen y-akselin linjan muodostama kulma = 60°

Tiedämme, että jos viiva muodostaa 60° kulman positiivisesta y-akselista, niin se muodostaa kulman (90° – 60° = 30°) x-akselin kanssa.

Siksi viivan kaltevuuden arvo (m) = tan 30° = 1/√3

Siten suoran kaltevuuden arvo = 1/√3.

Esimerkki 5: Sheela tarkisti kaaviota ja huomasi, että korotus oli 12 yksikköä ja juoksu 4 yksikköä. Laske nyt viivan kaltevuus.

Ratkaisu:

Annetut tiedot, nousu = 12 yksikköä ja juoksu = 4 yksikköä

Tiedämme, että kaltevuus (m) = nousu/juoksu

⇒ m = 12/4 = 3

Siksi annetun suoran kaltevuus on 3

Esimerkki 6: Etsi suoran kaltevuus 3x – 7y + 8 = 0.

Ratkaisu:

Annetut tiedot, suoran yhtälö = 3x – 7y + 8 = 0

Vertaa nyt annettua suoran yleisyhtälöön eli ax + by + c = 0

Siksi a = 3, b = -7 ja c = 8

Tiedämme, että kulmakerroin (m) = – x:n kerroin/y:n kerroin = -a/b

⇒ m = -3/(-7) = 3/7

Näin ollen annetun viivan kaltevuus on 3/7.

Harjoittele kysymyksiä kaltevuuskaavasta

Q1. Laske pisteiden (2, 3) ja (5, 7) läpi kulkevan suoran kaltevuus

Q2. Kun on annettu suoran yhtälö: y = 3x – 11, mikä on sen kaltevuus?

Q3. Jos suoran kaltevuus on 5/6 ja se kulkee pisteen (2, 5) kautta, mikä on suoran yhtälö kulmakertoimen leikkausmuodossa?

Q4. Laske suoran (0, -3) ja (1, 11) kanssa yhdensuuntaisen suoran kaltevuus

stdin c -ohjelmointi

Q5. Jos viivan kaltevuus on määrittelemätön, mitä voit päätellä viivasta?

Usein kysytyt kysymykset Slope Formulasta

Mikä on linjan kaltevuus?

Viivan kaltevuus on viivan jyrkkyyden tai kaltevuuden arvo x-y-tasossa. Kaltevuus lasketaan eri menetelmillä riippuen siitä, annetaanko suoran yhtälö vai viivan pisteiden koordinaatit.

Mikä on kaava tangentin kaavan kaltevuuden löytämiseksi?

Viivan kaltevuus lasketaan annetulla kaavalla. Oletetaan, että kahden suoralla sijaitsevan pisteen annetut koordinaatit ovat (x₁, ja₁)/(x_{2 ,}ja₂). Sitten kaava annetaan seuraavasti: Kaltevuus = m = tan θ = (y ₂ - ja ₁ )/(x ₂ – x ₁ )

Mikä on kaltevuuskaavan määritelmä?

Kaltevuuskaava määritellään seuraavasti,

• Kaltevuus = (muutos y-koordinaatissa)/(muutos x-koordinaatissa)
• Kaltevuus = nousu/juoksu.

Mikä on kaaviokaavan kaltevuus?

Viivan kaltevuus on sen kaltevuuden mitta positiivisella x-akselilla. Matemaattisesti kaltevuus määritellään seuraavasti nousta juoksun yli .