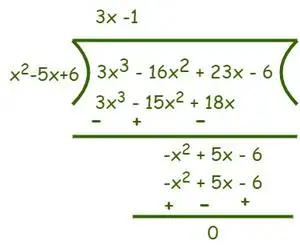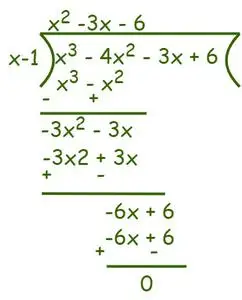Kuutio yhtälö on matemaattinen yhtälö, jossa 3-asteinen polynomi rinnastetaan vakioon tai toiseen polynomiin, jonka maksimiaste on 2. Kuutioyhtälön standardiesitys on kirves ³ +bx ² +cx+d = 0 jossa a, b, c ja d ovat reaalilukuja. Joitakin esimerkkejä kuutioyhtälöistä ovat x ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 jne.

Sisällysluettelo

• Polynomin määritelmä
• Yhtälön aste
• Kuutioyhtälön määritelmä
• Kuinka ratkaista kuutioyhtälöt?
• Kuutioyhtälöiden ratkaiseminen
• Kuutioyhtälön ratkaiseminen tekijöiden avulla
• Kuutioyhtälön ratkaiseminen graafisella menetelmällä
• Tehtäviä, jotka perustuvat kuutioyhtälöiden ratkaisemiseen
• Harjoittele tehtäviä kuutioyhtälöiden ratkaisemisessa

Oppiaksemme ratkaisemaan kuutioyhtälöitä meidän on ensin opittava polynomeista, polynomin asteesta ja muista. Tässä artikkelissa opimme polynomeista, polynomiyhtälöistä, kuutioyhtälöiden ratkaisemisesta tai kuutioyhtälöiden ratkaisemisesta ja muista yksityiskohtaisesti.

Polynomin määritelmä

Polynomi määritellään seuraavasti:

A polynomi on algebrallinen lauseke, jossa muuttujan potenssi on ei-negatiivinen kokonaisluku. Polynomin yleinen muoto on a₀xⁿ+ a₁x^n-1+ a₂x^n-2+… + a_n. Muuttujan maksimitehosta riippuen polynomi voidaan luokitella monomiaaliksi, binomiaaliksi, trinomiksi ja niin edelleen.

Mikä on yhtälö?

Yhtälö määritellään seuraavasti,

Yhtälö on polynomi, joka rinnastetaan numeeriseen arvoon tai mihin tahansa muuhun polynomiin. Esimerkiksi x + 2 on polynomi, mutta x + 2 = 5 on yhtälö. Vastaavasti 2x + 3 = x + 1 on myös yhtälö, kun taas 2x + 3 ja x + 1 ovat polynomeja erikseen.

Yhtälön aste

Yhtälön asteen määritelmä on esitetty alla:

Yhtälön aste määritellään yhtälön muuttujan suurimmaksi tehoksi.

Yhtälön asteen perusteella yhtälö voidaan luokitella seuraavasti:

• Lineaarinen yhtälö
• Toisen asteen yhtälö
• Kuutio yhtälö
• Bikvadraattinen yhtälö

Lineaarinen yhtälö

Yhtälöä, jossa muuttujan maksimiteho on 1, kutsutaan lineaariseksi yhtälöksi.

• Esimerkiksi 3x +1 = 0

Neliöllinen polynomi

Yhtälö, jossa muuttujan maksimiteho on 2, on toisen asteen yhtälö.

• Esimerkiksi 3x²+x+1 = 0

Kuutio yhtälö

Yhtälöä, jossa muuttujan maksimiteho on 3, kutsutaan kuutioyhtälöksi.

govinda näyttelijä

• Esimerkiksi 5x³+3x²+x+1 = 0

Bikvadraattinen polynomi

Yhtälöä, jossa muuttujan maksimiteho on 4, kutsutaan bikvadraattiseksi polynomiksi tai kvarttiseksi polynomiksi.

• Esimerkiksi 5x⁴+4x³+3x²+2x+1 = 0

Kuutioyhtälön määritelmä

Kuutio yhtälö on algebrallinen yhtälö, jossa polynomin korkein aste on 3. Jotkut esimerkit kuutioyhtälöistä ovat 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 jne.

Kuutioyhtälön yleinen muoto on,

kirves ³ + bx ² + cx + d = 0, a ≠ 0

Missä,

• a, b, ja c ovat muuttujan kertoimet ja niiden eksponenaatit ja d on vakio, ja
• a, b, c ja d ovat todellisia lukuja.

Kuinka ratkaista kuutioyhtälöt?

Kuutioyhtälö on yhtälö, jolla on aste kolme. Siinä on kolme ratkaisua, ja se voidaan ratkaista helposti seuraamalla alla lisättyjä vaiheita,

Vaihe 1: Etsi yksi ratkaisu kuutioyhtälöön osumalla ja kokeile menetelmää. Oletetaan, että meillä on kuutioyhtälö P(x), ja sitten löydetään mille tahansa x = a, P(a) = 0 ottamalla x = 0, ±1, ±2, ±3, … ja niin.

Vaihe 2: Kun saamme P(a) = 0, etsi P(x) tekijä (x – a)

Vaihe 3: Jaa P(x):llä (x – a), niin saat toisen asteen yhtälön sanomalla Q(x) polynomijakolla.

Vaihe 4: Factarisoi toisen asteen yhtälö Q(x) saadaksesi tekijät kuten (x – b) ja (x – c).

Vaihe 5: (x – a), (x – b) ja (x – c) ovat P(x):n tekijät ja ratkaisemalla jokainen tekijä saamme yhtälön juuret as, a, b ja c.

Lisätietoja aiheesta, Jakava polynomi

Kuutioyhtälöiden ratkaiseminen

A Kuutio yhtälö voidaan ratkaista kahdella tavalla

• pelkistämällä se toisen asteen yhtälöksi ja sitten ratkaisemalla se joko kertomalla tai toisen asteen kaavalla
• Graafisella menetelmällä

A Kuutio yhtälö on kolme juurta. Nämä juuret voivat olla todellisia tai kuvitteellisia. Siellä voi myös olla erillisiä juuria tai kaksi samaa ja yksi eri juuri ja kaikki kolme samaa juuria.

Huomaa, että jokaiselle yhtälölle, mukaan lukien Kuutioyhtälöt , yhtälö on aina järjestettävä vakiomuotoonsa ennen yhtälön ratkaisemista.

Esimerkiksi jos annettu yhtälö on 2x²-5 = x + 4/x, niin meidän on järjestettävä tämä uudelleen vakiomuotoonsa, eli 2x³-x²-5x-4 = 0. Nyt voimme ratkaista yhtälön millä tahansa sopivalla menetelmällä.

Kuutioyhtälön ratkaiseminen tekijöiden avulla

Kuutioyhtälön ratkaisu tekijälauseen avulla selitetään alla olevan esimerkin avulla,

Esimerkki: Etsi yhtälön f(x) = 3x juuret ³ -16x ² + 23x − 6 = 0.

Ratkaisu:

Annettu lauseke: f(x) = 3x³-16x²+ 23x − 6 = 0

Ensin kerroin polynomi saada juuret

Koska vakio on -6, mahdolliset tekijät ovat 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Sen mukaan tiedämme Tekijälause jos f(a) = 0, niin (x-a) on f(x)

Joten (x – 2) ja (x – 3) ovat f(x:n) kertoimia. Siksi (x – 2) ja (x – 3) tulo on myös tekijä f(x). Nyt jäljellä olevien tekijöiden löytämiseksi käytä pitkäjakomenetelmää ja jaa f(x) tuloilla (x – 2) ja (x – 3)

Näin ollen jakaja = (x – 2) (x – 3) = (x²– 5x + 6) ja osinko = 3x³-16x²+ 23x − 6. Jaa nyt alla olevan kuvan mukaisesti,

Jaon jälkeen saadaan (3x-1) osamääräksi ja jäännös on 0. Nyt kuten Jakoalgoritmi tiedämme sen Osinko = jakaja × osamäärä + jäännös.

⇒ f(x) = (3x³-16x²+ 23x − 6) = (x²– 5x + 6) (3x-1)

Koska f(x) = 0

⇒ (x²– 5x + 6) (3x-1) = 0

⇒ x²– 5x + 6 = 0 tai 3x-1 = 0

Nyt otetaan 3x-1 = 0 ⇒ x = 1/3, koska tiedämme jo kaksi juuria x:stä²– 5x + 6, jotka ovat 2 ja 3

Niin,

Annetun juuret Kuutio yhtälö ovat 1/3, 2 ja 3.

Kuutioyhtälön ratkaiseminen graafisella menetelmällä

Kuutioyhtälö ratkaistaan ​​graafisesti, kun annettua yhtälöä ei voi ratkaista muilla tekniikoilla. Joten tarvitsemme tarkan piirustuksen annetusta kuutioyhtälöstä. Yhtälön juuret ovat piste(t), joissa kuvaaja ylittää X-akselin, jos yhtälö on x:n ehdoissa ja jos yhtälö on y:n ehdoissa, yhtälön juuret ovat pisteet, joissa kuvaaja katkaisee Y-akselin.

Kuutioyhtälön todellisten ratkaisujen määrä on yhtä suuri kuin kuinka monta kertaa kuutioyhtälön kuvaaja ylittää X-akselin.

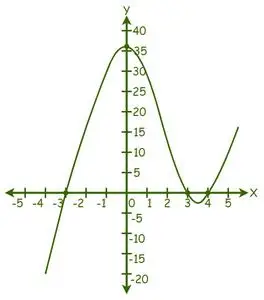
Esimerkki: Etsi yhtälön f(x) = x juuret ³ – 4x ² − 9x + 36 = 0, graafisella menetelmällä.

Ratkaisu:

Annettu lauseke: f(x) = x³– 4x²− 9x + 36 = 0.

Korvaa nyt vain satunnaiset arvot x:lle annetun funktion kaaviossa:

x	-4	-3	-2	-1	0	1 jos muuten lauseke javassa	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

Näemme, että kuvaaja on leikannut X-akselin 3 pisteestä, joten todellisia ratkaisuja on 3.

Kaavion ratkaisut ovat: x = -3, x = 3 ja x = 4.

Siksi annetun yhtälön juuret ovat -3, 3 ja 4.

Lue lisää,

• Lineaarinen yhtälö
• Neliöyhtälön ratkaiseminen
• Faktorointipolynomit

Tehtäviä, jotka perustuvat kuutioyhtälöiden ratkaisemiseen

Tehtävä 1: Etsi f(x) = x:n juuret ³ – 4x ² -3x + 6 = 0.

Ratkaisu:

Annettu lauseke: f(x) = x³– 4x²-3x + 6 = 0.

Ensin kerroin polynomi saada juuret.

Koska vakio on +6, mahdolliset tekijät ovat 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 - 144 -18 + 6 = -48 ≠ 0

Eli mukaan Tekijälause (x – 1) on annetun yhtälön tekijä. Nyt jäljellä olevien tekijöiden löytämiseksi käytä pitkäjakomenetelmää.

Mukaan Jakoalgoritmi voimme kirjoittaa,

Joten f(x) = x³– 4x²-3x + 6 = (x - 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 tai (x²– 3x – 6) = 0

Tiedämme, että toisen asteen yhtälön juuret ax²+ bx + c = 0 ovat,

x = [-b ± √(b²-4ac)]/2a

Siksi (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Näin ollen annetun kuutioyhtälön juuret ovat 1, (3+√33)/2 ja (3–√33)/2.

Tehtävä 2: Etsi yhtälön f(x) = 4x juuret ³ – 10x ² + 4x = 0.

Ratkaisu:

Annettu lauseke: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 tai 4x - 2 = 0, x - 2 = 0

⇒ x = 0 tai x = 1/2 tai x = 2

Näin ollen annetun yhtälön juuret ovat 0, 1/2 ja 2.

Tehtävä 3: Etsi yhtälön f(x) = x juuret ³ + 3x ² + x + 3 = 0.

Ratkaisu:

Annettu lauseke: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1 (x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 tai x²+1 = 0

mysql ainutlaatuinen avain

⇒ x = -3, ±i

Joten annetulla yhtälöllä on reaalijuuri, eli -3, ja kaksi imaginaarijuurta, eli ±i.

Tehtävä 4: Etsi yhtälön f(x) = x juuret ³ – 7x ² – x + 7 = 0.

Ratkaisu:

Annetut ilmaisut,

f(x) = x³– 3x²– 5x + 7 = 0

Ensin kerrotaan yhtälö, f(x): x³– 3x²– 5x + 7 = 0

Se voidaan laskea arvoon (x-7)(x+1)(x-1) = 0

Kun polynomi on otettu huomioon, voimme löytää juuret vertaamalla jokainen tekijä nollaan. Esimerkiksi:

• x – 7 = 0, joten x = 7
• x + 1 = 0, joten x = -1
• x – 1 = 0, joten x = 1

Joten yhtälön f(x) juuret: x³– 3x²– 5x + 7 = 0 are

• x = 7
• x = -1
• x = 1

Tehtävä 5: Etsi yhtälön f(x) = x juuret ³ – 6x ² + 11x − 6 = 0, graafisella menetelmällä.

Ratkaisu:

Annettu lauseke: f(x) = x³– 6x²+ 11x − 6 = 0.

Korvaa nyt vain satunnaiset arvot x:lle annetun funktion kaaviossa:

x	1	2	3	4	5
f(x)	0	0	0	6	24

Näemme, että kuvaaja on leikannut X-akselin 3 pisteestä, joten todellisia ratkaisuja on 3.

Kuvaajan ratkaisut ovat: x = 1, x = 2 ja x = 3.

Näin ollen annetun yhtälön juuret ovat 1, 2 ja 3.

Harjoittele tehtäviä kuutioyhtälöiden ratkaisemisessa

Alla on lisätty erilaisia ​​kuutioyhtälöihin liittyviä harjoitusongelmia. Ratkaise nämä ongelmat ymmärtääksesi täysin käsitteen Kuinka ratkaista kuutioyhtälö?

P1. Ratkaise kuutioyhtälö, 3x³+ 2x²– 11x + 7 = 0.

P2. Etsi kuutioyhtälön juuret, 4x³– 12x²+ 17 = 0.

P3. Ratkaise kuutioyhtälö, x³+ 4x²– x + 3 = 0 graafisella menetelmällä.

P4. Etsi numero, joka tyydyttää, -9x³+ 11x²– 8x + 2 = 0.

Usein kysyttyä kuutioyhtälöiden ratkaisemisesta

1. Mitä ovat kuutioyhtälöt?

Kuutioyhtälöt ovat algebrallisia yhtälöitä, joissa muuttujan maksimiteho on 3

2. Kuinka kerrotaan kuutioyhtälö?

Voimme kertoa kuutioyhtälön kahdella tavalla. Ensin ottamalla annetusta kuutioyhtälöstä yhteinen lineaarinen lauseke, niin meillä on tulona lineaarinen ja neliöllinen lauseke. Tämä toisen asteen yhtälö voidaan kertoa edelleen kaikkien tekijöiden saamiseksi. Toinen tapa on löytää nolla annetusta kuutioyhtälöstä asettamalla satunnaisia ​​arvoja. Arvo, jolle saamme yhtälön arvon nollaksi, on yksi annetun kuutioyhtälön nollia. Muodosta nyt tekijälauseen avulla lineaarinen lauseke, sanotaan x-a ja jaetaan annettu kuutioyhtälö tällä lausekkeella, joka antaa toisen asteen yhtälön osamääränä. Tämä saatu toisen asteen yhtälö voidaan kertoa edelleen kaikkien tekijöiden saamiseksi.

3. Kuinka ratkaiset kuutioyhtälön graafisesti?

Ratkaiseksesi kuutioyhtälön graafisesti laita x:n satunnaiset arvot annettuun kuutioyhtälöön ja ratkaise se, saat y:n arvot. Piirrä nämä saadut arvot kaavioon. Etsi koordinaatit, joissa kuvaaja leikkaa x-akselin. Nämä koordinaatit ovat kuutioyhtälön ratkaisu.

4. Voidaanko kaikki kuutioyhtälöt ratkaista tarkasti?

Jokaisella yhtälöllä, jolla on pariton voima, on oltava yksi todellinen juuri. Näin ollen kuutioyhtälöllä on oltava vähintään yksi todellinen juuri, toisin kuin toisen asteen yhtälössä, jossa molemmat juuret voivat olla kuvitteellisia, kun diskriminantti on pienempi kuin nolla.

5. Voiko kuutioyhtälöllä olla useita ratkaisuja?

Kyllä, kuutioyhtälöillä voi olla useita ratkaisuja, koska kuutioyhtälöllä voi olla jopa kolme erillistä reaalijuurta.

6. Mitä tarkoitat yhtälön asteella?

Yhtälön muuttujan suurinta tehoa kutsutaan polynomin asteeksi.

7. Mitä eroa on polynomin ja yhtälön välillä?

Polynomi on yksinkertaisesti algebrallinen yhtälö, jossa muuttujan potenssi on ei-negatiivinen kokonaisluku. Tätä polynomia, kun se rinnastetaan (=) numeeriseen arvoon tai toiseen polynomiin, sitä kutsutaan yhtälöksi.

8. Mikä on kuutioyhtälöiden kerroinlause?

Kerroinlause sanoo, että jos r on kuutioyhtälön ax juuri (ratkaisu)³+ bx²+ cx + d = 0, niin x – r on yhtälön tekijä.

9. Entä jos en löydä tarkkoja ratkaisuja kaavoilla?

Jos tarkkojen ratkaisujen löytäminen näyttää mahdottomalta, voimme käyttää numeerisia menetelmiä, kuten iteratiivisia menetelmiä (esim. Newtonin menetelmä) yhtälön juurten likimääräiseen arvioon.

Lisätietoja: Newton Raphsonin menetelmä .