Paraabelin vakiomuoto on y = ax2+ bx + c jossa a, b ja c ovat reaalilukuja ja a ei ole nolla. Paraabeli määritellään joukoksi kaikkia tason pisteitä, jotka ovat yhtä kaukana kiinteästä viivasta ja tason kiinteästä pisteestä.
Tässä artikkelissa ymmärrämme, mikä on paraabeli, paraabelin vakioyhtälö, siihen liittyvät esimerkit ja muut yksityiskohtaisesti.
Sisällysluettelo
Mikä on paraabeli?
Paraabeli on kartioleikkaus, joka määritellään joukoksi kaikkia pisteitä, jotka ovat yhtä kaukana pisteestä, jota kutsutaan polttopisteeksi, ja suorasta, jota kutsutaan suuntaviivaksi. Paraabelin standardiyhtälöt riippuvat sen suunnasta (avautumissuunnasta) ja sijainnista.
Paraabelin yhtälö
Paraabeliyhtälö voidaan kirjoittaa vakiomuotoon tai yleiseen muotoon ja molemmat on lisätty alle:
Paraabelin yleiset yhtälöt
Paraabelin yleinen yhtälö on,
y = 4a(x - h) 2 + k
(tai)
x = 4a(y – k) 2 + h
Missä (h, k) on paraabelin kärki.
Paraabelin standardiyhtälöt
Paraabelin standardiyhtälö on,
y = kirves 2 + bx + c
(tai)
x = on 2 + by + c
missä a ei voi koskaan olla nolla.
Paraabelin osat
Jotkut tärkeät termit ja paraabelin osat ovat:
- Painopiste: Tarkennus on paraabelin kiinteä piste.
- Suuntaviiva: Paraabelin suuntaviiva on viiva, joka on kohtisuorassa paraabelin akseliin nähden.
- Focal sointu: Painnetta, joka kulkee paraabelin keskipisteen läpi leikkaamalla paraabelin kahdessa eri kohdassa, kutsutaan polttojänteeksi.
- Polttoväli: Polttoväli on pisteen etäisyys (x1, ja1) paraabelissa tarkennuksesta.
- Oikea puoli: Latus rectum on polttojänne, joka kulkee paraabelin polttopisteen läpi ja on kohtisuorassa paraabelin akseliin nähden. Latus peräsuolen pituus on LL’ = 4a.
- Epäkeskisyys: Pisteen etäisyyden kohdistuksesta etäisyyteen suuntaviivasta kutsutaan epäkeskisyydeksi (e). Paraabelin epäkeskisyys on yhtä suuri kuin 1, eli e = 1.
Paraabelilla on neljä vakioyhtälöä, jotka perustuvat paraabelin ja sen akselin suuntaukseen. Jokaisella paraabelilla on erilainen poikittaisakseli ja konjugoitu akseli.
| Paraabelin yhtälö | Paraabeli | Paraabelin parametrien kaavat |
|---|---|---|
| ja 2 = 4ax | 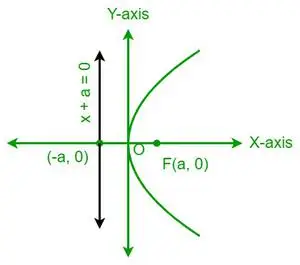 Vaakaparaabeli |
|
| ja 2 = -4ax |  Vaakaparaabeli |
|
| x 2 = 4ay |  Pystysuuntainen paraabeli |
|
| x 2 = -4ay |  Pystysuuntainen paraabeli |
|
Seuraavat ovat havainnot, jotka on tehty paraabelin yhtälöiden vakiomuodosta:
- Paraabeli on symmetrinen akselinsa suhteen. Esimerkiksi y2= 4ax on symmetrinen x-akselin suhteen, kun taas x2= 4ay on symmetrinen y-akselin suhteen.
- Jos paraabeli on symmetrinen x-akselin suhteen, paraabeli avautuu oikealle, jos x-kerroin on positiivinen, ja vasemmalle, jos x-kerroin on negatiivinen.
- Jos paraabeli on symmetrinen y-akselin suhteen, paraabeli avautuu ylöspäin, jos y-kerroin on positiivinen, ja alaspäin, jos y-kerroin on negatiivinen.
Seuraavat ovat paraabelin standardiyhtälöt, kun symmetria-akseli on joko yhdensuuntainen x- tai y-akselin kanssa ja kärki ei ole origossa.
| Paraabelin yhtälö | Paraabeli | Paraabelin parametrien kaavat |
|---|---|---|
| (ja – k)2= 4a(x – h) |  Vaakaparaabeli |
|
| (ja – k)2= -4a(x - h) |  Vaakaparaabeli |
|
| (x – h)2= 4a(y - k) |  Pysty paraabeli |
|
| (x – h)2= -4a(y - k) |  Pystysuuntainen paraabeli |
|
Paraabelijohdannaisen yhtälö
Olkoon P paraabelin piste, jonka koordinaatit ovat (x, y). Paraabelin määritelmän mukaan pisteen P etäisyys polttopisteeseen (F) on yhtä suuri kuin saman pisteen P etäisyys paraabelin suuntaviivaan. Tarkastellaan nyt suuntaviivan pistettä X, jonka koordinaatit ovat (-a, y).
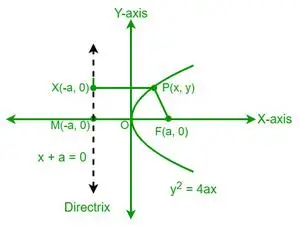
Paraabelin epäkeskisyyden määritelmästä saamme
e = PF/PX = 1
⇒ PF = PX
Tarkennuksen koordinaatit ovat (a, 0). Nyt koordinaattietäisyyskaavaa käyttämällä saadaan selville pisteen P (x, y) etäisyys fokukseen F (a, 0).
PF = √[(x – a)2+ (ja – 0)2]
⇒ PF = √[(x - a)2+ ja2] ------ (1)
Suuntaviivan yhtälö on x + a = 0. PX:n etäisyyden löytämiseksi käytämme kohtisuoran etäisyyskaavaa.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Tiedämme jo, että PF = PX. Eli yhtälöt (1) ja (2).
√[(x – a)2+ ja2] = (x + a)
Neliöimällä molemmilta puolilta saamme
⇒ [(x - a)2+ ja2] = (x + a)2
⇒ x2+ a2– 2ax + y2= x2+ a2+ 2ax
⇒ ja2– 2ax = 2ax
⇒ ja2= 2ax + 2ax ⇒ ja 2 = 4ax
Näin ollen olemme johtaneet paraabelin yhtälön. Samalla tavalla voimme johtaa kolmen muun paraabelin standardiyhtälöt.
- ja2= -4ax
- x2= 4ay
- x2= -4ay
ja 2 = 4ax ja 2 = -4ax, x 2 = 4ay ja x 2 = -4ay ovat paraabelin standardiyhtälöitä.
Parabolaan liittyvät artikkelit:
- Ympyrän yhtälö
- Ellipsin yhtälö
- Hyperbolan yhtälö
- Paraabelin sovellukset tosielämässä
Esimerkkejä paraabelin yhtälöstä
Esimerkki1: Etsi latuksen peräsuolen, fokuksen ja kärjen pituus, jos paraabelin yhtälö on y 2 = 12x.
Ratkaisu:
Annettu,
Paraabelin yhtälö on y2= 12x
Vertaamalla annettua yhtälöä vakiomuotoon y2= 4ax
4a = 12
⇒ a = 12/4 = 3
Tiedämme sen,
Paraabelin oikea puoli = 4a = 4 (3) = 12
Nyt paraabelin painopiste = (a, 0) = (3, 0)
Annetun paraabelin huippu = (0, 0)
Esimerkki 2: Etsi paraabelin yhtälö, joka on symmetrinen X-akselin suhteen ja kulkee pisteen (-4, 5) läpi.
Ratkaisu:
Annettu,
Paraabeli on symmetrinen X-akselin suhteen ja sen kärki on origossa.
Siten yhtälö voi olla muotoa y2= 4ax tai y2= -4ax, jossa merkki riippuu siitä, avautuuko paraabeli vasemmalle vai oikealle puolelle.
Paraabelin on avauduttava vasemmalle, koska se kulkee (-4, 5), joka sijaitsee toisessa kvadrantissa.
Joten yhtälö on: y2= -4ax
Korvaa (-4, 5) yllä olevassa yhtälössä,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Siksi paraabelin yhtälö on: y2= -4(25/16)x (tai) 4v2= -25x.
Esimerkki 3: Etsi paraabelin x fokuksen koordinaatit, akseli, suuntayhtälö ja latus rectum 2 = 16v.
Ratkaisu:
Annettu,
Paraabelin yhtälö on: x2= 16v
Vertaamalla annettua yhtälöä vakiomuotoon x2= 4ay,
4a = 16 ⇒ a = 4
Y:n kerroin on positiivinen, joten paraabeli avautuu ylöspäin.
Myös symmetria-akseli on positiivista Y-akselia pitkin.
Siten,
Paraabelin fokus on (a, 0) = (4, 0).
Suuntaviivan yhtälö on y = -a, eli y = -4 tai y + 4 = 0.
Peräsuolen latuksen pituus = 4a = 4(4) = 16.
Esimerkki 4: Etsi latuksen peräsuolen, fokuksen ja kärjen pituus, jos paraabelin yhtälö on 2(x-2) 2 + 16 = v.
Ratkaisu:
Annettu,
Paraabelin yhtälö on 2(x-2)2+ 16 = ja
Vertaamalla annettua yhtälöä paraabelin yleisyhtälöön y = a(x – h)2+ k, saamme
a = 2
(h, k) = (2, 16)
Tiedämme sen,
Paraabelin latus peräsuolen pituus = 4a
= 4(2) = 8
Nyt tarkennus = (a, 0) = (2, 0)
Nyt, Vertex = (2, 16)
Esimerkki 5: Paraabelin yhtälö on x 2 – 12x + 4y – 24 = 0, etsi sitten sen kärkipiste, fokus ja suunta.
Ratkaisu:
Annettu,
Paraabelin yhtälö on x2– 12x + 4v – 24 = 0
⇒ x2– 12x + 36 – 36 + 4v – 24 = 0
⇒ (x – 6)2+ 4v – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Saatu yhtälö on muodossa (x – h)2= -4a(y - k)
-4a = -4 ⇒ a = 1
Joten, kärki = (h, k) = (6, - 15)
Tarkennus = (h, k – a) = (6, -15-1) = (6, -16)
Suuntaviivan yhtälö on y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
Usein kysytyt kysymykset paraabelin yhtälöstä
Kuinka löydät paraabelin vakioyhtälön?
Paraabelin vakiomuoto on y2= 4ax tai x2= 4ay.
Mikä on paraabelin normaaliyhtälö?
Normaalin yhtälö paraabelille y2= 4ax, jonka kaltevuus on m, annetaan seuraavasti: y = mx – 2am – am 3
Kuinka löydät paraabelin huippupisteen?
Annetulle paraabelille: y = ax2+ bx + c sen kärkipiste löytyy kaavalla x = − b/2a. Kytke tämä x-arvo takaisin yhtälöön löytääksesi vastaavan y-koordinaatin.
min max
