Kitka on suhteellista liikettä vastustavaa voimaa ja sitä esiintyy kappaleiden välisessä rajapinnassa, mutta myös kappaleiden sisällä, kuten nesteiden tapauksessa. Kitkakertoimen käsitteen muotoili ensimmäisenä Leonardo da Vinci. Kitkakertoimen suuruus määräytyy pintojen ominaisuuksien, ympäristön, pinnan ominaisuuksien, voiteluaineen jne. mukaan.
Kitkan lait
Kitkalakia on viisi ja ne ovat:
• Liikkuvan kohteen kitka on verrannollinen ja kohtisuorassa normaalivoimaan nähden.
• Kohteen kokema kitka riippuu sen pinnan luonteesta, jonka kanssa se on kosketuksissa.
• Kitka on riippumaton kosketusalueesta niin kauan kuin kosketusaluetta on.
• Kineettinen kitka on riippumaton nopeudesta.
• Staattinen kitkakerroin on suurempi kuin kineettinen kitkakerroin.
Kun näemme minkä tahansa kohteen, voimme nähdä sen sileän pinnan, mutta kun samaa kohdetta tarkastellaan mikroskoopilla, voidaan nähdä, että jopa sileänä näyttävällä esineellä on karkeita reunoja. Pienet kukkulat ja urat näkyvät mikroskoopin läpi, ja ne tunnetaan pinnan epätasaisuuksina. Joten kun yhtä esinettä siirretään toisen päälle, nämä pinnan epäsäännöllisyydet sotkeutuvat aiheuttaen kitkaa. Mitä enemmän karheutta, sitä enemmän epäsäännöllisyyksiä ja suurempi on käytetty voima.
Staattinen kitka
Staattisen kitkan syistä on useita teorioita, ja kuten useimmat kitkaan liittyvät käsitteet, jokainen niistä osoittautuu päteväksi joissakin olosuhteissa, mutta epäonnistuu muissa olosuhteissa. Tosielämän sovelluksiin (erityisesti teollisuuskoneisiin ja liikenteeseen liittyviin). Hallitse kahta yleisimmin hyväksyttyä staattisen kitkan teoriaa, jotka liittyvät pintojen mikroskooppiseen karheuteen.
Huolimatta siitä, kuinka täydellisesti pinta on koneistettu, viimeistelty ja puhdistettu, siinä on väistämättä epätasaisuuksia – pääasiassa karheutta, joka koostuu huipuista ja laaksoista, aivan kuten vuoristossa. (Teknisesti huiput ovat epätasaisuuksia.) Kun kaksi pintaa ovat kosketuksissa, voi vaikuttaa siltä, että niillä on suuri, tarkasti määritelty kosketusalue, mutta todellisuudessa kosketus tapahtuu vain tietyissä paikoissa – eli missä molemmat pinnat häiritsevät.
Näiden pienten asperiteettien välisten kosketusalueiden summaa kutsutaan todelliseksi tai tehokkaaksi kosketusalueeksi. Koska nämä yksittäiset kosketusalueet ovat hyvin pieniä, pintojen välinen paine (paine = voima ÷ pinta-ala) näissä kohdissa on erittäin korkea. Tämä äärimmäinen paine mahdollistaa pintojen välisen tartunnan kylmähitsauksena tunnetun prosessin kautta, joka tapahtuu molekyylitasolla. Ennen kuin pinnat voivat liikkua suhteessa toisiinsa, tämän tartunnan aiheuttavat sidokset on katkettava.
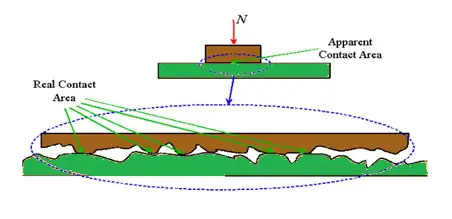
Lisäksi pintojen karheus merkitsee sitä, että joissakin paikoissa toisen pinnan epätasaisuudet asettuvat toisen pinnan laaksoihin eli pinnat lukkiutuvat toisiinsa.
Nämä lukitut alueet on murrettava tai plastisesti muotoiltu ennen kuin pinnat voivat liikkua. Toisin sanoen kulumista täytyy tapahtua. Joten useimmissa sovelluksissa staattinen kitka johtuu sekä kosketuspintojen tarttumisesta että kulumisesta.
Staattisen kitkan lait
On olemassa kaksi staattisen kitkan lakia:
- Ensimmäinen laki: Staattisen kitkan maksimivoima ei riipu kosketusalueesta.
- Toinen laki: Staattisen kitkan maksimivoima on verrattavissa normaalivoimaan, eli jos normaalivoima kasvaa, kasvaa myös suurin ulkoinen voima, jonka kohde voi kestää liikkumatta.

Staattisen kitkan kaavan derivointi
Tarkastellaan mg:n painoista lohkoa, joka makaa vaakasuoralla pinnalla kuvan osoittamalla tavalla. Kun kappale painaa pintaa vasten, pinta muotoutuu, vaikka se näyttäisi olevan jäykkä. Epämuodostunut pinta työntää kappaletta normaalilla voimalla R, joka on kohtisuorassa pintaan nähden. Tätä kutsutaan normaaliksi reaktiovoimaksi. Se tasapainottaa mg eli
R = mg
Tarkastellaan nyt, että lohkoon kohdistuu voima P. Selvästi keho pysyy levossa, koska jokin muu voima F vaikuttaa vaakasuunnassa ja vastustaa kohdistettua voimaa P, jolloin kehoon kohdistuva nettovoima nolla. Tätä voimaa F, joka vaikuttaa pitkin kappaleen pintaa kosketuksessa pöydän pintaan, kutsutaan kitkavoimaksi.
Niin kauan kuin keho ei liiku F = P. Tämä tarkoittaa, että jos lisäämme P:tä, myös kitka F kasvaa pysyen aina yhtä suurena kuin P.
Tämä kitkavoima, joka tulee voimaan, kunnes varsinainen liike on alkanut, tunnetaan staattisena kitkana.
Staattisen kitkan kerroin
Staattinen kitka on kitkaa, joka syntyy, kun esine asetetaan pinnalle. Ja kineettinen kitka johtuu esineen liikkeestä pinnalla. Kitka on hyvin karakterisoitu kitkakertoimella ja se selitetään kitkavoiman ja normaalivoiman välisenä suhteena. Tämä auttaa esinettä makaamaan pinnalla. Staattinen kitkakerroin on skalaarisuure ja sitä merkitään μ:näs.
Staattisen kitkakertoimen kaava ilmaistaan seuraavasti
mu_{s} = frac{F}{N} Missä
m s = staattinen kitkakerroin
F = staattinen kitkavoima
N = normaali voima

Kineettinen kitka
Kineettinen kitka määritellään voimaksi, joka vaikuttaa liikkuvien pintojen väliin. Pinnalla liikkuva kappale kokee voiman vastakkaiseen suuntaan kuin sen liike. Voiman suuruus riippuu näiden kahden materiaalin välisestä kineettisestä kitkakertoimesta.
Kitka määritellään helposti voimaksi, joka estää liukuvaa esinettä. Kineettinen kitka on osa kaikkea ja se häiritsee kahden tai useamman esineen liikettä. Voima vaikuttaa vastakkaiseen suuntaan kuin tapa, jolla esine haluaa liukua.
Jos auton on pysähdyttävä, jarrutamme ja juuri siinä kitka tulee esiin. Kun kävellessä haluaa yhtäkkiä pysähtyä, kitka on taas kiittää. Mutta kun meidän on pysähdyttävä keskellä lätäköä, asiat vaikeutuvat, koska kitkaa on vähemmän, eikä se voi auttaa sitä niin paljon.

Kahden pinnan välisen staattisen kitkan voittaminen poistaa olennaisesti sekä molekyyliesteet (kylmähitsaus asperiteettien välillä) että jossain määrin mekaaniset esteet (pintojen aukkojen ja laaksojen välinen häiriö) liikkeeltä. Kun liike on aloitettu, jonkin verran kulumista tapahtuu edelleen, mutta paljon alhaisemmalla tasolla kuin staattisen kitkan aikana ja pintojen välinen suhteellinen nopeus ei anna riittävästi aikaa lisäkylmähitsauksen suorittamiseen (paitsi erittäin alhaisen nopeuden tapauksessa).
Kun suurin osa adheesiosta ja hankauksesta voitetaan liikkeen aikaansaamiseksi, pintojen välinen liikkeen vastus vähenee ja pinnat liikkuvat nyt kineettisen kitkan vaikutuksesta, joka on paljon pienempi kuin staattinen kitka.
Kineettisen kitkan lait
Kineettisellä kitkalla on neljä lakia:
- Ensimmäinen laki: Kineettisen kitkan voima (Fk) on suoraan verrannollinen normaaliin reaktioon (N) kahden kosketuksissa olevan pinnan välillä. Missä, m k = vakio, jota kutsutaan kineettiseksi kitkakertoimeksi.
- Toinen laki: Kineettinen kitkavoima on riippumaton kosketuksissa olevien pintojen muodosta ja näennäisalueesta.
- Kolmas laki: Se riippuu kosketuksissa olevan pinnan luonteesta ja materiaalista.
- Neljäs laki: Se on riippumaton kosketuksissa olevan kohteen nopeudesta, jos kohteen ja pinnan välinen suhteellinen nopeus ei ole liian suuri.

Kineettisen kitkan kaava
Kineettinen kitkakerroin on merkitty kreikkalaisella kirjaimella mu ( m ), alaindeksillä k. Kineettisen kitkan voima on m k kertaa kehoon kohdistuva normaali voima. Se ilmaistaan Newtonina (N).
Kineettinen kitkayhtälö voidaan kirjoittaa seuraavasti:
Kineettinen kitkavoima = (kineettinen kitkakerroin) (normaali voima)
F k = m k h
Missä,
F k = kineettinen kitkavoima
m k kineettinen kitkakerroin
h = normaali voima (kreikkalainen kirjain eta)

Kineettisen kitkan kaavan johdannainen
Tarkastellaanpa painolohkoa mg makaa vaakasuoralla pinnalla kuvan osoittamalla tavalla. Kun kappale painaa pintaa vasten, pinta muotoutuu, vaikka se näyttäisi olevan jäykkä. Epämuodostunut pinta työntää kehoa normaalilla voimalla R joka on kohtisuorassa pintaan nähden. Tätä kutsutaan normaaliksi reaktiovoimaksi. Se tasapainottaa mg eli R = mg .
b plus puu
Ajatellaanpa sitä nyt voimana P levitetään lohkoon kuvan mukaisesti. Ilmeisesti keho pysyy levossa jonkin muun voiman takia F tulee peliin vaakasuunnassa ja vastustaa kohdistettua voimaa P tuloksena kehoon kohdistuva nettovoima nolla. Tätä voimaa F, joka vaikuttaa pitkin kappaleen pintaa kosketuksessa pöydän pintaan, kutsutaan kitkavoima .
Niin kauan kuin vartalo ei liiku F = P . Tämä tarkoittaa, että jos lisäämme P:tä, myös kitka F kasvaa pysyen aina yhtä suurena kuin P.
Kun lisäämme käytettyä voimaa hieman rajoittavan kitkan yläpuolelle, varsinainen liike alkaa. Tämä ei tarkoita, että kitka olisi kadonnut. Se tarkoittaa vain, että voima on voittanut rajoittavan kitkan. Tämä kitkavoima tässä vaiheessa tunnetaan nimellä kineettinen kitka tai dynaaminen kitka.
Kineettinen kitka tai dynaaminen kitka on vastakkainen voima, joka tulee peliin, kun keho itse asiassa liikkuu toisen kehon pinnan yli.
Staattisen ja kineettisen kitkan soveltaminen

Staattisen kitkan sovellukset
Joitakin tosielämän esimerkkejä staattisesta kitkasta on annettu alla olevissa kohdissa:
- Paperit pöydällä
- Telineessä roikkuva pyyhe
- Kirjanmerkki kirjassa
- Auto pysäköity mäkeen
Kineettisen kitkan sovellukset
Joitakin tosielämän esimerkkejä kineettisestä kitkasta on annettu alla olevissa kohdissa.
- Kitkalla on valtava rooli myös jokapäiväisissä tapahtumissa, kuten kahden esineen hankautuessa. Tuloksena oleva liike muuttuu lämmöksi ja johtaa siten tulipaloon joissakin tapauksissa.
- Se vastaa myös kulumisesta ja siksi tarvitsemme öljyä koneen osien voiteluun, koska se vähentää kitkaa.
- Kun kahta esinettä hierotaan toisiaan vasten, kitkavoima muuttuu lämpöenergiaksi, joka harvoissa tapauksissa aiheuttaa tulipalon
- Kineettinen kitka on vastuussa koneen osien kulumisesta, joten on tärkeää voidella koneen osat öljyllä.
Ero staattisen ja kineettisen kitkan välillä
| Staattinen kitka | Kineettinen kitka |
| Staattinen kitka on kitka kahden tai useamman kohteen välillä, jotka eivät liiku toisiinsa nähden | Kineettinen kitka on kitka kahden tai useamman toisiinsa nähden liikkeessä olevan kohteen välillä. |
| Staattisen kitkan suuruus on suurempi johtuen sen kertoimen suuremmasta arvosta. | Kineettisen kitkan suuruus on verrattain pienempi johtuen sen kertoimen alhaisesta arvosta. |
Staattista kitkaa kuvaava yhtälö on annettu kaavalla Fs= msh | Kineettistä kitkaa kuvaava yhtälö on annettu kaavalla Fk= mkh |
| Sen arvo voi olla nolla. | Sen arvo ei voi koskaan olla nolla. |
| Esimerkki - lyijykynä pöydällä. | Esimerkki - kynän siirtäminen pöydän yli. |
Staattiseen ja kineettiseen kitkaan perustuvat esimerkkitehtävät
Kysymys 1: Mies työntää suurta, 75,0 kg painavaa pahvia lattialla.
Ratkaisu:
Kineettinen kitkakerroin on μk= 0,520
Työntekijä kohdistaa eteenpäin 400,0 N voimaa.
Mikä on kitkavoiman suuruus?
Vastaus: Tasaisella pinnalla kappaleen normaalivoima saadaan selville kaavalla
h = mg
Korvaamalla η:n arvo yhtälössä Fk= mkη, saamme
Fk= (0,520) (75,0 kg) (9,80 m/s2) = 382,2N
Kysymys 2: Laske yllä olevassa kysymyksessä laatikkoa liikuttava nettovoima?
Ratkaisu:
Kehoon vaikuttava nettovoima on kaikkien kehoon vaikuttavien voimien summa.
Tässä tapauksessa kehoon vaikuttavat voimat ovat ihmisen kohdistama voima ja vastakkaiseen suuntaan vaikuttava kineettinen kitka.
Jos eteenpäin suuntautuvaa liikettä pidetään positiivisena, nettovoima lasketaan seuraavasti:
Fnetto= Ftyöntekijä– Fk
Korvaamalla yllä olevan yhtälön arvot, saamme
Fnetto= 400 N – 382,2 N = 17,8 N
Kysymys 3: Miksi rullaavassa liikkeessä esiintyy kitkaa?
Vastaus:
Teoriassa pallo koskettaa pintaa.
Mutta todellisuudessa pallo (ja/tai pinta) vääntyy kuormituksen vaikutuksesta ja kosketusalue muuttuu elliptiseksi.
Teoriassa vierintäpintojen, kuten useimmissa pyörivissä ja lineaarisissa laakereissa (lukuun ottamatta liukulaakereita), ei pitäisi kohdata kitkavoimia.
Mutta tosielämän sovelluksissa kolme tekijää aiheuttaa kitkaa vierintäpinnoissa:
1. Mikroliukutus pintojen välillä (pinnat liukuvat toisiinsa nähden)
2. Materiaalien joustamattomat ominaisuudet (eli muodonmuutos).
3. Pintojen epätasaisuus
Kysymys 4: 10 kg painava esine asetetaan tasaiselle pinnalle. Staattinen kitka näiden kahden pinnan välillä on annettu 15 N:nä. Löytäkää staattisen kitkakerroin?
Ratkaisu:
Annettu
m = 10 kg
F = 15 N
ms= ?
Tiedämme sen,
Normaalivoima, N = mg
Joten N = 10 × 9,81 = 98,1 N
Staattisen kitkakertoimen kaava on
ms= 15/N
kuinka tulostaa javams= 15/98,1
m s = 0,153
Kysymys 5: Esineen normaalivoima ja staattinen kitkavoima ovat vastaavasti 50 N ja 80 N. Löytää staattisen kitkakertoimen?
Ratkaisu:
Annettu
N = 50 N
F = 80 N ja μs= ?
Staattisen kitkakertoimen kaava on
ms= F/N
ms= 80/50
ms= 1,6
Kysymys 6: Mikä on staattisen ja kineettisen kitkan välinen suhde?
Vastaus:
Staattisen kitkan voima pitää paikallaan olevan kohteen levossa. Kun staattisen kitkan voima on voitettu, kineettisen kitkan voima hidastaa liikkuvaa kohdetta.
Kysymys 7: Jääkaappi painaa 1619 N ja staattinen kitkakerroin on 0,50. Mitä voimaa käytetään vähiten jääkaapin siirtämiseen?
Ratkaisu:
Annetut tiedot:
Jääkaapin paino, W=1619 N
W = 1619 N
Staattinen kitkakerroin, μs= 0,50
Jääkaapin siirtämiseen tarvittava vähimmäisvoima voidaan antaa seuraavasti:
F = msSISÄÄN
F = 0,50 × 1619
F = 809,50 N.
