Strongly Connected Components (SCC:t) ovat graafiteorian ja algoritmien peruskäsite. Suunnatussa kaaviossa a Vahvasti yhdistetty komponentti on kärkien osajoukko, jossa jokainen osajoukon kärkipiste on saavutettavissa jokaisesta toisesta saman osajoukon kärjestä kulkemalla suunnattujen reunojen läpi. Löytäminen SCC:t kaavio voi tarjota tärkeitä näkemyksiä graafin rakenteesta ja liitettävyydestä erilaisilla sovelluksilla, kuten sosiaalisten verkostojen analysointi, verkkoindeksointi ja verkon reititys . Tämä opetusohjelma tutkii määritelmiä, ominaisuuksia ja tehokkaita algoritmeja vahvasti toisiinsa liittyvien komponenttien tunnistamiseen graafin tietorakenteissa

upcasting

Sisällysluettelo

• Mikä on Strongly Connected Components (SCC)?
• Miksi vahvasti yhdistetyt komponentit (SCC) ovat tärkeitä?
• Ero yhdistettyjen ja vahvasti kytkettyjen komponenttien (SCC) välillä
• Miksi perinteistä DFS-menetelmää ei voida käyttää vahvasti kytkettyjen komponenttien löytämiseen?
• Kahden vahvasti yhteydessä olevan komponentin yhdistäminen yksisuuntaisella reunalla
• Raaka voima -menetelmä vahvasti toisiinsa liittyvien komponenttien löytämiseen
• Tehokas tapa löytää vahvasti toisiinsa yhteydessä olevia komponentteja (SCC)
• 1. Kosarajun algoritmi:
• 2. Tarjan’s Algorithm:
• Johtopäätös

Mikä on Strongly Connected Components (SCC)?

A vahvasti kytketty komponentti suunnatun graafin on maksimaalinen aligraafi, jossa jokainen pistepari on saavutettavissa keskenään. Tämä tarkoittaa, että kahdelle tämän aligraafin solmulle A ja B on polku A:sta B:hen ja polku B:stä A:hen.

Esimerkiksi: Alla olevassa kaaviossa on kaksi vahvasti yhteydessä olevaa komponenttia {1,2,3,4} ja {5,6,7}, koska jokaisesta kärjestä on polku jokaiseen toiseen kärkeen samassa vahvasti yhteydessä olevassa komponentissa.

Vahvasti yhdistetty komponentti

Miksi vahvasti yhdistetyt komponentit (SCC) ovat tärkeitä?

SCC:n ymmärtäminen on ratkaisevan tärkeää eri sovelluksissa, kuten:

• Verkko-analyysi : Tunnistaa tiiviisti toisiinsa liittyvien solmujen klusterit.
• Verkkoindeksointirobottien optimointi : Verkkokaavion osien määrittäminen, jotka liittyvät läheisesti toisiinsa.
• Riippuvuuden resoluutio : Ohjelmistossa sen ymmärtäminen, mitkä moduulit ovat toisistaan ​​riippuvaisia.

Ero yhdistettyjen ja vahvasti kytkettyjen komponenttien välillä ( SCC:t)

Liitettävyys a suuntaamaton graafi viittaa siihen, ovatko kaksi kärkeä tavoitettavissa toisistaan ​​vai eivät. Kahden kärjen sanotaan olevan yhteydessä toisiinsa, jos niiden välillä on polku. sillä välin Vahvasti yhdistetty koskee vain suunnatut kaaviot . Suunnatun graafin aligraafia pidetään an Vahvasti yhdistetyt komponentit (SCC) jos ja vain jos jokaiselle kärkiparille A ja B , on olemassa polku A to B ja polku sieltä B to A . Katsotaan miksi tavallinen dfs-menetelmä yhdistettyjen komponenttien etsimiseen kuvaajaa ei voida käyttää vahvasti toisiinsa liittyvien komponenttien määrittämiseen.

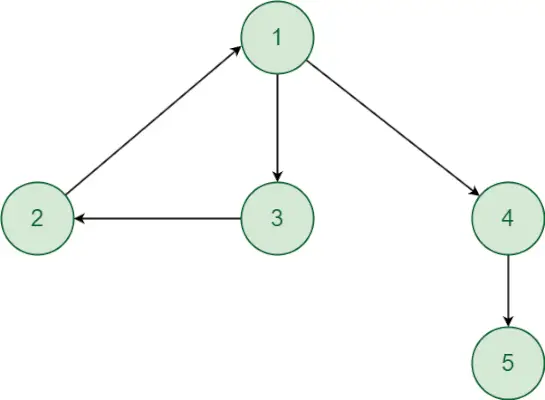
Harkitse seuraavaa kaaviota:

Aloitetaan nyt a dfs kutsu pisteestä 1 vieraillaksesi muissa pisteissä.

Miksi perinteistä DFS-menetelmää ei voida käyttää vahvasti kytkettyjen komponenttien löytämiseen?

Kaikki kärjet ovat saavutettavissa kärjestä 1. Mutta kärjet 1 ja 5,6,7 eivät voi olla samassa vahvasti yhteydessä olevassa komponentissa, koska pisteestä 5,6 tai 7 ei ole suunnattua polkua kärkeen 1. Graafilla on kaksi vahvasti yhdistetyt komponentit {1,2,3,4} ja {5,6,7}. Joten perinteistä dfs-menetelmää ei voida käyttää vahvasti toisiinsa liittyvien komponenttien löytämiseen.

poistamalla viimeinen commit git

Kahden vahvasti yhteydessä olevan komponentin yhdistäminen yksisuuntaisella reunalla

Kahdesta eri yhdistetystä komponentista tulee yksi komponentti, jos yhdestä komponentista toisen komponentin kärjen väliin lisätään reuna. Mutta näin ei ole vahvasti kytkettyjen komponenttien kohdalla. Kahdesta vahvasti kytketystä komponentista ei tule yhtä vahvasti kytkettyä komponenttia, jos yhdestä SCC:stä toiseen SCC:hen on vain yksisuuntainen reuna.

osavaltioiden luettelo

Raaka voima -menetelmä vahvasti toisiinsa liittyvien komponenttien löytämiseen

Yksinkertaisena menetelmänä on, että jokaiselle pisteelle i (joka ei ole osa mitään vahvasti komponenttia) etsitään kärjet, jotka ovat osa vahvasti yhdistetystä komponentista, joka sisältää kärjen i. Kaksi kärkeä i ja j ovat samassa vahvasti yhteydessä olevassa komponentissa, jos niillä on suunnattu polku kärjestä i kärkeen j ja päinvastoin.

Ymmärretään lähestymistapaa seuraavan esimerkin avulla:

• Alkaen kärjestä 1. Huipusta 1 on polku kärkeen 2 ja päinvastoin. Vastaavasti on olemassa polku kärjestä 1 kärkeen 3 ja päinvastoin. Joten kärki 2 ja 3 ovat samassa vahvasti yhteydessä komponentissa kuin kärki 1. Vaikka kärjestä 1 on suunnattu polku kärkeen 4 ja kärkeen 5. Mutta kärjestä 4,5 kärkeen 1 ei ole suunnattua polkua, joten kärki 4 ja 5 eivät ole samassa vahvasti yhteydessä olevassa komponentissa kuin kärki 1. Siten Vertex 1,2 ja 3 muodostavat vahvasti yhdistetyn komponentin.
• Vertex 2:lle ja 3:lle vahvasti yhdistetty komponentti on jo määritetty.
• Vertex 4:ssä on polku kärjestä 4 kärkeen 5, mutta kärjestä 5 kärkeen 4 ei ole polkua. Joten pisteet 4 ja 5 eivät ole samassa vahvasti yhteydessä olevassa komponentissa. Joten sekä Vertex 4 että Vertex 5 ovat osa Single Strongly Connected Component -komponenttia.
• Tästä syystä tulee 3 vahvasti yhdistettyä komponenttia {1,2,3}, {4} ja {5}.

Alla on yllä olevan lähestymistavan toteutus:

#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vektori & vis) { // Jos curr-solmu on kohde return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Selvittää onko polku lähteestä // kohde bool isPath(int src, int des, vektori>& adj) { vektori vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funktio palauttaa kaikki graafin vahvasti liittyvät // komponentit.  vektori> etsiSCC(int n, vektori>& a) { // Tallentaa kaikki vahvasti kytketyt komponentit.  vektori> ans;  // Tallentaa onko kärki osa jotakin vahvasti // yhdistetty komponenttivektoria is_scc(n + 1, 0);  vektori> adj(n + 1);  for (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> reunat{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vektori> ans = obj.findSCC(V, reunat);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>

import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, lista vis) { // Jos curr-solmu on kohde return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Selvittää onko polku lähteestä // kohde looginen isPath(int src, int des, List> adj) { List vis = new ArrayList(adj.size() + 1);  for (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> findSCC(int n, List> a) { // Tallentaa kaikki vahvasti kytketyt komponentit.  Lista> ans = new ArrayList();  // Tallentaa, onko huippupiste osa vahvasti // yhdistettyjen komponenttien luetteloa is_scc = uusi ArrayList(n + 1);  for (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = new ArrayList();  for (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List reuna : a) { adj.get(reuna.get(0)).add(reuna.get(1));  } // Kaikkien pisteiden läpikulku (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = uusi ArrayList();  scc.add(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> reunat = new ArrayList();  edges.add(new ArrayList(List.of(1, 3)));  edges.add(new ArrayList(List.of(1, 4)));  edges.add(new ArrayList(Lista.of(2, 1)));  edges.add(new ArrayList(Lista.of(3, 2)));  edges.add(new ArrayList(Lista.of(4, 5)));  Lista> ans = obj.findSCC(V, reunat);  System.out.println('Vahvasti yhdistetyt komponentit ovat:');  varten (Lista x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Tämän koodin tarjoaa shivamgupta310570>>Python

using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, lista vis) { // Jos curr-solmu on kohde, return true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Selvittää onko polku lähteestä kohteeseen public bool IsPath(int src, int des, List> adj) { var show = uusi luettelo (adj.Count + 1);  for (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> EtsiSCC(int n, List> a) { // Tallentaa kaikki vahvasti kytketyt komponentit var ans = new List>();  // Tallentaa, onko kärki osa jotakin vahvasti yhdistettyä komponenttia var isScc = new List (n + 1);  for (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  for (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } for (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  for (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> reunat = uusi lista> { uusi luettelo { 1, 3 }, uusi luettelo { 1, 4 }, uusi luettelo { 2, 1 }, uusi luettelo { 3, 2 }, uusi luettelo { 4, 5 } };  Lista> ans = obj.EtsiSCC(V, reunat);  Console.WriteLine('Vahvasti yhdistetyt komponentit ovat:');  foreach (muuttuja x ansissa) { foreach (muuttuja y x:ssä) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Tämän koodin tarjoaa shivamgupta310570>>Javascript

Strongly Connected Components are: 1 2 3 4 5>

Aika monimutkaisuus: O(n * (n + m)), koska jokaisen kärkiparin kohdalla tarkistamme, onko niiden välillä polku.
Aputila: O(N)

123moviesin kaltaiset elokuvasivustot

Tehokas tapa löytää vahvasti toisiinsa yhteydessä olevia komponentteja (SCC)

SCC:iden löytämiseksi kaaviosta voimme käyttää algoritmeja, kuten Kosarajun algoritmi tai Tarjan’s Algorithm . Tutkitaan näitä algoritmeja askel askeleelta.

1. Kosarajun algoritmi :

Kosarajun algoritmi sisältää kaksi päävaihetta:

1. Suoritetaan Depth-First Search (DFS) alkuperäisessä kaaviossa :
   • Teemme ensin DFS:n alkuperäiselle kuvaajalle ja tallennamme solmujen lopetusajat (eli ajan, jolloin DFS lopettaa solmun tutkimisen kokonaan).
2. DFS:n suorittaminen transponoidulle kuvaajalle :
   • Tämän jälkeen käännämme kaavion kaikkien reunojen suunnan päinvastaiseksi luodaksemme transponoidun graafin.
   • Seuraavaksi suoritamme DFS:n transponoidulle graafille ottaen huomioon solmut alenevassa järjestyksessä niiden ensimmäisessä vaiheessa tallennettujen lopetusaikojen mukaan.
   • Jokainen DFS-läpikäynti tässä vaiheessa antaa meille yhden SCC:n.

Tässä on yksinkertaistettu versio Kosarajun algoritmista:

1. DFS alkuperäisessä kaaviossa : Record lopetusajat.
2. Transponoi kaavio : Käännä kaikki reunat taaksepäin.
3. DFS transponoidussa kaaviossa : Käsittele solmut lyhentävien lopetusaikojen mukaan SCC:iden löytämiseksi.

2. Tarjan’s Algorithm :

Tarjanin algoritmi on tehokkaampi, koska se löytää SCC:t yhdestä DFS-kierrosta käyttämällä pinoa ja lisäkirjanpitoa:

1. DFS Traversal : Säilytä DFS:n aikana indeksi jokaiselle solmulle ja pienin indeksi (matalan linkin arvo), joka solmusta voidaan saavuttaa.
2. Pino : Seuraa tällä hetkellä rekursiopinossa olevia solmuja (osa nykyisestä SCC:stä tutkitaan).
3. SCC:iden tunnistaminen : Kun solmun matalan linkin arvo on yhtä suuri kuin sen indeksi, se tarkoittaa, että olemme löytäneet SCC:n. Pop kaikki solmut pinosta, kunnes saavutamme nykyisen solmun.

Tässä on yksinkertaistettu hahmotelma Tarjanin algoritmista:

1. Alustaaindex>0:ksi.
2. Suorita DFS jokaiselle vierailemattomalle solmulle.
   • Aseta solmun indeksi ja matalan linkin arvo.
   • Työnnä solmu pinoon.
   • Suorita kullekin viereiselle solmulle DFS, jos siinä ei käyty, tai päivitä matalan linkin arvo, jos se on pinossa.
   • Jos solmun matalan linkin arvo on yhtä suuri kuin sen indeksi, nosta solmut pinosta muodostamaan SCC.

Johtopäätös

Ymmärtäminen ja löytäminen vahvasti kytketyt komponentit suunnatussa graafissa on olennainen monille tietojenkäsittelytieteen sovelluksille. Kosarajun ja Tarjan’s Algoritmit ovat tehokkaita tapoja tunnistaa SCC:t, joilla jokaisella on oma lähestymistapansa ja etunsa. Hallitsemalla nämä käsitteet voit paremmin analysoida ja optimoida monimutkaisten verkkojen rakennetta ja käyttäytymistä.