Tässä artikkelissa käsittelemme puun läpikulkua tietorakenteessa. Termi 'puun läpikulku' tarkoittaa puun jokaisen solmun läpi kulkemista tai vierailua. Lineaarista tietorakennetta, kuten linkitetty luettelo, jono ja pino, voi kulkea yhdellä tavalla. Puun läpi kulkemiseen on useita tapoja, jotka on lueteltu seuraavasti:
- Ennakkotilaa läpikulku
- Tilauksen läpikulku
- Postimääräyksen läpikulku
Joten tässä artikkelissa käsittelemme yllä lueteltuja puun poikkimisen tekniikoita. Aloitetaan nyt keskustelemaan puiden läpikulkutavoista.
Ennakkotilaa läpikulku
Tämä tekniikka noudattaa 'juuri vasen oikea' -käytäntöä. Se tarkoittaa, että ensin käydään juurisolmussa, jonka jälkeen vasemmanpuoleinen alipuu kuljetaan rekursiivisesti ja lopuksi oikea alipuu rekursiivisesti. Koska juurisolmu kulkee ennen (tai ennen) vasenta ja oikeaa alipuuta, sitä kutsutaan preorder traversaliksi.
Joten ennakkotilauksen läpikäymisessä jokaisessa solmussa käydään ennen molempia sen alipuita.
Ennakkotilauksen läpikäymisen sovelluksia ovat -
- Sitä käytetään puun kopion luomiseen.
- Sitä voidaan käyttää myös lausekepuun etuliitelausekkeen saamiseksi.
Algoritmi
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Esimerkki
Katsotaanpa nyt esimerkkiä ennakkotilauksen läpikulkutekniikasta.
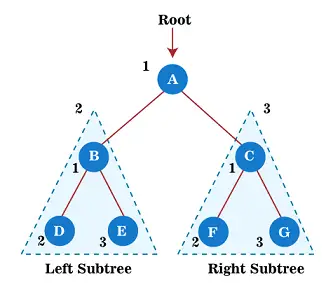
Aloita nyt ennakkotilauksen läpikulku yllä olevassa puussa. Ensin kuljemme juurisolmun läpi A; sen jälkeen siirry sen vasempaan alipuuhun B , joka myös kuljetetaan ennakkotilauksena.
Joten vasemmalle alipuulle B ensin juurisolmu B kulkee itsensä läpi; sen jälkeen sen vasen alipuu D ajetaan läpi. Solmusta lähtien D hänellä ei ole lapsia, siirry oikeaan alipuuhun JA . Koska solmulla E ei myöskään ole lapsia, juurisolmun A vasemman alipuun läpikulku on valmis.
median siirto
Siirry nyt kohti juurisolmun A oikeaa alipuuta, joka on C. Joten oikealle alipuulle C ensin juurisolmu C on kulkenut itsensä läpi; sen jälkeen sen vasen alipuu F ajetaan läpi. Solmusta lähtien F hänellä ei ole lapsia, siirry oikeaan alipuuhun G . Koska solmulla G ei myöskään ole lapsia, juurisolmun A oikean alipuun läpikulku on valmis.
merkkijono int-muunnin
Siksi kaikki puun solmut ajetaan läpi. Joten yllä olevan puun ennakkotilauksen läpikäynnin tulos on -
A → B → D → E → C → F → G
Saat lisätietoja ennakkotilauksen läpikäymisestä tietorakenteessa seuraamalla linkkiä Ennakkotilaa läpikulku .
Postimääräyksen läpikulku
Tämä tekniikka noudattaa 'vasen-oikea juuri' -käytäntöä. Se tarkoittaa, että juurisolmun ensimmäinen vasen alipuu ajetaan, sen jälkeen rekursiivisesti oikean alipuun läpi ja lopuksi juurisolmun läpi. Koska juurisolmu kulkee vasemman ja oikean alipuun jälkeen (tai sen jälkeen), sitä kutsutaan postorder traversaliksi.
Joten postorder-läpikulussa jokaisessa solmussa käydään molempien alipuidensa jälkeen.
Postorder traversal -sovellukset sisältävät -
- Sitä käytetään puun poistamiseen.
- Sitä voidaan käyttää myös lausekepuun postfix-lausekkeen saamiseksi.
Algoritmi
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Esimerkki
Katsotaanpa nyt esimerkkiä postorder traversal -tekniikasta.

Aloita nyt postorder-läpiviennin soveltaminen yllä olevaan puuhun. Ensin kuljemme vasemman alipuun B läpi, joka ajetaan jälkijärjestyksessä. Sen jälkeen kuljemme oikean alipuun läpi C postorderissa. Ja lopuksi yllä olevan puun juurisolmu, eli A , ajetaan.
Joten vasemmalle alipuulle B ensin sen vasen alipuu D ajetaan läpi. Solmusta lähtien D hänellä ei ole lapsia, poikki oikea alipuu JA . Koska solmulla E ei myöskään ole lapsia, siirry juurisolmuun B. Solmun läpikäynnin jälkeen B, juurisolmun A vasemman alipuun läpikulku on valmis.
Siirry nyt kohti juurisolmun A oikeaa alipuuta, joka on C. Joten oikealle alipuulle C ensin sen vasen alipuu F ajetaan läpi. Solmusta lähtien F hänellä ei ole lapsia, poikki oikea alipuu G . Koska solmulla G ei myöskään ole lapsia, niin lopulta oikean alipuun juurisolmu, ts. C, ajetaan läpi. Juurisolmun A oikean alipuun läpikulku on valmis.
Viimeinkin ylitä tietyn puun juurisolmu, eli A . Juurisolmun läpikäynnin jälkeen annetun puun postorder-läpikulku on valmis.
Siksi kaikki puun solmut ajetaan läpi. Joten, yllä olevan puun postorder-läpikulun tulos on -
D → E → B → F → G → C → A
verkkotopologiat
Saat lisätietoja postorder-läpikulusta tietorakenteessa napsauttamalla linkkiä Postimääräyksen läpikulku .
Tilauksen läpikulku
Tämä tekniikka noudattaa 'vasen juuri oikea' -käytäntöä. Se tarkoittaa, että ensimmäisessä vasemmassa alipuussa käydään sen jälkeen, kun juurisolmu on kuljetettu, ja lopuksi alipuun oikeanpuoleinen alipuu. Koska juurisolmu kulkee vasemman ja oikean alipuun välillä, sitä kutsutaan inorder traversaliksi.
Joten järjestyksen läpikäymisessä jokaisessa solmussa käydään sen alipuiden välissä.
Inorder traversal -sovellukset sisältävät -
- Sitä käytetään saamaan BST-solmut kasvavassa järjestyksessä.
- Sitä voidaan käyttää myös lausekepuun etuliitelausekkeen saamiseksi.
Algoritmi
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Esimerkki
Katsotaanpa nyt esimerkkiä Inorder-läpikulkutekniikasta.

Aloita nyt inorder traversalin soveltaminen yllä olevaan puuhun. Ensin kuljemme vasemman alipuun poikki B jotka ajetaan järjestyksessä. Sen jälkeen kuljemme juurisolmun läpi A . Ja lopuksi oikea alipuu C ajetaan järjestyksessä.
Joten vasemmalle alipuulle B , ensinnäkin sen vasen alipuu D ajetaan läpi. Solmusta lähtien D sillä ei ole lapsia, joten sen läpikäynnin jälkeen solmu B ajetaan, ja lopulta solmun B oikea alipuu, eli JA , ajetaan. Solmulla E ei myöskään ole lapsia; siksi juurisolmun A vasemman alipuun läpikulku on valmis.
sanakirja c#
Sen jälkeen ajetaan tietyn puun juurisolmun läpi, eli A .
Lopuksi siirry kohti juurisolmun A oikeaa alipuuta, joka on C. Eli oikealle alipuulle C; ensinnäkin sen vasen alipuu F ajetaan läpi. Solmusta lähtien F hänellä ei ole lapsia, node C ajetaan ja lopulta solmun C oikea alipuu, eli G , ajetaan. Solmulla G ei myöskään ole lapsia; siksi juurisolmun A oikean alipuun läpikulku on valmis.
Kun kaikki puun solmut on ajettu läpi, tietyn puun järjestysläpikulku on valmis. Yllä olevan puun järjestyksen läpikäynnin tulos on -
D → B → E → A → F → C → G
Lisätietoa tietorakenteessa tapahtuvasta järjestyksen läpikäymisestä voit seurata linkkiä Inorder Traversal .
Puun läpikulkutekniikoiden monimutkaisuus
Edellä käsiteltyjen puun läpikulkutekniikoiden aikamonimutkaisuus on Päällä) , missä 'n' on binääripuun kokoinen.
Yllä käsiteltyjen puiden läpikulkutekniikoiden avaruusmonimutkaisuus taas on O(1) jos emme ota huomioon funktiokutsujen pinon kokoa. Muuten näiden tekniikoiden monimutkaisuus on Vai niin) , missä 'h' on puun korkeus.
Tree traversalin toteuttaminen
Katsotaanpa nyt edellä käsiteltyjen tekniikoiden toteutusta eri ohjelmointikielillä.
Ohjelmoida: Kirjoita ohjelma puun läpikulkutekniikoiden toteuttamiseksi C-kielellä.
pilvilaskentasovellukset
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Lähtö

Ohjelmoida: Kirjoita ohjelma puun läpikulkutekniikoiden toteuttamiseksi C#:ssa.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Lähtö

Ohjelmoida: Kirjoita ohjelma puun läpikulkutekniikoiden toteuttamiseksi C++:ssa.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Lähtö
Yllä olevan koodin suorittamisen jälkeen tulos on -

Johtopäätös
Tässä artikkelissa olemme keskustelleet erityyppisistä puiden läpikulkutekniikoista: ennakkotilauksen läpikulku, järjestysläpikulku ja postorder-läpikulku. Olemme nähneet nämä tekniikat yhdessä algoritmin, esimerkin, monimutkaisuuden ja toteutuksen kanssa C-, C++-, C#- ja javassa.
Eli siinä kaikki artikkelista. Toivottavasti se on hyödyllinen ja informatiivinen sinulle.
