Termi Memoisointi tulee latinan sanasta muistio ( muistaa ), joka on yleisesti lyhennetty amerikanenglanniksi muistioksi ja joka tarkoittaa funktion tulosten muuntamista muistettavaksi.
Laskennassa memoisointia käytetään nopeuttamaan tietokoneohjelmia poistamalla tulosten toistuva laskeminen ja välttämällä toistuvia kutsuja funktioille, jotka käsittelevät samaa syötettä.

Mikä on memoisointi
Sisällysluettelo
- Mikä on memoisointi?
- Miksi Memoizationia käytetään>
- Missä Memoizationia käytetään?
- Memoisoinnin tyypit
- Kuinka memoisointitekniikkaa käytetään dynaamisessa ohjelmoinnissa?
- Miten memoisointi eroaa taulukoinnista?
- Memoisoinnin koodauskäytännöt
- UKK
- 1) Onko memoisointi parempi kuin DP?
- 2) Onko memoisointi sama asia kuin välimuisti?
- 3) Miksi muistiinpano tapahtuu ylhäältä alas?
- 4) Käyttääkö memoisointi rekursiota?
- 5) Pitäisikö minun käyttää taulukointia vai muistiinpanoa?
- 6) Missä memoisointia käytetään?
- 7) Miksi sitä kutsutaan muistelemiseksi?
- 8) Miten muistiin kirjoittaminen vähentää ajan monimutkaisuutta?
- 9) Mitä eroa on muistiinpanon ja välimuistin välillä?
- 10) Miksi taulukointi on nopeampaa kuin muistiin kirjoittaminen?
- Johtopäätös
Miksi Memoizationia käytetään?
Memoisointi on erityinen muoto välimuisti jota käytetään dynaaminen ohjelmointi . Välimuistin tarkoituksena on parantaa ohjelmiemme suorituskykyä ja pitää tiedot saatavilla, jotta niitä voidaan käyttää myöhemmin. Pohjimmiltaan se tallentaa aliongelman aiemmin lasketun tuloksen ja käyttää tallennettua tulosta samalle osatehtävälle. Tämä poistaa ylimääräisen vaivan laskea uudestaan ja uudestaan samasta ongelmasta. Ja tiedämme jo, että jos sama ongelma toistuu uudestaan ja uudestaan, se ongelma on luonteeltaan rekursiivinen.
Missä Memoizationia käytetään?
Voimme käyttää memoisointitekniikkaa, kun aiemmin laskettujen tulosten käyttö tulee kuvaan. Tällaista ongelmaa käytetään enimmäkseen kontekstissa rekursio , varsinkin niihin liittyvien ongelmien kanssa päällekkäisiä aliongelmia .
Otetaan esimerkki, jossa sama osaongelma toistuu uudestaan ja uudestaan.
Esimerkki, jossa näytetään muistiinpanon käyttö:
Let us try to find the factorial of a number .>
Alla on a rekursiivinen menetelmä luvun faktoriaalin löytämiseksi:
int factorial(signed int n)
{
jos (n == 0)
paluu 1;
return n * factorial(n – 1);
}
Mitä tapahtuu, jos käytämme tätä rekursiivista menetelmää?
Jos kirjoitat yllä olevan katkelman täydellisen koodin, huomaat, että koodissa on kaksi tapaa:
1. factorial(n) 2. main()>
Jos meillä on useita kyselyitä faktoriaalin löytämiseksi, kuten 2, 3, 9 ja 5:n faktoriaalin löytäminen, meidän on kutsuttava factorial()-menetelmää 4 kertaa:
factorial(2) factorial(3) factorial(9) factorial(5)>
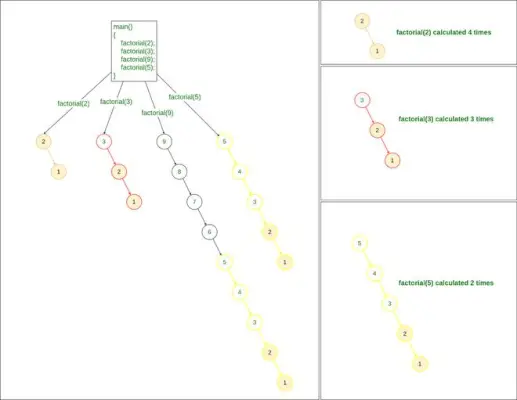
Rekursiivinen menetelmä Faktoriaalin löytämiseksi
Joten on turvallista sanoa, että K-lukujen tekijöiden löytämiseen tarvitaan aikamonimutkaisuus O(N*K)
- PÄÄLLÄ) löytääksesi tietyn luvun kertoimen ja
- NUOLI) kutsua factorial()-metodia K eri aikoina.
Kuinka memoisointi voi auttaa tällaisissa ongelmissa?
Jos huomaamme yllä olevassa ongelmassa, kun lasketaan kertoimella 9:
lateksimatriisi
- Laskemme 2:n faktoriaalin
- Laskemme myös tekijän 3,
- ja Laskemme myös 5:n faktoriaalin
Siksi, jos tallennamme jokaisen yksittäisen kertoimen tuloksen ensimmäisellä laskentakerralla, voimme helposti palauttaa minkä tahansa vaaditun luvun tekijän vain O(1) ajassa. Tämä prosessi tunnetaan nimellä Memoisointi .
Ratkaisu Memoization-toiminnolla (Kuinka memoisointi toimii?):
Jos löydämme ensin 9:n kertoimen ja tallennamme yksittäisten osaongelmien tulokset, voimme helposti tulostaa kunkin syötteen kertoimen O(1:ssä).
Siksi tekijälukujen löytäminen muistiin tallentamista käyttämällä on aika monimutkaisuus PÄÄLLÄ)
- PÄÄLLÄ) löytääksesi suurimman syötteen faktoriaalin
- O(1) tulostaaksesi kunkin syötteen kertoimen.
Memoisoinnin tyypit
Memoisoinnin toteutus riippuu muuttuvista parametreista, jotka ovat vastuussa ongelman ratkaisemisesta. Muistiinpanotekniikassa käytetään useita välimuistin ulottuvuuksia. Alla on joitain niistä:
- 1D Muistiinpano: Rekursiivinen funktio, jolla on vain yksi argumentti, jonka arvo ei ollut vakio jokaisen funktiokutsun jälkeen.
- 2D Muistiinpano: Rekursiivinen funktio, jolla on vain kaksi argumenttia, joiden arvo ei ollut vakio jokaisen funktiokutsun jälkeen.
- 3D Memoisointi : Rekursiivinen funktio, jolla on vain kolme argumenttia, joiden arvot eivät olleet vakioita jokaisen funktiokutsun jälkeen.
Kuinka memoisointitekniikkaa käytetään dynaamisessa ohjelmoinnissa?
Dynaaminen ohjelmointi auttaa ratkaisemaan tehokkaasti ongelmia, joissa on päällekkäisiä aliongelmia ja optimaaliset alirakenteen ominaisuudet. Dynaamisen ohjelmoinnin ideana on jakaa ongelma pienempiin osaongelmiin ja tallentaa tulos tulevaa käyttöä varten, jolloin lopputulosta ei tarvitse laskea toistuvasti.
Dynaamisen ohjelmointiratkaisun muotoiluun on kaksi tapaa:
- Ylhäältä alas -lähestymistapa: Tämä lähestymistapa noudattaa muisteleminen tekniikka . Se koostuu rekursio ja välimuisti . Laskennassa rekursio edustaa prosessia, jossa funktioita kutsutaan toistuvasti, kun taas välimuisti viittaa välitulosten tallennusprosessiin.
- Alhaalta ylös -lähestymistapa: Tämä lähestymistapa käyttää taulukointi tekniikka dynaamisen ohjelmointiratkaisun toteuttamiseen. Se ratkaisee samat ongelmat kuin ennenkin, mutta ilman rekursiota. Tässä lähestymistavassa iteraatio korvaa rekursion. Näin ollen ei ole pinon ylivuotovirhettä tai rekursiivisten proseduurien ylikuormitusta.
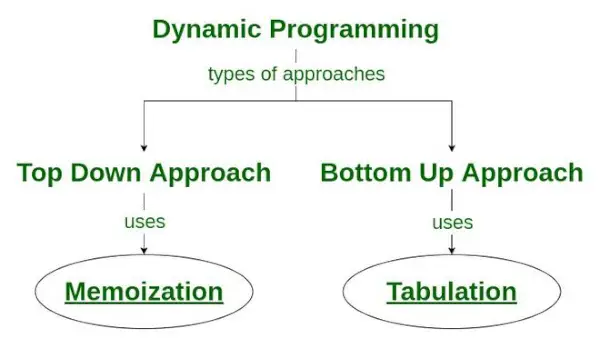
Kuinka memoisointitekniikkaa käytetään dynaamisessa ohjelmoinnissa
Miten memoisointi eroaa taulukoinnista?

Taulukko vs muistiinpano
Katso lisätietoja: Taulukko vs. muistiinpano
Memoisoinnin koodauskäytännön ongelmat
| Kysymys | Artikla | Harjoitella | Video |
|---|---|---|---|
| Laske tapoja päästä n-portaalle | Näytä | Ratkaista | Katsella |
| Word Break ongelma | DP-32 | Näytä | Ratkaista | Katsella |
| Ohjelma Fibonacci-numeroille | Näytä | Ratkaista | Katsella |
| n. katalaaninumero | Näytä | Ratkaista | Katsella |
| Kultakaivoksen ongelma | Näytä | Ratkaista | Katsella |
| Osajoukon summa -ongelma | Näytä | Ratkaista | Katsella |
| Tangon leikkaaminen | Näytä | Ratkaista | Katsella |
| Pienin kustannuspolku | Näytä | Ratkaista | Katsella |
| Vähimmäismäärä hyppyjä päästäksesi päähän | Näytä | Ratkaista | Katsella |
| Pisin palindrominen osamerkkijono | Sarja 1 | Näytä | Ratkaista | Katsella |
| Pisin toistuva jakso | Näytä | Ratkaista | Katsella |
| Laske tavat päästä n:nnelle portaalle vaiheiden 1, 2 tai 3 avulla | Näytä | Ratkaista | Katsella |
| Laske erilaisia tapoja ilmaista N lukujen 1, 3 ja 4 summana | Näytä | Ratkaista | Katsella |
| Laske kuinka monta tapaa kattaa matka | Näytä | Ratkaista | Katsella |
| Niiden taulukoiden määrä, joissa on peräkkäinen elementti eri arvoilla | Näytä | Ratkaista | Katsella |
| Suurin Summa vierekkäinen Subarray | Näytä | Ratkaista | Katsella |
| Pienin summa vierekkäinen aliryhmä | Näytä | Ratkaista | Katsella |
| Ainutlaatuisia polkuja esteitä sisältävässä ruudukossa | Näytä | Ratkaista | Katsella |
| Eri tapoja summata n käyttämällä lukuja, jotka ovat suurempia tai yhtä suuria kuin m | Näytä | Ratkaista | Katsella |
Usein kysytyt kysymykset (FAQ) Memoizationista
1: Onko memoisointi parempi kuin DP?
Memoisointi on ylhäältä alaspäin suuntautuva lähestymistapa ongelman ratkaisemiseen dynaamisen ohjelmoinnin avulla. Sitä kutsutaan muistiinpanemiseksi, koska luomme muistion kunkin ongelman ratkaisemisesta palautetuista arvoista.
2: Onko memoisointi sama asia kuin välimuisti?
Memoisointi on itse asiassa erityinen välimuistin tyyppi. Termi välimuisti voi yleensä viitata mihin tahansa tallennustekniikkaan (kuten HTTP-välimuistiin) tulevaa käyttöä varten, mutta muistiin merkitseminen viittaa tarkemmin välimuistitoimintoon, joka palauttaa arvon.
3: Miksi muistiinpano tapahtuu ylhäältä alas?
Ylhäältä alas -lähestymistapa jakaa suuren ongelman useisiin osaongelmiin. Jos osaongelma on jo ratkaistu, käytä vastausta uudelleen. Muussa tapauksessa Ratkaise aliongelma ja tallenna tulos johonkin muistiin.
4: Käyttääkö memoisointi rekursiota?
Memoisointi noudattaa ylhäältä alas -lähestymistapaa ongelman ratkaisemiseksi. Se koostuu rekursiosta ja välimuistista. Laskennassa rekursio edustaa prosessia, jossa funktioita kutsutaan toistuvasti, kun taas välimuisti viittaa välitulosten tallennusprosessiin.
5: Pitäisikö minun käyttää taulukointia vai muistiinpanoa?
Ongelmissa, jotka edellyttävät kaikkien aliongelmien ratkaisemista, taulukointi tyypillisesti ylittää muistiinpanon vakiokertoimella. Tämä johtuu siitä, että taulukossa ei ole ylimääräistä rekursiota, mikä vähentää aikaa, joka kuluu rekursiokutsupinon selvittämiseen pinomuistista.
Aina kun aliongelma on ratkaistava alkuperäisen ongelman ratkaisemiseksi, muistiin tallentaminen on parempi, koska osaongelma ratkaistaan laiskasti, eli suoritetaan vain tarvittavat laskelmat.
6: Missä memoisointia käytetään?
Memoisointi on optimointitekniikka, jota käytetään tietokoneohjelmien nopeuttamiseen tallentamalla kalliiden toimintokutsujen tulokset välimuistiin ja palauttamalla ne, kun samat syötteet kohdataan uudelleen.
7: Miksi sitä kutsutaan muistelemiseksi?
Termi memoisointi tulee latinalaisesta sanasta memorandum (muistamaan), joka on yleisesti lyhennetty amerikanenglanniksi memoksi ja joka tarkoittaa funktion tulosten muuntamista muistettavaksi.
8: Kuinka muistiinpano vähentää ajan monimutkaisuutta?
Saman ongelman ratkaiseminen yhä uudelleen vie aikaa ja lisää koko ohjelman ajonaikaista monimutkaisuutta. Tämä ongelma voidaan ratkaista ylläpitämällä välimuistia tai muistia, johon tallennamme jo lasketun ongelman tuloksen jollekin tietylle syötteelle. Joten jos emme halua laskea samaa ongelmaa uudelleen, voimme yksinkertaisesti käyttää muistiin tallennettua tulosta ja vähentää ajan monimutkaisuutta.
9: Mitä eroa on muistiinpanon ja välimuistin välillä?
Muistiinpano on itse asiassa tietyntyyppinen välimuisti, jossa funktion palautusarvo tallennetaan välimuistiin syötteen perusteella. Välimuisti on yleisempi termi. Esimerkiksi HTTP-välimuisti on välimuisti, mutta se ei ole memoisointia.
10: Miksi taulukointi on nopeampaa kuin muistiin kirjoittaminen?
Taulukointi on yleensä nopeampaa kuin memoisointi, koska se on iteratiivista ja aliongelmien ratkaiseminen ei vaadi rekursiivisia kutsuja.
Memoisointi on tietojenkäsittelytieteessä käytetty tekniikka, joka nopeuttaa rekursiivisten tai laskennallisesti kalliiden funktioiden suorittamista tallentamalla välimuistiin funktiokutsujen tulokset ja palauttamalla välimuistiin tallennetut tulokset, kun samat syötteet toistuvat.
Memoisoinnin perusideana on tallentaa funktion tulos tietylle syötejoukolle ja palauttaa välimuistissa oleva tulos, jos funktiota kutsutaan uudelleen samoilla tuloilla. Tämä tekniikka voi säästää laskenta-aikaa, erityisesti funktioissa, joita kutsutaan usein tai joiden aika monimutkaisuus on suuri.
Tässä on vaiheittainen opas muistiinpanon toteuttamiseen:
kuinka lukea csv-tiedostoa javassa
Tunnista toiminto, jonka haluat optimoida muistojen avulla. Tällä funktiolla pitäisi olla toistuvia ja kalliita laskutoimituksia samalle tulolle.
Luo sanakirjaobjekti tallentaaksesi funktion välimuistissa olevat tulokset. Sanakirjan avainten tulee olla funktion syöttöparametreja, ja arvojen tulee olla laskettuja tuloksia.
Tarkista funktion alussa, ovatko syöttöparametrit jo olemassa välimuistin sanakirjassa. Jos ne ovat, palauta välimuistissa oleva tulos.
Jos syöttöparametrit eivät ole välimuistin sanakirjassa, laske tulos ja tallenna se välimuistin sanakirjaan syöteparametrien avaimella.
Palauta laskettu tulos.
Tässä on Python-koodiesimerkki memoisoinnin toteuttamisesta sanakirjan avulla:
Python 3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Lähtö
>
Yllä olevassa koodissa määritämme fibonacci-nimisen funktion, joka laskee Fibonacci-sekvenssin n:nnen luvun. Käytämme välimuisti-nimistä sanakirjaobjektia tallentamaan funktiokutsujen tulokset. Jos syöttöparametri n on jo olemassa välimuistin sanakirjassa, palautetaan välimuistissa oleva tulos. Muussa tapauksessa laskemme tuloksen käyttämällä rekursiivisia kutsuja fibonacci-funktiolle ja tallennamme sen välimuistin sanakirjaan ennen sen palauttamista.
Muistiinpanon avulla voidaan optimoida monien toimintojen suorituskyky, jotka vaativat toistuvia ja kalliita laskelmia. Tallentamalla funktiokutsujen tulokset välimuistiin voimme välttää turhat laskelmat ja nopeuttaa funktion suorittamista.
Johtopäätös
Memoisointi on ohjelmointikonsepti ja sitä voidaan soveltaa mihin tahansa ohjelmointikieleen. Sen ehdoton tavoite on optimoida ohjelma. Yleensä tämä ongelma havaitaan, kun ohjelmat suorittavat raskaita laskutoimituksia. Tämä tekniikka tallentaa välimuistiin kaikki edelliset lasketut tulokset, jotta sitä ei tarvitse laskea uudelleen samalle ongelmalle.
Aiheeseen liittyvät artikkelit:
- Muistiinpano koristeilla Pythonissa
- JavaScript-muistiinpano
