Pino on lineaarinen tietorakenne, joka seuraa LIFO (Last-In-First-Out) periaate. Pinolla on yksi pää, kun taas jonolla on kaksi päätä ( edessä ja takana ). Se sisältää vain yhden osoittimen yläosoitin osoittaa pinon ylimpään elementtiin. Aina kun elementti lisätään pinoon, se lisätään pinon yläosaan ja elementti voidaan poistaa vain pinosta. Toisin sanoen a pino voidaan määritellä säiliöksi, johon lisääminen ja poistaminen voidaan tehdä pinon yläpäänä tunnetusta päästä.

Jotkut pinoon liittyvät avainkohdat

• Sitä kutsutaan pinoksi, koska se käyttäytyy kuin todellinen pino, kirjapinot jne.
• Pino on abstrakti tietotyyppi, jolla on ennalta määrätty kapasiteetti, mikä tarkoittaa, että se voi tallentaa rajoitetun kokoisia elementtejä.
• Se on tietorakenne, joka noudattaa tiettyä järjestystä elementtien lisäämiseksi ja poistamiseksi, ja tämä järjestys voi olla LIFO tai FILO.

Stackin työskentely

Pino toimii LIFO-kuviolla. Kuten alla olevasta kuvasta voidaan havaita, pinossa on viisi muistilohkoa; siksi pinon koko on 5.

linuxin pikakuvakkeet

Oletetaan, että haluamme tallentaa elementit pinoon ja oletetaan, että pino on tyhjä. Olemme ottaneet koon 5 pinon alla olevan kuvan mukaisesti, jossa työnnämme elementtejä yksitellen, kunnes pino täyttyy.

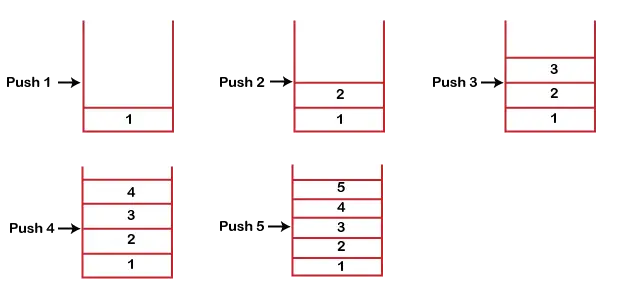
Koska pinomme on täynnä, koska pinon koko on 5. Yllä olevissa tapauksissa voimme havaita, että se menee ylhäältä alas, kun olimme syöttämässä pinon uutta elementtiä. Pino täytetään alhaalta ylöspäin.

Kun suoritamme pinon poistotoiminnon, on vain yksi tapa päästä sisään ja poistua, koska toinen pää on suljettu. Se noudattaa LIFO-mallia, mikä tarkoittaa, että ensin syötetty arvo poistetaan viimeisenä. Yllä olevassa tapauksessa arvo 5 syötetään ensin, joten se poistetaan vasta, kun kaikki muut elementit on poistettu.

Tavalliset pinotoiminnot

Seuraavassa on joitain yleisiä pinossa toteutettuja toimintoja:

alennuskuva

työntää():Kun lisäämme elementin pinoon, toiminto tunnetaan työntönä. Jos pino on täynnä, ylivuototila ilmenee.pop():Kun poistamme elementin pinosta, toiminto tunnetaan popina. Jos pino on tyhjä, se tarkoittaa, että pinossa ei ole elementtiä, tätä tilaa kutsutaan alivuototilaksi.on tyhjä():Se määrittää, onko pino tyhjä vai ei.on täynnä():Se määrittää, onko pino täynnä vai ei.kurkistaa():Se palauttaa elementin annettuun kohtaan.Kreivi():Se palauttaa pinossa käytettävissä olevien elementtien kokonaismäärän.muuttaa():Se muuttaa elementin annetussa paikassa.näyttö():Se tulostaa kaikki pinossa olevat elementit.

PUSH-toiminto

PUSH-toimintoon liittyvät vaiheet on annettu alla:

• Ennen kuin lisäät elementin pinoon, tarkistamme, onko pino täynnä.
• Jos yritämme lisätä elementin pinoon ja pino on täynnä, ylivuoto tila tapahtuu.
• Kun alustamme pinon, asetamme topin arvoksi -1 varmistaaksemme, että pino on tyhjä.
• Kun uusi elementti työnnetään pinoon, ensin alkuun arvo kasvaa, ts. top=top+1, ja elementti sijoitetaan uuteen paikkaan alkuun .
• Elementit lisätään, kunnes saavutamme max pinon kokoa.

POP-toiminta

POP-toiminnon vaiheet on esitetty alla:

• Ennen kuin poistat elementin pinosta, tarkistamme onko pino tyhjä.
• Jos yritämme poistaa elementin tyhjästä pinosta, niin alivuoto tila tapahtuu.
• Jos pino ei ole tyhjä, käytämme ensin elementtiä, jota osoittaa alkuun
• Kun pop-toiminto on suoritettu, yläosaa pienennetään yhdellä, eli top=top-1 .

Stackin sovellukset

Seuraavat ovat pinon sovellukset:

Symbolien tasapainotus:Pinoa käytetään symbolin tasapainottamiseen. Meillä on esimerkiksi seuraava ohjelma:

 int main() { cout&lt;<'hello'; cout<<'javatpoint'; } < pre> <p>As we know, each program has <em>an opening</em> and <em>closing</em> braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.</p> <ul> <tr><td>String reversal:</td> Stack is also used for reversing a string. For example, we want to reverse a &apos; <strong>javaTpoint</strong> &apos; string, so we can achieve this with the help of a stack. <br> First, we push all the characters of the string in a stack until we reach the null character. <br> After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack. </tr><tr><td>UNDO/REDO:</td> It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write &apos;a&apos;, then &apos;b&apos;, and then &apos;c&apos;; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state. <br> If we want to perform UNDO operation, and want to achieve &apos;ab&apos; state, then we implement pop operation. </tr><tr><td>Recursion:</td> The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained. </tr><tr><td>DFS(Depth First Search):</td> This search is implemented on a Graph, and Graph uses the stack data structure. </tr><tr><td>Backtracking:</td> Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure. </tr><tr><td>Expression conversion:</td> Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below: <pre>Infix to prefix Infix to postfix Prefix to infix Prefix to postfix Postfix to infix</pre> </tr><tr><td>Memory management:</td> The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function call stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completed its execution, all the variables assigned in the stack are released. </tr></ul> <hr></'hello';>