Binääripuu on tasapainotettu, jos puun korkeus on O(Log n), jossa n on solmujen lukumäärä. Esimerkiksi AVL-puu säilyttää O(Log n) -korkeuden varmistamalla, että vasemman ja oikean alipuun korkeuksien ero on enintään 1. Punamustat puut säilyttävät O(Log n) -korkeuden varmistamalla, että numero mustien solmujen määrä jokaisella juuresta lehtiin -polulla on sama ja että vierekkäisiä punaisia solmuja ei ole. Balanced Binary Search -puut ovat suorituskyvyltään hyviä, koska ne tarjoavat O(log n) -aikaa etsimiseen, lisäämiseen ja poistamiseen.
Tasapainotettu binääripuu on binääripuu, joka noudattaa kolmea ehtoa:
- Vasemman ja oikean puun korkeus minkään solmun kohdalla ei eroa enempää kuin 1.
- Myös kyseisen solmun vasen alipuu on tasapainotettu.
- Myös kyseisen solmun oikea alipuu on tasapainotettu.
Yksi solmu on aina tasapainotettu. Sitä kutsutaan myös korkeudeltaan tasapainoiseksi binääripuuksi.
Esimerkki :
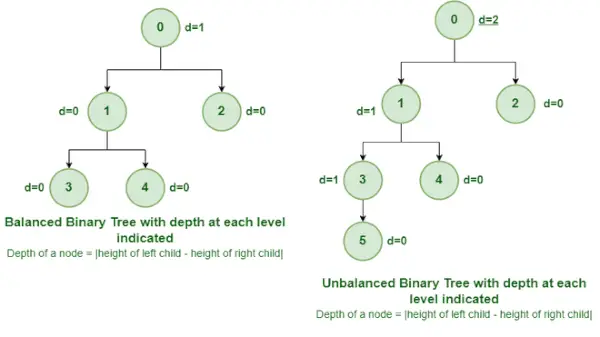
Tasapainoinen ja epätasapainoinen binaaripuu
Se on eräänlainen binääripuu, jossa kunkin solmun vasemman ja oikean alipuun korkeusero on joko 0 tai 1. Yllä olevassa kuvassa juurisolmu, jonka arvo on 0, on epätasapainossa 2 yksikön syvyydellä. .
Tasapainotetun binaaripuun sovellus:
- AVL puut
- Punainen musta puu
- Balanced Binary Search Tree
Tasapainoisen binaaripuun edut:
- Ei-tuhoisia päivityksiä tukee Balanced Binary Tree, jolla on sama asymptoottinen tehokkuus.
- Tasapainotettu binääripuu tekee mahdolliseksi aluekyselyt ja iterointi oikeassa järjestyksessä.
