Reaalimaailmassa jokaisella datalla, jonka parissa työskentelemme, ei ole tavoitemuuttujaa. Tällaista dataa ei voida analysoida valvotuilla oppimisalgoritmeilla. Tarvitsemme valvomattomien algoritmien apua. Yksi suosituimmista ohjaamattoman oppimisen analyysityypeistä on asiakkaiden segmentointi kohdistetuissa mainoksissa tai lääketieteellisessä kuvantamisessa tuntemattomien tai uusien tartuntaalueiden ja monien muiden käyttötapausten löytämiseksi, joista keskustelemme tarkemmin tässä artikkelissa.
Sisällysluettelo
- Mitä on klusterointi?
- Klusterin tyypit
- Klusterin käyttötarkoitukset
- Klusterointialgoritmien tyypit
- Klusterin sovellukset eri aloilla:
- Usein kysytyt kysymykset (FAQ) klusteroinnista
Mitä on klusterointi?
Tietopisteiden ryhmittelyä niiden samankaltaisuuden perusteella kutsutaan klusteriksi tai klusterianalyysiksi. Tämä menetelmä on määritelty haarassa Ohjaamaton oppiminen , jonka tarkoituksena on saada oivalluksia merkitsemättömistä tietopisteistä, toisin sanoen ohjattua oppimista meillä ei ole tavoitemuuttujaa.
Klusteroinnilla pyritään muodostamaan heterogeenisestä tietojoukosta homogeenisten tietopisteiden ryhmiä. Se arvioi samankaltaisuuden esimerkiksi euklidisen etäisyyden, kosinin samankaltaisuuden, Manhattanin etäisyyden jne. perusteella ja ryhmittele sitten pisteet, joilla on korkein samankaltaisuuspisteet.
Esimerkiksi alla annetussa kaaviossa näemme selvästi, että etäisyyden perusteella muodostuu 3 pyöreää klusteria.
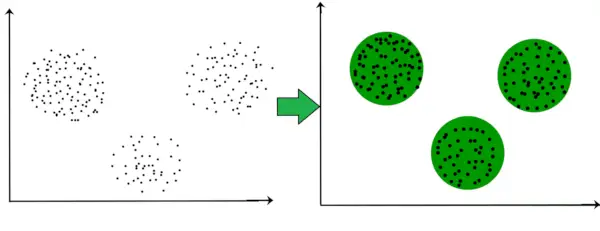
Nyt ei ole välttämätöntä, että muodostuneiden klustereiden on oltava pyöreitä. Klusterien muoto voi olla mielivaltainen. On monia algoritmeja, jotka toimivat hyvin mielivaltaisen muotoisten klustereiden havaitsemisessa.
Järjestä satunnaisella sql:llä
Esimerkiksi alla olevassa kaaviossa näemme, että muodostuneet klusterit eivät ole muodoltaan pyöreitä.

Klusterin tyypit
Yleisesti ottaen on olemassa kahdenlaisia klusterointityyppejä, jotka voidaan suorittaa samanlaisten datapisteiden ryhmittelyyn:
- Kova klusterointi: Tämän tyyppisessä klusteroinnissa jokainen datapiste kuuluu klusteriin kokonaan tai ei. Oletetaan esimerkiksi, että datapisteitä on 4 ja meidän on ryhmitettävä ne 2 klusteriin. Joten jokainen datapiste kuuluu joko klusteriin 1 tai klusteriin 2.
| Datapisteet | Klusterit |
|---|---|
| A | C1 |
| B | C2 |
| C | C2 |
| D | C1 |
- Pehmeä klusteri: Tämän tyyppisessä klusteroinnissa kunkin datapisteen osoittamisen sijaan erilliseen klusteriin arvioidaan sen pisteen todennäköisyys tai todennäköisyys, että klusteri on kyseessä. Oletetaan esimerkiksi, että datapisteitä on 4 ja meidän on ryhmitettävä ne 2 klusteriin. Joten arvioimme todennäköisyyttä, että datapiste kuuluu molempiin klustereihin. Tämä todennäköisyys lasketaan kaikille datapisteille.
| Datapisteet | Todennäköisyys C1 | Todennäköisyys C2 |
| A | 0,91 | 0.09 |
| B | 0.3 | 0.7 |
| C | 0.17 | 0,83 |
| D | 1 | 0 |
Klusterin käyttötarkoitukset
Ennen kuin aloitamme klusterointialgoritmien tyypeillä, käymme läpi klusterointialgoritmien käyttötapaukset. Klusterointialgoritmeja käytetään pääasiassa:
- Markkinoiden segmentointi – Yritykset käyttävät klusterointia asiakkaidensa ryhmittelyyn ja kohdistettujen mainosten avulla houkutellakseen lisää yleisöä.
- Sosiaalisen verkoston analyysi – Sosiaalisen median sivustot käyttävät tietojasi ymmärtääkseen selauskäyttäytymistäsi ja tarjotakseen sinulle kohdennettuja ystäväsuosituksia tai sisältösuosituksia.
- Lääketieteellinen kuvantaminen – Lääkärit käyttävät klusterointia selvittääkseen sairaita alueita diagnostisista kuvista, kuten röntgenkuvista.
- Anomalian havaitseminen – Voimme käyttää klusterointia tunnistaaksemme poikkeamat reaaliaikaisen tietojoukon virrasta tai ennustaaksemme vilpillisiä tapahtumia.
- Yksinkertaista suurten tietojoukkojen käsittelyä – Jokaiselle klusterille annetaan klusterin tunnus, kun klusterointi on valmis. Nyt voit pienentää ominaisuusjoukon koko ominaisuusjoukon sen klusteritunnukseksi. Klusterointi on tehokasta, kun se voi edustaa monimutkaista tapausta suoraviivaisella klusteritunnuksella. Samaa periaatetta käyttämällä tietojen klusterointi voi tehdä monimutkaisista tietojoukoista yksinkertaisempia.
Klusteroinnissa on monia muita käyttötapauksia, mutta klusteroinnissa on joitain tärkeimpiä ja yleisimpiä käyttötapauksia. Jatkossa keskustelemme klusterointialgoritmeista, jotka auttavat sinua suorittamaan yllä olevat tehtävät.
rakentajat javassa
Klusterointialgoritmien tyypit
Pintatasolla klusterointi auttaa strukturoimattoman datan analysoinnissa. Graafinen piirtäminen, lyhin etäisyys ja datapisteiden tiheys ovat muutamia elementtejä, jotka vaikuttavat klusterin muodostumiseen. Klusterointi on prosessi, jossa määritetään, kuinka sukua objektit ovat samankaltaisuusmitan metriikassa. Samankaltaisuusmittarit on helpompi paikantaa pienemmissä ominaisuuksissa. Samankaltaisuusmittausten luominen muuttuu vaikeammaksi ominaisuuksien määrän kasvaessa. Tietojen louhinnassa käytettävän klusterointialgoritmin tyypistä riippuen käytetään useita tekniikoita datan ryhmittelyyn tietojoukoista. Tässä osassa kuvataan klusterointitekniikat. Erilaisia klusterointialgoritmeja ovat:
- Centroid-pohjainen klusteri (osiointimenetelmät)
- Tiheyspohjainen klusterointi (mallipohjaiset menetelmät)
- Yhteyksiin perustuva klusterointi (hierarkkinen klusterointi)
- Jakelupohjainen klusterointi
Käymme läpi kaikki nämä tyypit lyhyesti.
1. Osiointimenetelmät ovat helpoimpia klusterointialgoritmeja. He ryhmittelevät datapisteitä läheisyyden perusteella. Yleensä näille algoritmeille valitut samankaltaisuusmitat ovat Euklidinen etäisyys, Manhattan Distance tai Minkowski Distance. Tietojoukot erotetaan ennalta määrättyyn määrään klustereita, ja jokaiseen klusteriin viitataan arvovektorilla. Verrattuna vektoriarvoon, syöttödatamuuttuja ei näytä eroa ja liittyy klusteriin.
Näiden algoritmien ensisijainen haittapuoli on vaatimus, että määritämme klustereiden lukumäärän k joko intuitiivisesti tai tieteellisesti (käyttäen kyynärpäämenetelmää) ennen kuin mikään klusteroiva koneoppimisjärjestelmä alkaa allokoida datapisteitä. Tästä huolimatta se on edelleen suosituin klusterointityyppi. K- tarkoittaa ja K-medoidit klusterointi ovat esimerkkejä tämäntyyppisestä klusteroinnista.
2. Tiheyspohjainen klusterointi (mallipohjaiset menetelmät)
Tiheyspohjainen klusterointi, mallipohjainen menetelmä, etsii ryhmiä datapisteiden tiheyden perusteella. Toisin kuin sentroidipohjainen klusterointi, joka edellyttää, että klusterien lukumäärä on ennalta määritetty ja on herkkä alustamiselle, tiheyteen perustuva klusterointi määrittää klusterien lukumäärän automaattisesti ja on vähemmän herkkä aloituspaikoille. Ne käsittelevät erinomaisia erikokoisia ja -muotoisia klustereita, joten ne sopivat ihanteellisesti tietojoukoille, joissa on epäsäännöllisen muotoisia tai päällekkäisiä klustereita. Nämä menetelmät hallitsevat sekä tiheitä että harvalukuisia data-alueita keskittymällä paikalliseen tiheyteen ja voivat erottaa klustereita, joilla on erilaisia morfologioita.
Sen sijaan sentroidipohjaisella ryhmittelyllä, kuten k-keskiarvolla, on vaikeuksia löytää mielivaltaisen muotoisia klustereita. Johtuen sen esiasetettu määrä klusterivaatimuksia ja äärimmäinen herkkyys sentroidien alkusijoittelulle, tulokset voivat vaihdella. Lisäksi sentroidipohjaisten lähestymistapojen taipumus tuottaa pallomaisia tai kuperia klustereita rajoittaa niiden kykyä käsitellä monimutkaisia tai epäsäännöllisen muotoisia klustereita. Yhteenvetona voidaan todeta, että tiheyteen perustuva klusterointi voittaa sentroidipohjaisten tekniikoiden haitat valitsemalla itsenäisesti klusterin koot, kestävyyden alustusta vastaan ja onnistuneesti sieppaamalla erikokoisia ja -muotoisia klustereita. Suosituin tiheyteen perustuva klusterointialgoritmi on DBSCAN .
java slice
3. Yhteyksiin perustuva klusterointi (hierarkkinen klusterointi)
Menetelmää toisiinsa liittyvien tietopisteiden kokoamiseksi hierarkkisiksi klustereiksi kutsutaan hierarkkisiksi klusteriksi. Jokainen datapiste otetaan aluksi huomioon erillisenä klusterina, joka yhdistetään myöhemmin samankaltaisimpien klusterien kanssa yhdeksi suureksi klusteriksi, joka sisältää kaikki datapisteet.
Mieti, kuinka voit järjestää esinekokoelman sen perusteella, kuinka samankaltaisia ne ovat. Jokainen objekti alkaa omana klusterinaan puun tyvestä käytettäessä hierarkkista klusterointia, joka luo dendrogrammin, puumaisen rakenteen. Lähimmät klusteriparit yhdistetään sitten suuremmiksi klusteriksi sen jälkeen, kun algoritmi tutkii, kuinka samankaltaisia objektit ovat keskenään. Kun jokainen objekti on yhdessä klusterissa puun yläosassa, yhdistämisprosessi on valmis. Erilaisten tarkkuustasojen tutkiminen on yksi hauskimmista asioista hierarkkisessa klusteroinnissa. Jos haluat saada tietyn määrän klustereita, voit leikata sen dendrogrammi tietyllä korkeudella. Mitä enemmän samankaltaisia kaksi objektia ovat klusterin sisällä, sitä lähempänä ne ovat. Se on verrattavissa esineiden luokitteluun sukupuiden mukaan, jossa lähimmät sukulaiset ovat ryhmittyneet yhteen ja leveämmät oksat merkitsevät yleisempiä yhteyksiä. Hierarkkiseen klusterointiin on kaksi lähestymistapaa:
- Divisive Clustering : Se noudattaa ylhäältä alas -lähestymistapaa, tässä katsomme kaikki datapisteet osaksi yhtä suurta klusteria ja sitten tämä klusteri jaetaan pienempiin ryhmiin.
- Agglomeratiivinen klusterointi : Se noudattaa alhaalta ylös -lähestymistapaa, tässä katsomme kaikki datapisteet yksittäisten klustereiden osaksi ja sitten nämä klusterit yhdistetään yhteen suureksi klusteriksi, jossa on kaikki datapisteet.
4. Jakelupohjainen klusterointi
Jakaumaan perustuvaa klusterointia käyttämällä tietopisteet luodaan ja järjestetään sen mukaan, kuinka heillä on taipumus pudota samaan todennäköisyysjakaumaan (kuten Gaussin, binomiaaliin tai muuhun) datassa. Tietoelementit ryhmitellään käyttämällä todennäköisyysperusteista jakaumaa, joka perustuu tilastollisiin jakaumiin. Mukana ovat tietoobjektit, joilla on suurempi todennäköisyys olla klusterissa. Datapisteen sisällyttäminen klusteriin on epätodennäköisempää, mitä kauempana se on klusterin keskipisteestä, joka on jokaisessa klusterissa.
Tiheyteen ja rajaan perustuvien lähestymistapojen huomattava haittapuoli on tarve määrittää klusterit etukäteen joillekin algoritmeille ja ensisijaisesti klusterimuodon määrittely suurimmalle osalle algoritmeista. Vähintään yksi viritys tai hyperparametri on valittava, ja vaikka sen tekemisen pitäisi olla yksinkertaista, sen virheellisyydellä voi olla odottamattomia seurauksia. Jakelupohjaisella klusteroinnilla on selvä etu läheisyys- ja sentroidipohjaisiin klusterointimenetelmiin verrattuna joustavuuden, tarkkuuden ja klusterirakenteen suhteen. Keskeinen kysymys on, että välttääkseen ylisovitus , monet klusterointimenetelmät toimivat vain simuloidun tai valmistetun datan kanssa tai kun suurin osa datapisteistä kuuluu varmasti esiasetettuun jakaumaan. Suosituin jakelupohjainen klusterointialgoritmi on Gaussin sekoitusmalli .
Klusterin sovellukset eri aloilla:
- Markkinointi: Sitä voidaan käyttää asiakassegmenttien luonnehtimiseen ja löytämiseen markkinointitarkoituksiin.
- Biologia: Sitä voidaan käyttää luokitteluun eri kasvi- ja eläinlajien kesken.
- Kirjastot: Sitä käytetään klusteroimaan eri kirjoja aiheiden ja tietojen perusteella.
- Vakuutus: Sitä käytetään asiakkaiden, heidän toimintatapojensa ja petosten tunnistamiseen.
- Kaupunkisuunnittelu: Sen avulla tehdään taloryhmiä ja tutkitaan niiden arvoja niiden maantieteellisen sijainnin ja muiden olemassa olevien tekijöiden perusteella.
- Maanjäristystutkimukset: Oppimalla maanjäristyksen aiheuttamat alueet voimme määrittää vaaralliset vyöhykkeet.
- Kuvankäsittely : Klusteroimalla voidaan ryhmitellä samanlaisia kuvia yhteen, luokitella kuvia sisällön perusteella ja tunnistaa kuvioita kuvatiedoista.
- Genetiikka: Klusterointia käytetään ryhmittelemään geenejä, joilla on samanlaiset ilmentymismallit, ja tunnistamaan geeniverkostoja, jotka toimivat yhdessä biologisissa prosesseissa.
- Rahoittaa: Klusteroinnilla tunnistetaan markkinasegmenttejä asiakkaiden käyttäytymisen perusteella, tunnistetaan osakemarkkinatiedon malleja ja analysoidaan sijoitussalkkujen riskejä.
- Asiakaspalvelu: Klusteroinnilla ryhmitellään asiakkaiden tiedustelut ja valitukset luokkiin, tunnistetaan yleisiä ongelmia ja kehitetään kohdennettuja ratkaisuja.
- Valmistus : Klusterointia käytetään samanlaisten tuotteiden ryhmittelyyn, tuotantoprosessien optimointiin ja valmistusprosessien vikojen tunnistamiseen.
- Lääketieteellinen diagnoosi: Klusteroinnilla ryhmitellään potilaita, joilla on samankaltaisia oireita tai sairauksia, mikä auttaa tekemään tarkkoja diagnooseja ja tunnistamaan tehokkaita hoitoja.
- Petoksen havaitseminen: Klusterointia käytetään tunnistamaan epäilyttäviä malleja tai poikkeavuuksia rahoitustapahtumissa, mikä voi auttaa petosten tai muiden talousrikosten havaitsemisessa.
- Liikenneanalyysi: Klusterointia käytetään ryhmittelemään samanlaisia liikennetietoja, kuten ruuhka-aikoja, reittejä ja nopeuksia, mikä voi auttaa parantamaan liikenteen suunnittelua ja infrastruktuuria.
- Sosiaalisen verkoston analyysi: Klusterointia käytetään tunnistamaan yhteisöjä tai ryhmiä sosiaalisten verkostojen sisällä, mikä voi auttaa ymmärtämään sosiaalista käyttäytymistä, vaikuttamista ja trendejä.
- Kyberturvallisuus: Klusterointia käytetään ryhmittelemään samanlaisia verkkoliikenteen tai järjestelmän käyttäytymismalleja, mikä voi auttaa havaitsemaan ja ehkäisemään kyberhyökkäyksiä.
- Ilmastoanalyysi: Klusteroinnilla ryhmitellään samankaltaisia ilmastotietoja, kuten lämpötila, sademäärä ja tuuli, mikä voi auttaa ymmärtämään ilmastonmuutosta ja sen vaikutuksia ympäristöön.
- Urheiluanalyysi: Klusterointia käytetään pelaajien tai joukkueen suoritustietojen samankaltaisten mallien ryhmittelyyn, mikä voi auttaa analysoimaan pelaajan tai joukkueen vahvuuksia ja heikkouksia sekä tekemään strategisia päätöksiä.
- Rikosanalyysi: Klusterointia käytetään ryhmittelemään samanlaisia rikostietojen malleja, kuten sijaintia, aikaa ja tyyppiä, mikä voi auttaa tunnistamaan rikollisuuden hotspotit, ennustamaan tulevia rikollisuuksia ja parantamaan rikosten ehkäisystrategioita.
Johtopäätös
Tässä artikkelissa keskustelimme klusterista, sen tyypeistä ja sen sovelluksista todellisessa maailmassa. Ohjaamattomassa oppimisessa on paljon muutakin käsiteltävää, ja klusterianalyysi on vasta ensimmäinen askel. Tämä artikkeli voi auttaa sinua pääsemään alkuun klusterointialgoritmeilla ja auttaa sinua saamaan uuden projektin, joka voidaan lisätä portfolioosi.
Usein kysytyt kysymykset (FAQ) klusteroinnista
K. Mikä on paras klusterointimenetelmä?
10 parasta klusterointialgoritmia ovat:
- K- tarkoittaa klusterointia
- Hierarkkinen klusteri
- DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
- Gaussin sekoitusmallit (GMM)
- Agglomeratiivinen klusterointi
- Spektriklusterointi
- Mean Shift Clustering
- Affiniteettien leviäminen
- OPTIIKA (järjestyspisteet klusterointirakenteen tunnistamiseksi)
- Koivu (tasapainoinen iteratiivinen pelkistys ja klusterointi hierarkioiden avulla)
K. Mitä eroa on klusteroinnin ja luokittelun välillä?
Suurin ero klusteroinnin ja luokituksen välillä on se, että luokittelu on valvottu oppimisalgoritmi ja klusterointi on valvomaton oppimisalgoritmi. Toisin sanoen käytämme klusterointia niihin tietokokonaisuuksiin, joissa ei ole kohdemuuttujaa.
K. Mitkä ovat klusterointianalyysin edut?
Tiedot voidaan järjestää mielekkäisiin ryhmiin käyttämällä vahvaa klusterianalyysin analyyttistä työkalua. Sen avulla voit määrittää segmenttejä, löytää piilotettuja malleja ja parantaa päätöksiä.
joka keksi koulun
K. Mikä on nopein klusterointimenetelmä?
K-keskiarvoklusterointia pidetään usein nopeimpana klusterointimenetelmänä sen yksinkertaisuuden ja laskentatehokkuuden vuoksi. Se määrittää iteratiivisesti tietopisteet lähimpään klusterin keskipisteeseen, mikä tekee siitä sopivan suurille tietojoukoille, joilla on pieni ulottuvuus ja kohtalainen määrä klustereita.
K. Mitkä ovat klusteroinnin rajoitukset?
Klusteroinnin rajoituksia ovat herkkyys alkuolosuhteille, riippuvuus parametrien valinnasta, vaikeudet määrittää optimaalinen klusterimäärä ja haasteet suuriulotteisten tai kohinaisten tietojen käsittelyssä.
K. Mistä klusteroinnin tuloksen laatu riippuu?
Klusterointitulosten laatu riippuu tekijöistä, kuten algoritmin valinnasta, etäisyysmetriikasta, klusterien määrästä, alustusmenetelmästä, tietojen esikäsittelytekniikoista, klusterin arviointimittareista ja toimialueen tiedosta. Nämä elementit yhdessä vaikuttavat klusterointituloksen tehokkuuteen ja tarkkuuteen.
