NFA:lla voi olla nolla, yksi tai useampi kuin yksi liike tietystä tilasta tietyssä syötesymbolissa. NFA:lla voi olla myös NULL-siirtoja (liikkeit ilman syöttösymbolia). Toisaalta DFA:lla on yksi ja vain yksi siirto tietystä tilasta tietyllä syöttösymbolilla.

NFA:n muuntaminen DFA:ksi:

Vaihe 1: Muunna annettu NFA vastaavaksi siirtymätaulukoksi
Muuntaaksemme NFA:n vastaavaksi siirtymätaulukoksi meidän on lueteltava kaikki tilat, syöttösymbolit ja siirtymäsäännöt. Siirtymäsäännöt esitetään matriisina, jossa rivit edustavat nykyistä tilaa, sarakkeet edustavat syötesymbolia ja solut edustavat seuraavaa tilaa.

Vaihe 2: Luo DFA:n aloitustila
DFA:n aloitustila on joukko kaikkia mahdollisia NFA:n aloitustiloja. Tätä sarjaa kutsutaan NFA:n aloitustilan epsilon-sulkemiseksi. Epsilonin sulkeminen on joukko kaikkia tiloja, jotka voidaan saavuttaa aloitustilasta seuraamalla epsilonin (?) siirtymiä.

Vaihe 3: Luo DFA:n siirtymätaulukko
DFA:n siirtymätaulukko on samanlainen kuin NFA:n siirtymätaulukko, mutta yksittäisten tilojen sijaan rivit ja sarakkeet edustavat tilajoukkoja. Kullekin syötesymbolille siirtymätaulukon vastaava solu sisältää tilajoukon epsilonin sulkemisen, joka on saatu noudattamalla NFA:n siirtymätaulukon siirtymäsääntöjä.

Vaihe 4: Luo DFA:n lopulliset tilat
DFA:n lopulliset tilat ovat tilajoukkoja, jotka sisältävät vähintään yhden lopullisen tilan NFA:sta.

Vaihe 5: Yksinkertaista DFA
Edellisissä vaiheissa saatu DFA voi sisältää tarpeettomia tiloja ja siirtymiä. DFA:n yksinkertaistamiseksi voimme käyttää seuraavia tekniikoita:

• Poista tavoittamattomat tilat: tilat, joihin ei saada yhteyttä aloitustilasta, voidaan poistaa DFA:sta.
• Poista kuolleet tilat: DFA:sta voidaan poistaa tilat, jotka eivät voi johtaa lopulliseen tilaan.
• Yhdistä vastaavat tilat: tilat, joilla on samat siirtymäsäännöt kaikille syöttösymboleille, voidaan yhdistää yhdeksi tilaan.

Vaihe 6: Toista vaiheet 3-5, kunnes yksinkertaistaminen ei ole enää mahdollista
DFA:n yksinkertaistamisen jälkeen toistamme vaiheet 3–5, kunnes yksinkertaistaminen ei ole enää mahdollista. Lopullinen saatu DFA on minimoitu DFA, joka vastaa annettua NFA:ta.

Esimerkki: Harkitse seuraavaa NFA:ta kuvassa 1.

Seuraavassa on NFA:n eri parametrit. Q = { q0, q1, q2 } ? = ( a, b ) F = { q2 } ? (NFA:n siirtymätoiminto)

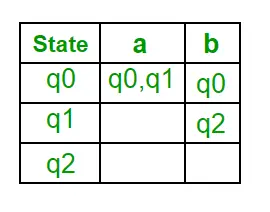
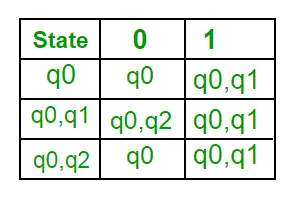
Vaihe 1: Q' = ? Vaihe 2: Q’ = {q0} Vaihe 3: Etsi kunkin syötesymbolin tilat kullekin Q':n tilalle. Tällä hetkellä Q':n tila on q0, etsi siirrot q0:sta syöttösymboleista a ja b käyttämällä NFA:n siirtymäfunktiota ja päivitä DFA:n siirtymätaulukko. ?’ (DFA:n siirtymäfunktio)

Nyt { q0, q1 } pidetään yhtenä tilana. Koska sen merkintä ei ole Q-kirjaimessa, lisää se kohtaan Q. Joten Q' = { q0, { q0, q1 } } Nyt siirtyy tilasta { q0, q1 } eri syöttösymboleilla ei ole DFA:n siirtymätaulukossa, laskemme sen seuraavasti: ?' , a ) = ? ( q0, a ) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0, b) ? ? ( q1, b ) = { q0, q2 } Nyt päivitetään DFA:n siirtymätaulukko. ?’ (DFA:n siirtymäfunktio)

Nyt { q0, q2 } pidetään yhtenä tilana. Koska sen merkintä ei ole Q-kirjaimessa, lisää se kohtaan Q. Joten Q' = { q0, { q0, q1 }, { q0, q2 } } Nyt siirrot tilasta {q0, q2} eri syöttösymboleilla eivät ole DFA:n siirtymätaulukossa, laskemme sen seuraavasti: ?' ( { q0, q2 }, a ) = ? ( q0, a ) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? ( q0, b ) ? ? ( q2, b ) = { q0 } Nyt päivitetään DFA:n siirtymätaulukko. ?’ (DFA:n siirtymäfunktio)

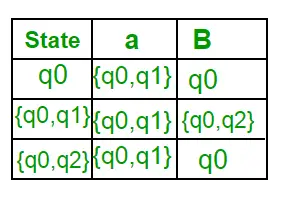
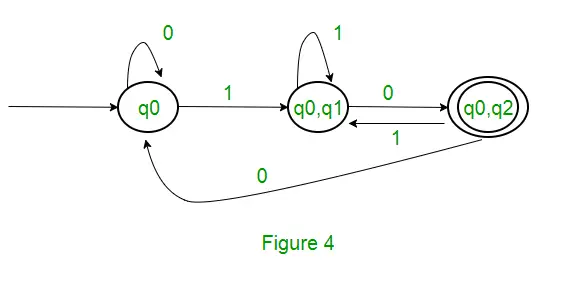
Koska uutta tilaa ei ole luotu, muunnos on valmis. DFA:n lopullinen tila on tila, jonka komponenttina on q2, eli { q0, q2 } Seuraavassa on DFA:n eri parametrit. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } ja siirtymäfunktio ?' kuten yllä on esitetty. Yllä olevan NFA:n lopullinen DFA on esitetty kuvassa 2.

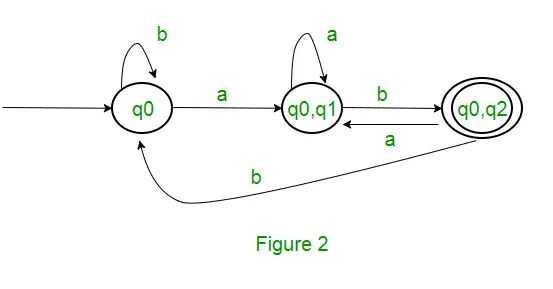
Huomautus : Joskus säännöllisen lausekkeen muuntaminen DFA:ksi ei ole helppoa. Ensin voit muuntaa säännöllisen lausekkeen NFA:ksi ja sitten NFA:n DFA:ksi.

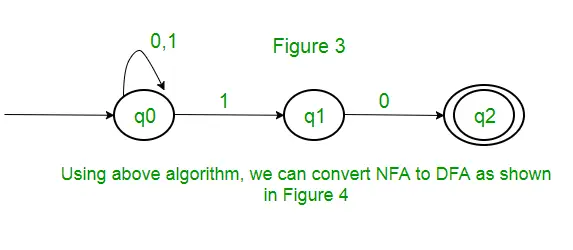
kysymys: Säännöllistä lauseketta (0 + 1)* (10) vastaavan minimideterministisen äärellisen automaatin tilojen lukumäärä on ____________.

Ratkaisu : Ensin tehdään NFA yllä olevalle lausekkeelle. Tehdäksemme NFA:n arvolle (0 + 1)*, NFA on samassa tilassa q0 syötesymbolilla 0 tai 1. Sitten ketjutusta varten lisäämme kaksi siirtoa (q0 arvoon q1 arvolle 1 ja q1 arvoon q2, kun arvo on 0) kuvan mukaisesti. kuvassa 3.

Tämän artikkelin on kirjoittanut Sonal Tuteja.