Lisäyslajittelu ja valintalajittelu ovat kaksi suosittua lajittelualgoritmia, ja niiden tärkein ero on siinä, kuinka ne valitsevat ja sijoittavat elementtejä lajiteltuun järjestykseen.
Valinnan lajittelu:
- Valintalajittelussa syöttötaulukko jaetaan kahteen osaan: lajiteltuun osaan ja lajittelemattomaan osaan.
- Algoritmi löytää toistuvasti lajittelemattoman osan minimielementin ja vaihtaa sen lajittelemattoman osan vasemmanpuoleisimman elementin kanssa laajentaen siten lajiteltua osaa yhdellä elementillä.
- Valintalajittelun aikamonimutkaisuus on O(n^2) kaikissa tapauksissa.
Lisäyslajittelu:
- Lisäyslajittelussa syöttötaulukko jaetaan myös kahteen osaan: lajiteltuun osaan ja lajittelemattomaan osaan.
Algoritmi poimii elementin lajittelemattomasta osasta ja sijoittaa sen oikeaan paikkaan lajiteltuun osaan siirtäen suuremmat elementit yhden paikan oikealle.
Lisäyslajittelun aikamonimutkaisuus on O(n^2) pahimmassa tapauksessa, mutta se voi toimia paremmin osittain lajiteltujen taulukoiden kanssa, kun parhaan tapauksen aikamonimutkaisuus on O(n).
Tärkeimmät erot: - Valintalajittelu skannaa lajittelemattoman osan löytääkseen minimielementin, kun taas lisäyslajittelu skannaa lajiteltua osaa löytääkseen oikean paikan elementin sijoittamiseen.
Valintalajittelu vaatii vähemmän vaihtoja kuin lisäyslajittelu, mutta enemmän vertailuja.
Lisäyslajittelu on tehokkaampaa kuin valintalajittelu, kun syöttötaulukko on osittain tai melkein lajiteltu, kun taas valintalajittelu toimii paremmin, kun taulukko on erittäin lajittelematon.
Yhteenvetona voidaan todeta, että molemmilla algoritmeilla on samanlainen aikamonimutkaisuus, mutta niiden valinta- ja sijoitusmenetelmät eroavat toisistaan. Valinta niiden välillä riippuu syöttötietojen ominaisuuksista ja käsiteltävän ongelman erityisvaatimuksista.
Lisäyslajittelun edut:
- Yksinkertainen ja helppo ymmärtää ja toteuttaa.
- Tehokas pienille tietojoukoille tai lähes lajiteltuihin tietoihin.
- Paikalla toimiva lajittelualgoritmi, eli se ei vaadi ylimääräistä muistia.
- Vakaa lajittelualgoritmi, eli se ylläpitää yhtäläisten elementtien suhteellista järjestystä syöttötaulukossa.
Lisäyslajittelun haitat:
- Tehoton suurille tietojoukoille tai käänteisen järjestyksen datalle, pahimman tapauksen aikamonimutkaisuuden ollessa O(n^2).
- Lisäyslajittelussa on paljon vaihtoja, mikä voi hidastaa sitä nykyaikaisissa tietokoneissa.
Valikoimalajittelun edut:
- Yksinkertainen ja helppo ymmärtää ja toteuttaa.
- Tehokas pienille tietojoukoille tai lähes lajiteltuihin tietoihin.
- Paikalla toimiva lajittelualgoritmi, eli se ei vaadi ylimääräistä muistia.
Valikoimalajittelun haitat:
- Tehoton suurille tietojoukoille, pahimman mahdollisen aikamonimutkaisuuden ollessa O(n^2).
- Valintalajittelussa on paljon vertailuja, mikä voi hidastaa sitä nykyaikaisissa tietokoneissa.
- Epävakaa lajittelualgoritmi, mikä tarkoittaa, että se ei välttämättä ylläpidä yhtäläisten elementtien suhteellista järjestystä syöttötaulukossa.
Tässä artikkelissa käsittelemme lisäyslajittelun ja valintalajittelun välistä eroa:
Lisäyslajittelu on yksinkertainen lajittelualgoritmi, joka toimii samalla tavalla kuin lajittelet pelikortit käsissäsi. Taulukko on käytännössä jaettu lajiteltuun ja lajittelemattomaan osaan. Lajittelemattoman osan arvot poimitaan ja sijoitetaan oikeaan kohtaan lajiteltuun osaan.
Algoritmi:
N-koon taulukon lajitteleminen nousevaan järjestykseen:
- Toisto arr[1]:stä arr[n]:iin taulukon yli.
- Vertaa nykyistä elementtiä (avainta) edeltäjäänsä.
- Jos avainelementti on pienempi kuin edeltäjänsä, vertaa sitä edellisiin elementteihin. Siirrä suurempia elementtejä yksi paikka ylöspäin, jotta vaihdetulle elementille tulee tilaa.
Alla on lisäyslajittelua havainnollistava kuva:
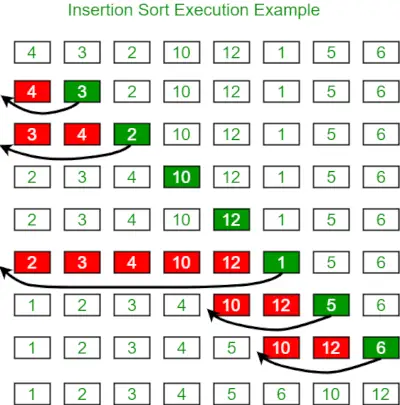
Alla on sama ohjelma:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> avain) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = avain; } } // Toiminto tulostaa taulukon, jonka koko on N void printArray(int arr[], int n) { int i; // Tulosta matriisi kohteelle (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> avain) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = avain; } } // Toiminto tulostaa N-koon taulukon static void printArray(int arr[], int n) { int i; // Tulosta matriisi kohteelle (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Ohjainkoodi public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; Tämän koodin tarjoaa code_hunt>> |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>>0> and>arr[j]>avain):>>arr[j>+>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> avain) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = avain; } } // Toiminto tulostaa N-koon taulukon static void printArray(int[] arr, int n) { int i; // Tulosta matriisi kohteelle (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Ohjainkoodi staattinen public void Main() { int[] arr = uusi int[] { 12, 11, 13, 5, 6 } int N = arr.Length; avustaja Dharanendra L V>>>
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> avain) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = avain; } } // Funktio tulostaa N-koon taulukon funktio printArray(arr,n) { let i; // Tulosta matriisi kohteelle (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Ohjainkoodi let arr=[12, 11 , 13, 5, 6]; anna N = arr.length // Funktio Call insertion(arr, N)>5 6 11 12 13> The valinta lajittelu Algoritmi lajittelee taulukon etsimällä toistuvasti (nousevassa järjestyksessä) minimielementin lajittelemattomasta osasta ja sijoittamalla sen alkuun. Algoritmi ylläpitää kahta alitaulukkoa tietyssä taulukossa.
- Alaryhmä on jo lajiteltu.
- Jäljellä oleva aliryhmä on lajittelematon.
Jokaisessa valintalajittelun iteraatiossa vähimmäiselementti (nousevassa järjestyksessä) poimitaan lajittelemattomasta alitaulukosta ja siirretään lajiteltuun alitaulukkoon.
Alla on esimerkki, joka selittää yllä olevat vaiheet:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Alla on sama ohjelma:
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Java
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python 3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
aritmeettinen logiikkayksikkö
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>Javascript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Lähtö:Sorted array: 11 12 22 25 64>Lisäyslajittelun ja valintalajittelun välinen taulukkoero:
Lisäys Lajittele Valinta Lajittele 1. Lisää arvon esilajiteltuun taulukkoon lajitellaksesi taulukon arvot. Etsii luettelosta vähimmäis-/maksimiluvun ja lajittelee sen nousevaan/laskevaan järjestykseen. 2. Se on vakaa lajittelualgoritmi. Se on epävakaa lajittelualgoritmi. 3. Parhaassa tapauksessa aikakompleksisuus on Ω(N), kun matriisi on jo nousevassa järjestyksessä. Siinä on Θ(N2) pahimmassa tapauksessa ja keskimääräisessä tapauksessa. Parhaassa tapauksessa pahimman tapauksen ja keskimääräisen valintalajittelun monimutkaisuus on Θ(N2). 4. Tässä lajittelualgoritmissa suoritettujen vertailuoperaatioiden määrä on pienempi kuin suoritettu vaihto. Tässä lajittelualgoritmissa suoritettujen vertailuoperaatioiden määrä on enemmän kuin suoritettu vaihto. 5. Se on tehokkaampi kuin Valinta-lajittelu. Se on vähemmän tehokas kuin lisäyslajittelu. 6. Tässä elementti tunnetaan etukäteen, ja etsimme oikeaa sijaintia niiden sijoittamiseen. Elementin sijoituspaikka on aiemmin tiedossa, etsimme lisättävän elementin kyseiseen kohtaan. 7. Lisäyslajittelua käytetään, kun:
- Taulukossa on pieni määrä elementtejä
- Jäljellä on vain muutama lajiteltava elementti
Valintalajittelua käytetään, kun
- Pieni lista on järjestettävä
- Vaihtohinnalla ei ole väliä
- Kaikkien elementtien tarkastus on pakollista
- Muistiin kirjoittamisen kustannuksilla on väliä kuten flash-muistissa (Swapien määrä on O(n) verrattuna kuplalajittelun O(n2)
8. Lisäyslajittelu on mukautuva eli tehokas tietojoukoille, jotka on jo olennaisesti lajiteltu: aika monimutkaisuus on O (kn) kun jokainen syötteen elementti on enintään k paikoissa pois lajittelupaikastaan Valintalajittelu on paikallaan oleva vertailulajittelualgoritmi
