Ford-Fulkerson-algoritmi on laajalti käytetty algoritmi virtausverkon maksimivirtausongelman ratkaisemiseksi. Maksimivirtausongelmaan kuuluu virtauksen enimmäismäärän määrittäminen, joka voidaan lähettää lähdepisteestä nielupisteeseen suunnatussa painotetussa graafissa, riippuen reunojen kapasiteettirajoituksista.
Algoritmi toimii iteratiivisesti etsimällä lisäyspolun, joka on polku lähteestä nielulle jäännösgraafissa, eli graafi, joka saadaan vähentämällä virta kunkin reunan kapasiteetista. Tämän jälkeen algoritmi lisää virtausta tällä reitillä suurimmalla mahdollisella määrällä, joka on reunojen pienin kapasiteetti.
Ongelma:
Annettu graafi, joka edustaa virtausverkkoa, jossa jokaisella reunalla on kapasiteetti. Lisäksi annetaan kaksi kärkeä lähde 's' ja pesuallas Etsi kaaviosta 't' suurin mahdollinen virtaus arvosta s paikkaan t seuraavilla rajoituksilla:
- Virtaus reunalla ei ylitä reunan annettua kapasiteettia.
- Tuleva virta on yhtä suuri kuin lähtevä virta jokaiselle pisteelle paitsi s ja t.
Harkitse esimerkiksi seuraavaa kuvaajaa CLRS-kirjasta.
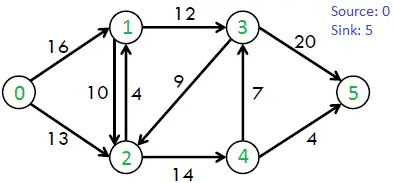
Suurin mahdollinen virtaus yllä olevassa kaaviossa on 23.

Edellytys: Max Flow -ongelman esittely
Ford-Fulkerson-algoritmi
Seuraava on yksinkertainen idea Ford-Fulkerson-algoritmista:
- Aloita alkuvirtauksella 0.
- Vaikka lähteestä nieluon on olemassa lisäyspolku:
- Etsi lisäävä polku käyttämällä mitä tahansa polunetsintäalgoritmia, kuten leveyshakua tai syvyyshakua.
- Määritä virtausmäärä, joka voidaan lähettää lisäysreittiä pitkin, mikä on pienin jäännöskapasiteetti polun reunoja pitkin.
- Lisää virtausta lisäysreitillä määritetyllä määrällä.
- Palauta maksimivirtaus.
Aika monimutkaisuus: Yllä olevan algoritmin aikamonimutkaisuus on O(max_flow * E). Suoritamme silmukan, kun on lisäyspolku. Pahimmassa tapauksessa saatamme lisätä 1 yksikkövirtauksen joka iteraatioon. Siksi aika monimutkaisuus muuttuu O(max_flow * E).
Kuinka toteuttaa yllä oleva yksinkertainen algoritmi?
Määritellään ensin jäännösgraafin käsite, jota tarvitaan toteutuksen ymmärtämiseen.
Jäännöskaavio virtausverkosto on kaavio, joka osoittaa mahdollisen lisävirtauksen. Jos jäännösgraafissa on polku lähteestä nieluun, on mahdollista lisätä virtaus. Jokaisella jäännösgraafin reunalla on arvo, jota kutsutaan jäännöskapasiteetti joka on yhtä suuri kuin reunan alkuperäinen kapasiteetti miinus virta. Jäännöskapasiteetti on pohjimmiltaan reunan nykyinen kapasiteetti.
Puhutaan nyt täytäntöönpanon yksityiskohdista. Jäännöskapasiteetti on 0, jos jäännösgraafin kahden kärjen välillä ei ole reunaa. Voimme alustaa jäännöskäyrän alkuperäiseksi kaavioksi, koska alkuvirtausta ei ole ja alun perin jäännöskapasiteetti on yhtä suuri kuin alkuperäinen kapasiteetti. Lisäyspolun löytämiseksi voimme joko tehdä jäännösgraafin BFS:n tai DFS:n. Olemme käyttäneet BFS:ää alla olevassa toteutuksessa. BFS:n avulla voimme selvittää, onko olemassa polku lähteestä nieluun. BFS rakentaa myös vanhempi[]-taulukon. Käyttämällä vanhempi[]-taulukkoa kuljemme löydetyn polun läpi ja löydämme mahdollisen virtauksen tämän polun läpi etsimällä polun varrelta vähimmäisjäännöskapasiteetin. Myöhemmin lisäämme löydetyn polun virtauksen kokonaisvirtaan.
Tärkeintä on, että meidän on päivitettävä jäännöskaavion jäännöskapasiteetit. Vähennämme polun virtauksen kaikista reunoista pitkin polkua ja lisäämme reitin virtauksen käänteisiä reunoja pitkin Meidän on lisättävä reitin virtaus käänteisiä reunoja pitkin, koska saattaa myöhemmin olla tarpeen lähettää virtaus vastakkaiseen suuntaan (katso esimerkiksi seuraava linkki).
kääntää merkkijono javassa
Alla on Ford-Fulkerson-algoritmin toteutus. Asioiden yksinkertaistamiseksi kuvaaja esitetään 2D-matriisina.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Jos löydämme yhteyden nielusolmuun, // niin BFS:ssä ei ole enää mitään järkeä. Meidän // täytyy vain asettaa sen emo ja voidaan palauttaa // true if (v == t) { iso[ v] = u; palauttaa tosi; } q.push(v); vanhempi[v] = u; vierailtu[v] = tosi; } } } // Emme saavuttaneet sinkiä BFS:ssä lähteestä alkaen, joten // return false return false; } // Palauttaa maksimivirtauksen arvosta s paikkaan t annetussa graafissa int fordFulkerson(int graafi[V][V], int s, int t) { int u, v; // Luo jäännösgraafi ja täytä jäännösgraafi // annetuilla kapasiteeteilla alkuperäisessä kaaviossa // jäännösgraafin jäännöskapasiteetit int rGraph[V] [V]; // Jäännösgraafi jossa rGraph[i][j] // osoittaa reunan jäännöskapasiteetin // välillä i - j (jos on reuna. Jos // rGraph[i][j] on 0, niin ei ole) for (u = 0; u for (v = 0; v rGraph[u][v] = kaavio[u][v]; int vanhempi[V]; // Tämän taulukon täyttää BFS ja // tallennuspolku int max_flow = 0 // Virtausta ei ole aluksi // Lisää virtausta, kun on polku lähteestä // uppoaa while (bfs(rGraph, s, t, parent)) { // Etsi reunojen vähimmäisjäännöskapasiteetti; pitkin // BFS:n täyttämää polkua tai voimme sanoa, että // löydetty polun läpi kulkeva maksimivirtaus = INT_MAX for (v = t; v != s; v = vanhempi[v] emo[v] emo[v]) { u = emo[v] - = polkuvirtaus [v][u] += polkuvirtaus += polkuvirtaus; // Palauttaa kokonaisvirran paluu max_flow; } // Ohjainohjelma yllä olevien funktioiden testaamiseen int main() { // Luodaan kaavio, joka näkyy yllä olevassa esimerkissä int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Jos löydämme yhteyden nielun // solmuun, niin BFS:ssä // ei ole enää mitään järkeä Meidän on vain asetettava sen pää // ja se voidaan palauttaa tosi jos (v == t) { vanhempi[ v] = u; palauttaa tosi; } queue.add(v); vanhempi[v] = u; vierailtu[v] = tosi; } } } // Emme saavuttaneet sinkiä BFS:ssä lähteestä alkaen, // joten return false return false; } // Palauttaa maksimivirtauksen arvosta s paikkaan t annetussa kaaviossa // int fordFulkerson(int graph[][], int s, int t) { int u, v; // Luo jäännösgraafi ja täytä jäännöskaavio alkuperäisen graafin annetuilla kapasiteeteilla // jäännöskaavion jäännöskapasiteeteina // Jäännösgraafi jossa rGraph[i][j] osoittaa // reunan jäännöskapasiteetti välillä i j (jos // on reuna. Jos rGraph[i][j] on 0, silloin // ei ole) int rGraph[][] = uusi int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = kaavio[u][v]; // Tämän taulukon täyttää BFS ja tallentaa polun int parent[] = new int[ V] int max_flow = 0 // Virtausta ei ole aluksi // Lisää virtausta, kun on polku lähteestä // uppoamaan while (bfs(rGraph, s, t, parent)) { // Etsi pienin jäännöskapasiteetti; reunoista // BFS:n täyttämää polkua pitkin. Tai voidaan sanoa, että // löydetty polun läpi kulkeva maksimivirtaus. MAX_VALUE for (v = t; v ! = s; ]) { u = polkuvirtaus = Math.min(polkuvirtaus, rGraph[u][v] } // päivitä reunojen jäännöskapasiteetit ja // reunoja pitkin polkua (v = t; v != s; v = vanhempi[v] - rGraph[v][u] += polkuvirtaus; flow max_flow += polkuvirtaus } // Palauttaa kokonaisvirran paluu max_flow; yllä olevassa esimerkissä int-kaavio[][] = uusi int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = uusi MaxFlow(); System.out.println('Suurin mahdollinen virtaus on ' + m.fordFulkerson(kaavio, 0, 5)); } }> |
>
näkymät ja pöydät
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
c#-kytkin
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
vertailukelpoinen käyttöliittymä javassa
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Jos löydämme yhteyden nielun // solmuun, niin BFS:ssä // ei ole enää mitään järkeä Meidän on vain asetettava sen pää // ja se voidaan palauttaa tosi jos (v == t) { vanhempi[ v] = u; palauttaa tosi; } queue.push(v); vanhempi[v] = u; vierailtu[v] = tosi; } } } // Emme saavuttaneet sinkiä BFS:ssä alkaen // lähteestä, joten return false return false; } // Palauttaa maksimivirtauksen arvosta s paikkaan t // annetussa graafifunktiossa fordFulkerson(graph, s, t) { anna u, v; // Luo jäännösgraafi ja täytä // jäännöskäyrä annetuilla kapasiteeteilla // alkuperäisessä kaaviossa jäännöskuvaajan kapasiteetit // jäännöskaavio, jossa rGraph[i][j] // osoittaa reunan jäännöskapasiteetin // / i:stä j:hen (jos on reuna. // Jos rGraph[i][j] on 0, niin ei ole // ei) olkoon rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Tämä taulukko täyttää BFS ja tallentaa polku let parent = new Array(V) // Ei ole virtaa aluksi anna max_flow = 0 // Lisää virtausta, kun siellä on polku lähteestä nieluun while (bfs(rGraph, s, t); , emo)) { // Etsi BFS:n täyttämää polkua pitkin olevien reunojen minimikapasiteetti v != s; v = vanhempi[v] käänteiset reunat polulla for(v = t; v != s; v = vanhempi[v]) { u = vanhempi[v] - = polkuvirtaus [v][u] +; = polkuvirtaus } // Lisää polkuvirtaus kokonaisvirtaukseen , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ]]; document.write('Suurin mahdollinen virtaus on ' + fordFulkerson(kaavio, 0, 5)); // Tämän koodin tarjoaa avanitrachhadiya2155>> |
>The maximum possible flow is 23>
Aika monimutkaisuus : O(|V| * E^2) ,jossa E on reunojen lukumäärä ja V on kärkien lukumäärä.
Tilan monimutkaisuus:O(V), kun loimme jonon.
Yllä olevaa Ford Fulkerson -algoritmin toteutusta kutsutaan Edmonds-Karp -algoritmi . Edmonds-Karpin ideana on käyttää BFS:ää Ford Fulkerson -toteutuksessa, koska BFS valitsee aina polun, jolla on mahdollisimman vähän reunoja. Kun käytetään BFS:ää, pahimman tapauksen ajan monimutkaisuus voidaan vähentää arvoon O(VE2). Yllä oleva toteutus käyttää viereisyysmatriisiesitystä, vaikka BFS ottaa O(V2) aika, yllä olevan toteutuksen aikamonimutkaisuus on O(EV3) (Viitata CLRS kirja todiste ajan monimutkaisuudesta)
Tämä on tärkeä ongelma, koska se ilmenee monissa käytännön tilanteissa. Esimerkkejä ovat kuljetuksen maksimoiminen tietyillä liikennerajoilla, pakettivirran maksimoiminen tietokoneverkoissa.
Dincin algoritmi Max-Flow:lle.
Harjoittele:
Muokkaa yllä olevaa toteutusta niin, että se toimii O(VE2) aika.
