A Ohjattu asyklinen kaavio , usein lyhennettynä PÄIVÄ , on graafiteorian peruskäsite. DAG:t käytetään osoittamaan, miten asiat liittyvät toisiinsa tai riippuvat toisistaan ​​selkeästi ja järjestelmällisesti. Tässä artikkelissa aiomme oppia Ohjattu asyklinen kaavio , sen ominaisuudet ja käyttö tosielämässä.

Ohjattu asyklinen kaavio

Mikä on suunnattu asyklinen graafi?

A Ohjattu asyklinen kaavio (DAG) on suunnattu graafi, joka ei sisällä jaksoja.

Alla oleva kaavio edustaa suunnattua asyklistä kuvaajaa (DAG):

Suora asyklinen kaavio

Suunnatun asyklisen graafin merkitys:

Ohjatulla Asyklisellä Graphilla on kaksi tärkeää ominaisuutta:

• Ohjannut Edge s:Ohjatussa asyklisessä kaaviossa jokaisella reunalla on suunta, eli se kulkee yhdestä kärjestä (solmupisteestä) toiseen. Tämä suunta merkitsee a yksisuuntainen solmujen välinen suhde tai riippuvuus.
• Asyklinen: Termi asyklinen osoittaa, että kaaviossa ei ole jaksoja tai suljettuja silmukoita. Toisin sanoen et voi kulkea suunnattujen reunojen sarjaa ja palata samaan solmuun reunasuuntia noudattaen. Jaksojen muodostus on kielletty PÄIVÄ. Siksi tämä ominaisuus on välttämätön.

Ohjattu asyklinen kaavio

Suunnatun asyklisen graafin DAG ominaisuudet:

Suunnatulla Asyklisellä Graphilla (DAG) on erilaisia ​​ominaisuuksia, jotka tekevät niistä käyttökelpoisia kuvaajaongelmissa.

Directed Acyclic Graph (DAG) sisältää seuraavat ominaisuudet:

• Saavutettavuussuhde: DAG:ssa voimme määrittää, onko kahden solmun välillä saavutettavuussuhde. Solmun A sanotaan olevan tavoitettavissa solmusta B, jos on olemassa suunnattu polku, joka alkaa solmusta B ja päättyy solmuun A. Tämä tarkoittaa, että voit seurata graafin reunojen suuntaa päästäksesi B:stä A:han.
• Transitiivinen sulkeminen: Suunnatun graafin transitiivinen sulkeminen on uusi graafi, joka edustaa kaikkia suoria ja epäsuoria suhteita tai yhteyksiä solmujen välillä alkuperäisessä graafissa. Toisin sanoen se kertoo, mitkä solmut voidaan saavuttaa muista solmuista seuraamalla yhtä tai useampaa suunnattua reunaa.

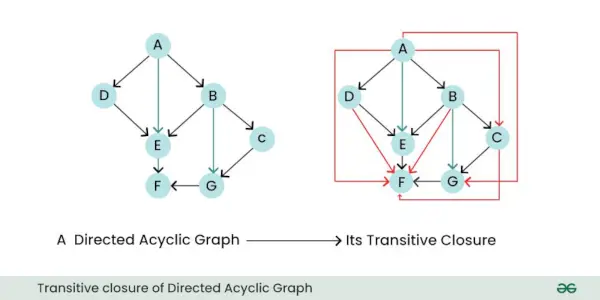
Suunnatun asyklisen graafin transitiivinen sulkeminen

• Transitiivinen vähennys: Suunnatun graafin transitiivinen pelkistys on uusi graafi, joka säilyttää vain olennaiset suorat suhteet solmujen välillä ja poistaa kaikki tarpeettomat epäsuorat reunat. Pohjimmiltaan se yksinkertaistaa kuvaajaa poistamalla reunat, jotka voidaan päätellä muista reunoista.

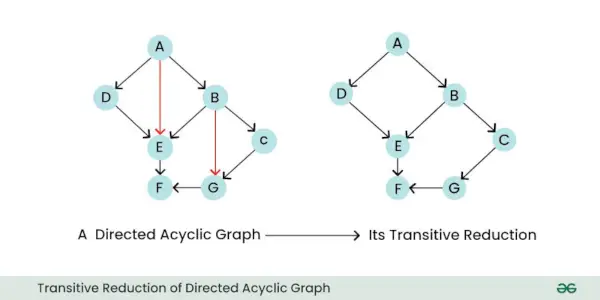
Suunnatun asyklisen graafin transitiivinen pelkistys

• Topologinen järjestys: DAG voidaan lajitella topologisesti, mikä tarkoittaa, että voit järjestää sen solmut lineaarisesti siten, että kaikilla reunoilla reunan aloitussolmu esiintyy aikaisemmin sarjassa. Tämä ominaisuus on hyödyllinen tehtäviin, kuten ajoitukseen ja riippuvuuden selvittämiseen.

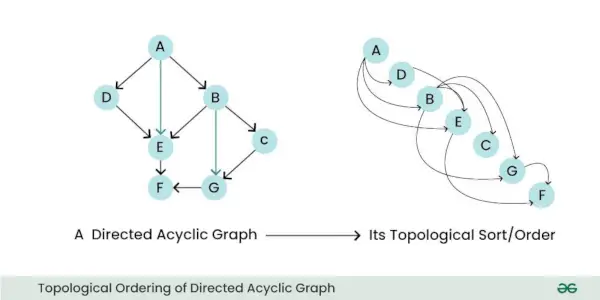
Suunnatun asyklisen graafin topologinen järjestys

DAG:n käytännön sovellukset:

• Tietovirran analyysi: Kääntäjän suunnittelussa ja optimoinnissa DAG:ita käytetään kuvaamaan tietovirtaa ohjelman sisällä. Tämä auttaa optimoimaan koodia tunnistamalla ylimääräiset laskelmat ja kuolleen koodin. DAG:ita käytetään myös edustamaan rakennetta peruslohkot Kääntäjän suunnittelussa.

• Tehtävän aikataulutus: DAG:ita käytetään projektinhallinnassa ja työn aikataulutuksessa. Jokainen tehtävä tai työ esitetään solmuna DAG:ssa, ja suunnatut reunat osoittavat riippuvuuksia. DAG:n asyklinen luonne varmistaa, että tehtävät ajoitetaan loogiseen järjestykseen, mikä estää pyöreät riippuvuudet.

Painotettua suunnattua asyklistä kuvaajaa voidaan käyttää esittämään ajoitusongelmaa. Otetaan esimerkki tehtävän ajoitusongelmasta. Tässä kärkipiste voi edustaa tehtävää ja sen paino voi edustaa tehtävän laskennan kokoa. Samoin reuna voi edustaa kahden tehtävän välistä viestintää ja sen paino voi edustaa viestinnän kustannuksia:

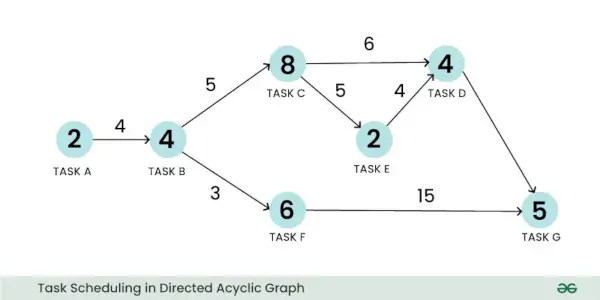
Tehtävien ajoitus suunnatussa asyklisessä kaaviossa

Johtopäätös:

Yhteenvetona voidaan todeta, että suunnatut asykliset graafit ovat graafiteorian peruskäsite, jolla on lukuisia käytännön sovelluksia. DAG:illa on keskeinen rooli tehtävien ajoituksessa, tietovirran analysoinnissa, riippuvuuden selvittämisessä ja monilla muilla tietojenkäsittelytieteen ja tekniikan aloilla. Ne auttavat optimoimaan prosesseja, hallitsemaan riippuvuuksia ja varmistamaan tehtävien tai töiden tehokkaan suorittamisen.