Peter Chen kehitti ER-kaavion vuonna 1976. ER-malli luotiin tarjoamaan yksinkertainen ja ymmärrettävä malli tietokantojen rakenteen ja logiikan esittämiseksi. Siitä on sittemmin kehittynyt muunnelmia, kuten Enhanced ER Model ja Object Relationship Model

Entiteettirelaatiomalli on malli, jolla tunnistetaan tietokannassa esitettävät entiteetit ja esitetään, kuinka kyseiset entiteetit liittyvät toisiinsa. ER-tietomalli määrittää yritysskeeman, joka edustaa tietokannan loogista kokonaisrakennetta graafisesti.

Entity Relationship Diagram selittää tietokannassa olevien entiteettien välisen suhteen. ER-malleja käytetään todellisten esineiden, kuten henkilön, auton tai yrityksen, ja näiden reaalimaailman objektien välisen suhteen mallintamiseen. Lyhyesti sanottuna ER-kaavio on tietokannan rakennemuoto.

Miksi käyttää ER-kaavioita DBMS:ssä?

• ER-kaavioita käytetään E-R-mallin esittämiseen tietokannassa, mikä tekee niistä helposti muunnettavissa suhteiksi (taulukoiksi).
• ER-kaaviot tarjoavat kohteen reaalimaailman mallintamiseen, mikä tekee niistä erittäin hyödyllisiä.
• ER-kaaviot eivät vaadi teknistä tietoa eikä laitteistotukea.
• Nämä kaaviot ovat erittäin helposti ymmärrettäviä ja helppoja luoda jopa naiiville käyttäjälle.
• Se tarjoaa standardiratkaisun tietojen visualisointiin loogisesti.

ER-mallissa käytetyt symbolit

ER-mallia käytetään mallintamaan järjestelmän loogista näkymää dataperspektiivistä, joka koostuu seuraavista symboleista:

• Suorakulmiot: Suorakulmiot edustavat entiteettejä ER-mallissa.
• Ellipsit: Ellipsit edustavat attribuutteja ER-mallissa.
• Timantti: Timantit edustavat entiteettien välisiä suhteita.
• Rivit: Viivat edustavat entiteettien attribuutteja ja entiteettijoukkoja, joilla on muita suhdetyyppejä.
• Kaksoisellipsi: Kaksoisellipsit edustavat Moniarvoiset attribuutit .
• Kaksinkertainen suorakaide: Kaksoissuorakulmio edustaa heikkoa kokonaisuutta.

ER-kaaviossa käytetyt symbolit

ER-kaavion osat

ER-malli koostuu kokonaisuuksista, attribuuteista ja entiteettien välisistä suhteista tietokantajärjestelmässä.

ER-kaavion osat

Entiteetti

Entiteetti voi olla esine, jolla on fyysinen olemassaolo – tietty henkilö, auto, talo tai työntekijä – tai se voi olla esine, jolla on käsitteellinen olemassaolo – yritys, työ tai yliopistokurssi.

Entiteettiä on kahta tyyppiä

1. Aineellinen kokonaisuus - Jota voidaan koskea, kuten autoa, henkilöä jne.

2. Ei-aineellinen kokonaisuus - Mihin ei voi koskea, kuten ilmaan, pankkitiliin jne.

kevät saappaat

Entiteettijoukko: Entiteetti on entiteettityypin objekti ja kaikkien entiteettien joukkoa kutsutaan entiteettijoukoksi. Esimerkiksi E1 on entiteetti, jolla on Entity Type Student, ja kaikkien opiskelijoiden joukkoa kutsutaan Entity Set. ER-kaaviossa entiteettityyppi esitetään seuraavasti:

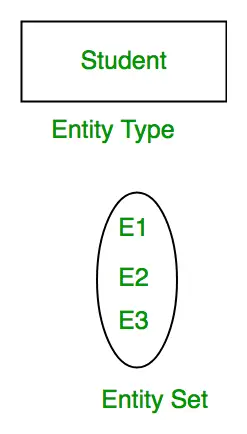
Entiteettijoukko

Voimme edustaa ER-kaaviossa asetettua entiteettiä, mutta emme voi edustaa entiteettiä ER-kaaviossa, koska entiteetti on suhteessa rivi ja sarake ja ER-kaavio on tietojen graafinen esitys.

1. Vahva entiteetti

A Vahva entiteetti on entiteettityyppi, jolla on avainattribuutti. Vahva entiteetti ei ole riippuvainen skeeman toisesta entiteetistä. Siinä on ensisijainen avain, joka auttaa tunnistamaan sen yksilöllisesti, ja sitä edustaa suorakulmio. Näitä kutsutaan vahvoiksi entiteettityypeiksi.

2. Heikko entiteetti

Entiteettityypillä on avainattribuutti, joka yksilöi yksilöllisesti jokaisen entiteettijoukon entiteetin. Mutta on olemassa jokin entiteettityyppi, jolle ei voida määrittää avainattribuutteja. Näitä kutsutaan Heikot entiteettityypit .

Esimerkiksi, Yritys voi tallentaa työntekijän huollettavien (vanhemmat, lapset, puoliso) tiedot. Mutta huollettavat eivät voi olla olemassa ilman työntekijää. Joten riippuvainen tulee olemaan a Heikko entiteettityyppi ja Työntekijä on Dependentin tunnistekokonaisuuden tyyppi, mikä tarkoittaa, että se on Vahva entiteettityyppi .

Heikkoa entiteettityyppiä edustaa kaksoissuorakulmio. Heikkojen entiteettityyppien osallistuminen on aina täydellistä. Heikon entiteettityypin ja sen tunnistavan vahvan entiteettityypin välistä suhdetta kutsutaan tunnistavaksi suhteeksi ja sitä edustaa kaksoistimantti.

Vahva entiteetti ja heikko entiteetti

Attribuutit

Attribuutit ovat ominaisuuksia, jotka määrittävät entiteettityypin. Esimerkiksi Roll_No, Name, DOB, Age, Address ja Mobile_No ovat attribuutit, jotka määrittävät entiteettityypin Opiskelija. ER-kaaviossa attribuuttia edustaa soikea.

Attribuutti

1. Avainmäärite

Attribuutti, joka yksilöi jokaisen kokonaisuuden yksilöllisesti entiteettijoukossa kutsutaan avainattribuutiksi. Esimerkiksi Roll_No on yksilöllinen jokaiselle opiskelijalle. ER-kaaviossa avainattribuuttia edustaa soikea, jonka alla on viivoja.

Key Attribuutti

2. Yhdistelmämäärite

Attribuutti koostuu monista muista ominaisuuksista kutsutaan yhdistelmäattribuutiksi. Esimerkiksi opiskelijaentiteettityypin Address-attribuutti koostuu Streetistä, kaupungista, osavaltiosta ja maasta. ER-kaaviossa yhdistelmäattribuuttia edustaa soikea, joka koostuu soikeista.

Komposiittiattribuutti

3. Moniarvoinen attribuutti

Attribuutti, joka koostuu useammasta kuin yhdestä arvosta tietylle entiteetille. Esimerkiksi Phone_No (voi olla useampi kuin yksi tietylle opiskelijalle). ER-kaaviossa moniarvoista attribuuttia edustaa kaksoisovaali.

Moniarvoinen attribuutti

4. Johtettu attribuutti

Attribuutti, joka voidaan johtaa entiteettityypin muista attribuuteista, tunnetaan johdettuna attribuuttina. esim.; Ikä (voidaan johtaa DOB:sta). ER-kaaviossa johdettu attribuutti on esitetty katkoviivalla soikealla.

Johdettu attribuutti

Täydellinen entiteettityypin opiskelija attribuuteineen voidaan esittää seuraavasti:

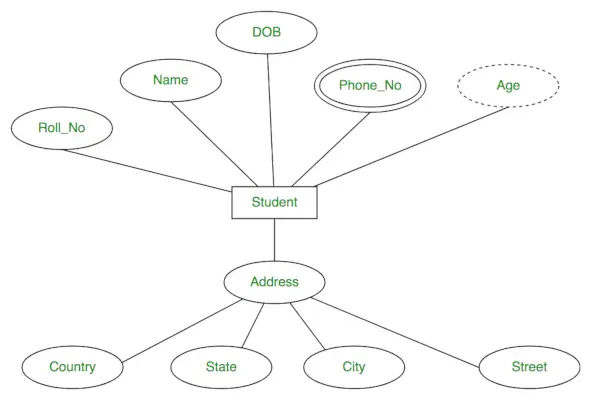
Entiteetti ja attribuutit

Suhteen tyyppi ja suhdesarja

Suhdetyyppi edustaa entiteettityyppien välistä yhteyttä. Esimerkiksi 'Rekisteröity' on suhdetyyppi, joka on entiteettityypin Student ja Course välillä. ER-kaaviossa suhdetyyppiä edustaa timantti, joka yhdistää entiteetit viivoilla.

Entiteetti-suhdesarja

setit javassa

Joukko samantyyppisiä suhteita tunnetaan suhdejoukona. Seuraava suhdejoukko kuvaa S1:tä C2:ssa, S2:ta C1:ssä ja S3:ta C3:ssa.

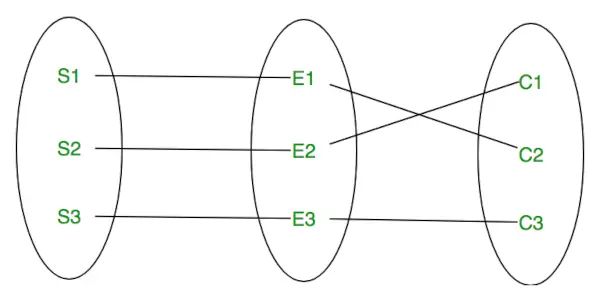
Suhdesarja

Suhdesarjan tutkinto

Suhdejoukkoon osallistuvien eri entiteettijoukkojen lukumäärää kutsutaan nimellä suhdejoukon aste.

1. Yksittäinen suhde: Kun suhteeseen osallistuu vain YKSI entiteettijoukko, suhdetta kutsutaan unaarisuhteeksi. Esimerkiksi yksi henkilö on naimisissa vain yhden henkilön kanssa.

Yksinäinen suhde

2. Binäärisuhde: Kun suhteeseen osallistuu KAKSI entiteettiä, suhdetta kutsutaan binäärisuhteeksi. Esimerkiksi opiskelija on ilmoittautunut kurssille.

Binäärisuhde

3. Kolminkertainen suhde: Kun relaatioon osallistuu n entiteettiä, suhdetta kutsutaan n-aariseksi suhteeksi.

Kardinaalisuus

Kuinka monta kertaa entiteettijoukon entiteetti osallistuu suhdejoukkoon, kutsutaan nimellä kardinaalisuus . Kardinaalisuus voi olla erityyppistä:

vertaa merkkijonossa

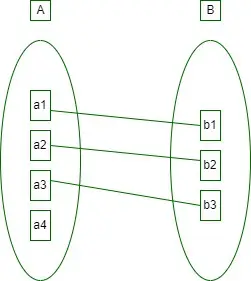
1. Yksittäinen: Kun jokainen entiteetti jokaisessa entiteettijoukossa voi osallistua suhteeseen vain kerran, kardinaliteetti on yksi yhteen. Oletetaan, että mies voi mennä naimisiin yhden naisen kanssa ja nainen yhden miehen kanssa. Joten suhde tulee olemaan yksi yhteen.

tässä käytettävien taulukoiden kokonaismäärä on 2.

yksi yhteen kardinaliteetti

Settiä käyttämällä se voidaan esittää seuraavasti:

Aseta yksi-yhteen esitys

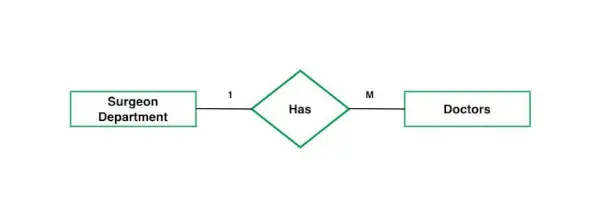
2. Yksi monille: Myös yhdestä moneen -kartoituksessa, jossa jokainen kokonaisuus voi liittyä useampaan kuin yhteen kokonaisuuteen ja tässä käytettävien taulukoiden kokonaismäärä on 2. Oletetaan, että yhdelle kirurgin osastolle mahtuu monta lääkäriä. Kardinaalisuus on siis 1:stä M. Se tarkoittaa, että yhdellä osastolla on monta lääkäriä.

käytettävien taulukoiden kokonaismäärä on 3.

kardinaliteetti yhdestä moneen

Joukkoja käyttämällä yksi-moneen kardinaliteetti voidaan esittää seuraavasti:

Aseta yksi-moneen esitys

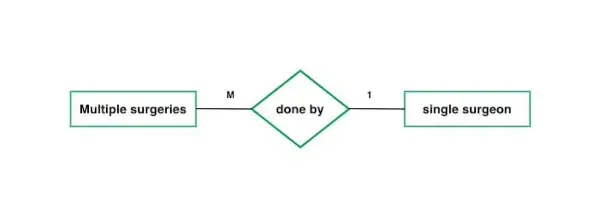
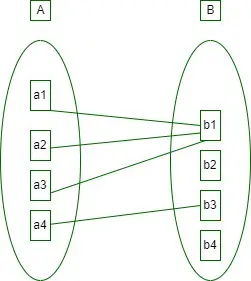
3. Useita yhteen: Kun yhden entiteettijoukon entiteetit voivat osallistua suhdejoukkoon vain kerran ja muiden entiteettijoukkojen entiteetit voivat osallistua useammin kuin kerran suhdejoukkoon, kardinaalisuus on monta yhteen. Oletetaan, että opiskelija voi suorittaa vain yhden kurssin, mutta yhden kurssin voi suorittaa useita opiskelijoita. Kardinaalisuus on siis n:stä 1:een. Se tarkoittaa, että yhdellä kurssilla voi olla n opiskelijaa, mutta yhdellä opiskelijalla on vain yksi kurssi.

Tässä käytettävien taulukoiden kokonaismäärä on 3.

monet yhteen kardinaalisuuteen

Settiä käyttämällä se voidaan esittää seuraavasti:

Aseta useiden yhteen esitys

Tässä tapauksessa jokainen opiskelija suorittaa vain yhden kurssin, mutta yhden kurssin on suorittanut monet opiskelijat.

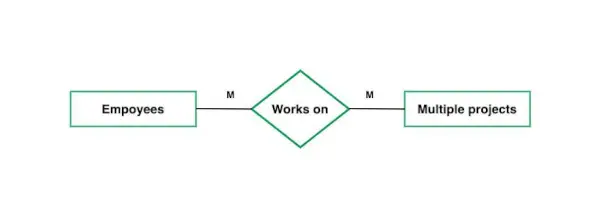
4. Monista moneen: Kun entiteetit kaikissa entiteettijoukkoissa voivat osallistua suhteeseen useammin kuin kerran, kardinaalisuus on monta moneen. Oletetaan, että opiskelija voi suorittaa useamman kuin yhden kurssin ja yhden kurssin voi suorittaa useita opiskelijoita. Joten suhde tulee olemaan monta moniin.

tässä käytettävien taulukoiden kokonaismäärä on 3.

monista moniin kardinaalisuutta

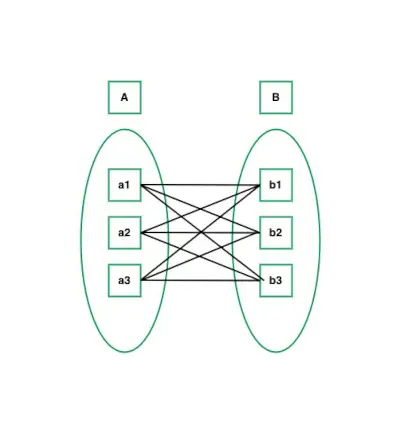
Settiä käyttämällä se voidaan esittää seuraavasti:

Useista moneen joukkoon -esitys

Tässä esimerkissä opiskelija S1 on ilmoittautunut kursseille C1 ja C3 ja kurssille C3 on ilmoittautunut S1, S3 ja S4. Kyse on siis monesta moneen suhteesta.

Osallistumisrajoitus

Osallistumisrajoitus sovelletaan suhdejoukkoon osallistuvaan kokonaisuuteen.

1. Kokonaisosallistuminen – Jokainen entiteettijoukon entiteetti täytyy osallistua suhteeseen. Jos jokaisen opiskelijan on ilmoittaututtava kurssille, opiskelijoiden osallistuminen on yhteensä. Kokonaisosallistuminen näkyy kaksoisviivalla ER-kaaviossa.

2. Osittainen osallistuminen – Entiteettijoukon entiteetti voi osallistua suhteeseen tai EI. Mikäli yksikään opiskelijoista ei ole ilmoittautunut joillekin kursseille, osallistuminen kurssille on osittainen.

gigatavu vs megatavu

Kaavio kuvaa Ilmoittautuneiden suhdejoukon opiskelijakokonaisuuksien kanssa, joilla on kokonaisosallistuminen, ja Kurssikokonaisuuksien joukkoon, jolla on osittainen osallistuminen.

Kokonaisosallistuminen ja osittainen osallistuminen

Setiä käyttämällä se voidaan esittää muodossa

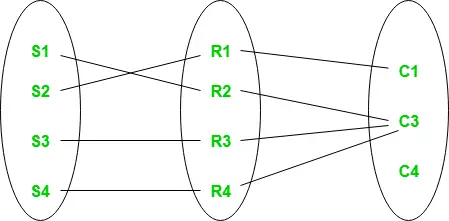
Aseta kokonaisosuuden ja osittaisen osallistumisen esitys

Jokainen opiskelijakokonaisuuden opiskelija osallistuu suhteeseen, mutta on olemassa kurssi C4, joka ei osallistu suhteeseen.

Kuinka piirtää ER-kaavio?

• Aivan ensimmäinen askel on tunnistaa kaikki entiteetit, sijoittaa ne suorakulmioon ja merkitä ne vastaavasti.
• Seuraava askel on tunnistaa niiden välinen suhde ja sijoittaa ne vastaavasti timantin avulla ja varmistaa, että suhteet eivät ole yhteydessä toisiinsa.
• Liitä attribuutit entiteeteihin oikein.
• Poista tarpeettomat kokonaisuudet ja suhteet.
• Lisää oikeat värit korostaaksesi tietokannassa olevat tiedot.