Onko jokainen suorakulmio rombi? Suorakaide on kaksiulotteinen geometrinen hahmo, joka on kuvattu neljällä sivulla ja neljällä kulmalla. Suorakulmiossa on sivut siten, että vastakkaisten sivujen pituus on yhtä suuri ja nämä sivut ovat yhdensuuntaisia keskenään. Sivut jakavat kulman vierekkäisistä sivuista, ja niiden välinen kulma on 90°. Siksi suorakulmiossa on neljä suoraa kulmaa.

Sisällysluettelo
- Suorakulmio
- Rombi
- Onko jokainen suorakulmio rombi?
- Esimerkkikysymykset – Onko jokainen suorakulmio rombi
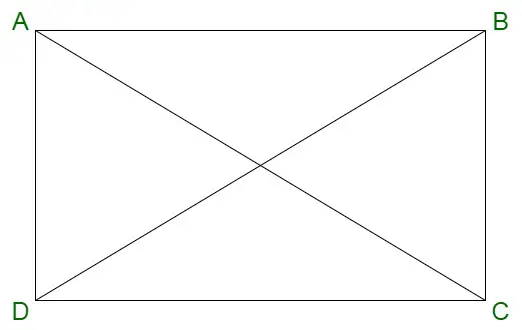
Suorakulmio
Suorakulmion ominaisuudet on annettu alla:
- Siinä on neljä reunaa ja neljä kulmaa, jotka tunnetaan nimellä kärkipisteet.
- Suorakulmion diagonaalit jakavat toisensa.
- Suorakulmion pinta-ala vastaa sen pituuden ja leveyden tuloa.
- Jokaisen kärjen kulma on 90O
- Suorakulmion vastakkaiset sivut ovat yhtä suuret ja yhdensuuntaiset toistensa kanssa.
- Kehä vastaa kaksi kertaa sen pituuden ja leveyden summaa.
- Kaikkien sisäkulmien summa on 360 astetta
Suorakulmion kehä
Kokonaissiirtymää, joka kattaa suorakulmion rajan läpi menemisen, voidaan kutsua kehäksi. Koska sekä pituus että leveys on merkitty pituuden yksikkönä, myös ympärysmitta mitataan pituuden yksikkönä.
Kehä voidaan merkitä,
Kehä, P = 2 (pituus + leveys)
Suorakulmion alue
Kaksiulotteisen geometrisen kuvion peittämää aluetta tasossa kutsutaan kuvion alueeksi. Siten suorakulmion pinta-ala on sen rajojen sisällä oleva alue. Se mitataan neliöyksiköissä. Pinta-ala vastaa suorakulmion pituuden ja leveyden tuloa.
Aluetta voidaan merkitä
Pinta-ala, A = pituus × leveys neliöyksikköä
Suorakaidekaavan lävistäjä
Minkä tahansa geometrisen hahmon diagonaalit yhdistävät vaihtoehtoiset kärjet. Suorakulmion diagonaalien pituus voidaan laskea seuraavalla kaavalla, jota merkitään d:llä,
d = sqrt{( l^2 + w^2)} missä,
l = suorakulmion pituus
w = suorakulmion leveys
Lue tarkemmin: Suorakulmion ominaisuudet: määritelmä, kaavat, esimerkit
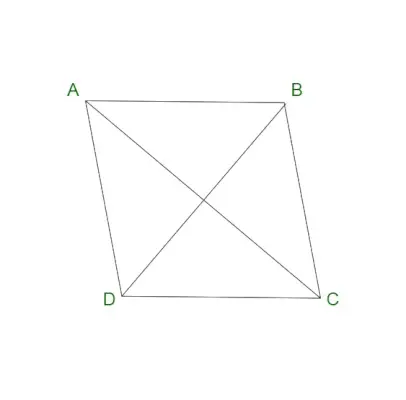
Rombi
Rombi tunnetaan myös nelisivuisena nelikulmiona. Sitä pidetään suunnikkaan erikoistapauksena. Rombissa on yhdensuuntaiset vastakkaiset sivut ja yhtä suuret vastakkaiset kulmat. Rombi tunnetaan myös nimellä timantti tai rombitimantti. Rombissa on rombin kaikki sivut yhtä pitkiä. Myös rombin lävistäjät jakavat toisensa suorassa kulmassa.
Rombin ominaisuudet
Rombi sisältää seuraavat ominaisuudet:
- Rombissa on kaikki yhtäläiset sivut.
- Rombin diagonaalit jakavat toisensa suorassa kulmassa.
- Rombin vastakkaiset sivut ovat luonteeltaan yhdensuuntaiset.
- Rombin kahden vierekkäisen kulman summa on 180O.
- Rombissa ei ole piirrettävää ympyrää.
- Rombin ympärillä ei ole ympyrää.
- Rombin diagonaalit johtavat neljän suorakulmaisen kolmion muodostumiseen.
- Nämä kolmiot ovat yhteensopivia keskenään.
- Rombin vastakkaiset kulmat ovat yhtä suuret.
- Kun yhdistät rombin sivujen keskipisteen, muodostuu suorakulmio.
- Kun puolikkaan diagonaalin keskipisteet yhdistetään, muodostuu toinen rombi.
Rombuksen ympärysmitta
Rombin ympärysmitta määritellään sen kuvion muodostavien rajojen kokonaispituudeksi. Sitä voidaan myös ilmaista rombin neljän sivun pituuden kokonaissummana. Rombin ympärysmitta määritellään seuraavasti:
Kehä, P = 4a yksikköä
jossa rombin diagonaalit on merkitty d:llä1& d2ja 'a' on puoli.
Rombuksen alue
Rombin pinta-ala määritellään alueeksi, joka on suljettu kaksiulotteisen tason sisällä. Rombin pinta-ala vastaa rombin diagonaalien tuloa jaettuna kahdella. Rombin pinta-ala voidaan määrittää seuraavalla kaavalla:
Alue, A =
frac{(d_1 imes d_2)}{2} neliöyksikköämissä D1ja d2ovat rombin lävistäjät.
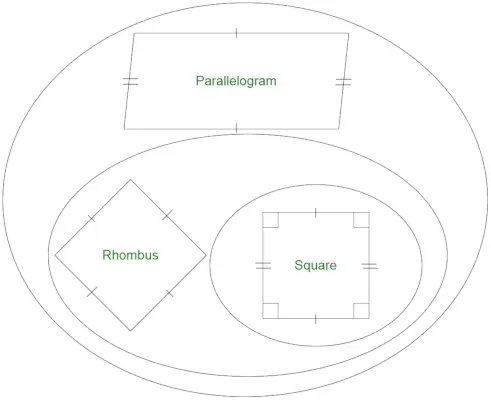
Voimme helposti huomata, että jokainen rombi on suunnikas, mutta päinvastoin ei pidä paikkaansa. Neliötä voidaan pitää rombin erikoistapauksena, koska siinä on neljä yhtä pitkää sivua. Neliössä on kaikki suorat kulmat. Kaikki rombin kulmat eivät kuitenkaan välttämättä ole suoria kulmia . Lopulta rombia, joka sisältää suorat kulmat, voidaan pitää neliönä. Siksi voimme sanoa, että
- Kaikki rombit ovat suuntakuvia.
- Kaikki suunnikkaat eivät ole rombeja.
- Kaikki rombit eivät ole neliöitä.
- Kaikki neliöt ovat rombeja.
Onko jokainen suorakulmio rombi?
Suorakulmio on geometrinen kuvio, joka ei sisällä kaikkia yhtäläisiä puolia. Neliö on erityinen suorakulmio, jonka kaikki sivut ovat yhtä suuret. Koska tiedämme, rombilla on kaikki yhtäläiset sivut. Suorakulmioiden ja rombien joukot leikkaavat vain neliöiden tapauksessa. Siksi suorakulmio ei ole rombi.
missä on kannettavan tietokoneen näppäimistön insert-näppäin

Miksi rombi on suorakulmio?
Rombi on suorakulmion erikoistapaus. Koska tiedämme, että rombin lävistäjät leikkaavat yhtä suuressa kulmassa, kun taas suorakulmion diagonaalit ovat yhtä pitkiä. Kun rombin sivujen keskipisteet yhdistetään, muodostuu suorakulmio.
Lue lisää: Miksi rombi ei ole neliö?
Esimerkkikysymykset – Onko jokainen suorakulmio rombi
Kysymys 1. Laske suorakaiteen muotoisen kehyksen pinta-ala, jonka koko on 6 tuumaa pituus ja 3 tuumaa leveä.
Ratkaisu:
Koska tiedämme,
Suorakulmion pinta-ala = (pituus × leveys) neliöyksikköä.
Korvaamalla arvot, saamme
suorakaiteen muotoisen kehyksen pinta-ala = 6 × 3 = 18 neliötuumaa
Kysymys 2. Etsi sellaisen suorakulmion lävistäjän pituus, jonka pituus on 12 cm ja leveys 8 cm.
Ratkaisu:
Me tiedämme,
Diagonaalin pituus,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Tehtävä 3. Etsi rombin pinta-ala, jonka diagonaali on kaksi pituutta d 1 ja d 2 olla 6 cm ja 12 cm, vastaavasti.
Ratkaisu:
Meillä on,
Diagonaali d1= 6 cm
Diagonaali d2= 12 cm
Rombin pinta-ala saadaan kaavalla,
A =
frac{(d_1 imes d_2)}{2} neliöyksikköäA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Siksi rombin pinta-ala = 36 cm2.
Kysymys 4. Ero rombin ja suorakulmion välillä?
Ratkaisu:
| Omaisuus | Rombi | Suorakulmio |
| Sivut | Tasapuoliset puolet. | Vastakkaiset puolet ovat yhtä suuret. |
| Diagonaalit | Diagonaalit jakavat toisensa 90° kulmassa. Diagonaalit muodostavat suoran kulman keskelle. | Diagonaalit jakavat toisensa eri kulmissa. Toinen kulma on tylppä kulma ja toinen terävä kulma. Diagonaalit muodostavat eri kulmia keskelle – tylpän kulman ja terävän kulman. |
| Kulmat | Vastakkaiset kulmat ovat yhtä suuret. Vierekkäiset kulmat ovat yhteensä 180°. | Vastakkaiset ja vierekkäiset kulmat ovat yhtä suuret. Suorakulmion vierekkäisten sivujen muodostama kulma on 90°. |
