Vähemmän kuin yhtä suuri kuin on epätasa-arvokäsite, joka tarkoittaa, että epäyhtälön vasemmalla puolella oleva termi ei saa olla suurempi kuin oikean puolen termi, eli vasemman termin tulee olla pienempi tai enintään yhtä suuri kuin oikea termi. Artikkeli kattaa käsitteen pienempi tai yhtä suuri matematiikassa, esittelemällä symbolin ≤ ja sen esittämisen numeroviivalla. Se sisältää taulukon matemaattisista symboleista, harjoitustehtävistä ja vastauksia usein kysyttyihin epätasa-arvokysymyksiin.
Sisällysluettelo
mikä on ymail
- Vähemmän kuin merkki
- Pienempi tai yhtä suuri kuin symboli
- Pienempi tai yhtä suuri kuin numerorivillä
- Eriarvoisuuksien symbolimerkinnät
- Vähemmän kuin yhtä suuri ja suurempi kuin yhtä suuri kuin
Vähemmän kuin merkki
Pienempi kuin yhtä suuri merkki on lisätty alla olevaan kuvaan,
Mikä on pienempi tai yhtä suuri kuin?
Pienempi tai yhtä suuri tarkoittaa, että yksi asia ei ole enemmän kuin toinen tai voi olla sama. Esimerkiksi, jos meillä on 2x – 3 ≤ 9, se tarkoittaa, että 2 kertaa luku (x) miinus 3 ei ole suurempi kuin 9. Yksinkertaistaen, jos lisäämme 3 molemmille puolille, saadaan 2x ≤ 12. Sitten jakamalla molemmat puolet 2:lla, löydämme x ≤ 6. Joten se sanoo, että luku (x) voi olla 6 tai pienempi, ja se on silti totta.
Myös Tarkista
- Vähemmän kuin symboli
- Yhtäläisyysmerkki
Vähemmän kuin sama kuin esimerkki
Oletetaan, että Johannes ja Pietari ovat kaksi ystävää ja Johanneksen ikä on pienempi tai yhtä suuri kuin Pietari. Se tarkoittaa, että Johannes on Pietarin ikää nuorempi tai yhtä suuri. Toisin sanoen voimme sanoa, että Pietari on Johanneksen ikää vanhempi tai vähintään yhtä suuri.
Oletetaan nyt, että Johanneksen ikä on x vuotta ja Pietarin 'y' vuotta, niin voimme kirjoittaa tämän yhtälön muodossa seuraavasti:
x ≤ y
missä,
- x on Johanneksen ikä
- y on Pietarin ikä
Pienempi tai yhtä suuri kuin symboli
Symboli pienempi tai yhtä suuri kuin. on ≤
Sitä käytetään matematiikassa kahden suuren vertaamiseen. Tarkemmin sanottuna, kun näet a ≤ b, se tarkoittaa, että a on joko pienempi tai yhtä suuri kuin b. Tämä symboli yhdistää idean alle (<) ja yhtä suuresta (=). Joten se osoittaa, että symbolin vasemmalla puolella oleva arvo on joko pienempi tai sama kuin oikealla puolella oleva arvo. Tämä auttaa ilmaisemaan lukujen tai matemaattisten lausekkeiden välisiä suhteita, joissa yksi voi olla pienempi kuin toinen tai yhtä suuri kuin se.
Pienempi tai yhtä suuri kuin numerorivillä
Käsite pienempi tai yhtä suuri lukurivillä on perustavanlaatuinen matemaattinen lauseke, jota käytetään numeeristen arvojen vertailuun. Tässä yhteydessä se tarkoittaa, että tietty luku on joko pienempi tai yhtä suuri kuin toinen luku. Kun tätä suhdetta esitetään lukusuoralla, pienempi tai yhtä suuren arvon pisteeseen sijoitetaan suljettu ympyrä (●). Esimerkiksi x ≤ 2 esitetään numerorivillä seuraavasti
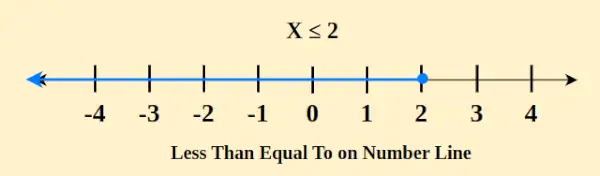
Lisäksi tästä pisteestä oikealle ulottuu viiva, joka kattaa kaikki luvut, jotka ovat suurempia tai yhtä suuria kuin määritetty arvo. Suljetun ympyrän sisällyttäminen korostaa, että päätepiste on osa vertailua. Havainnollistamiseksi, jos A ≤ B, piste A voidaan sijoittaa pisteen B kohdalle tai sen vasemmalle puolelle numeroviivalla, mikä osoittaa, että A on joko pienempi tai yhtä suuri kuin B, mukaan lukien mahdollisuus, että A on yhtä suuri kuin B. Tämä visuaalinen esitys auttaa ymmärtämään vertailuarvojen suhteellisia suuruuksia.
Eriarvoisuuksien symbolimerkinnät
Alla on lisätty erilaiset epäyhtälömerkit ja niiden kuvaukset:
| Epäyhtälöt Symbolimerkintä | |
|---|---|
| Symbolin kuvaus | Symbolimerkintä |
| Suurempi kuin merkki | > |
| Alle merkki | < |
| Sama kuin allekirjoitus | = |
| Ei ole sama kuin merkki | ≠ |
| Suurempi pienempi tai yhtä suuri kuin | ≥ |
| Pienempi kuin tai yhtä suuri kuin | ≤ |
Pienempi kuin yhtä suuri ja suurempi kuin yhtä suuri kuin
Alla mainittu vertailu Suurempi kuin yhtä suuri ja pienempi kuin yhtä suuri kuin:
| Ero suurempi kuin yhtä suuri ja pienempi kuin yhtä suuri kuin | ||
|---|---|---|
| Aspekti | Suurempi kuin yhtä suuri kuin | Vähemmän kuin yhtä suuri kuin |
| Merkitys | Osoittaa arvon, joka on suurempi tai pienin yhtä suuri kuin annettu arvo | Ilmoita arvo, joka on pienempi tai enintään yhtä suuri kuin annettu arvo |
| Symboli | ≥ | ≤ |
| Esimerkki | Ramin ikä on suurempi kuin 10 vuotta ⇒ Ramin ikä ≥ 10 | Rohanin ikä on alle 15 vuotta ⇒ Rohanin ikä ≤ 15 |
Liittyvät lukemat ,
- Suurempi kuin pienempi kuin
- Suurempi kuin tai yhtä suuri kuin
- Epätasa-arvo
Vähemmän kuin yhtä suuri kuin – esimerkkejä
Esimerkki 1. Ratkaise epäyhtälö: 3x – 5 ≤ 10.
Ratkaisu:
Aloita lisäämällä 5 molemmille puolille:
3x ≤ 15
Jaa sitten 3:lla: x ≤ 5
Joten ratkaisu on x ≤ 5
Esimerkki 2. Ratkaise epäyhtälö: -2y + 7 ≤ 1.
Ratkaisu:
Vähennä 7 molemmilta puolilta: -2y ≤ -6
Jaa -2:lla, muista kääntää eriarvoisuusmerkki: y ≥ 3
Ratkaisu on y ≥ 3
xor javassa
Vähemmän kuin yhtä suuri kuin – harjoitusongelmia
Kokeile seuraavia harjoitusongelmia, jotka perustuvat käsitteeseen Vähemmän kuin yhtä suuri
Q1. Ratkaise epäyhtälö: 2y – 8 on pienempi tai yhtä suuri kuin 10.
Q2. Jos m on 6 ja n on 3, määritä, onko m neliö miinus 5 pienempi tai yhtä suuri kuin 2n plus 1.
Q3. Ratkaise x: 3x plus 7 on pienempi tai yhtä suuri kuin 22.
Q4. Jos q on positiivinen luku siten, että 4q miinus 6 on pienempi tai yhtä suuri kuin 14, etsi q:n mahdolliset arvot.
Q5. Määritä a:n arvoalue, joka täyttää epäyhtälön 2a plus 5 on pienempi tai yhtä suuri kuin 15.
Vähemmän kuin yhtä suuri – UKK
1. Mikä on pienempi tai yhtä suuri kuin?
Pienempi tai yhtä suuri kuin tarkoittaa kahden arvon välistä suhdetta, mikä tarkoittaa, että ensimmäinen arvo on joko pienempi tai yhtä suuri kuin toinen.
2. Kuinka Pienempi tai yhtä suuri esitetään lukujonolla?
Numeroviivalla tämä suhde esitetään visuaalisesti asettamalla suljettu ympyrä (●) pienempää tai samansuuruista arvoa vastaavan luvun päälle ja jatkamalla viivaa oikealle, joka kattaa kaikki tätä arvoa suuremmat tai yhtä suuret luvut.
3. Mitä suljettu ympyrä merkitsee numerorivillä?
Suljettu ympyrä korostaa päätepisteen sisällyttämistä vertailuun. Jos esimerkiksi A ≤ B, se osoittaa, että piste A on joko numeroviivan pisteessä B tai sen vasemmalla puolella, mukaan lukien mahdollisuus, että A on yhtä suuri kuin B.
4. Mikä on esimerkki Vähemmän tai yhtä suuren epätasa-arvon ratkaisemisesta?
Tarkastellaan epäyhtälöä 2x – 3 ≤ 9. Jos molemmille puolille lisätään 3, saadaan 2x ≤ 12. Sitten jakamalla molemmat puolet 2:lla saadaan x ≤ 6. Epäyhtälön ratkaisu on siis x ≤ 6.
5. Kuinka ratkaista epätasa-arvo, johon liittyy vähemmän kuin tai yhtä suuri kuin?
Epäyhtälöiden, kuten ax + b ≤ c, ratkaisemiseksi tavallinen lähestymistapa käsittää epäyhtälön manipuloimisen yhteen-, vähennys-, kerto- tai jakolaskulla, jolloin muuttuja eristetään ja epäyhtälöä tyydyttävä arvoalue määritetään.
6. Mikä on pienempi kuin yhtä suuri ja suurempi kuin yhtä suuri symboli?
Symboli Vähemmän kuin yhtä suuri kuin on ≤ kun taas symboli suurempi kuin yhtä suuri on ≥.
