Kun annetaan kaksi merkkijonoa, S1 ja S2 , tehtävänä on löytää pisimmän yhteisen osajonon pituus, eli pisin molemmissa merkkijonoissa esiintyvä osasekvenssi.

A pisin yhteinen osasekvenssi (LCS) määritellään pisimmäksi osasekvenssiksi, joka on yhteinen kaikissa annetuissa syöttösekvensseissä.

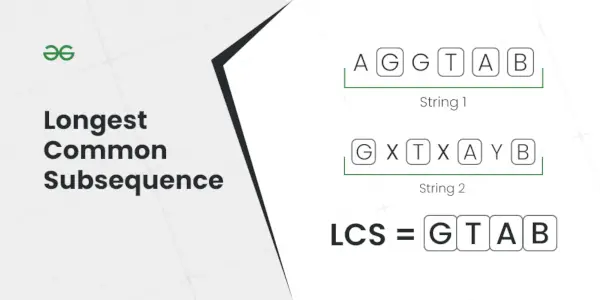
Pisin yhteinen jakso

rohit shetty näyttelijä

Esimerkkejä:

Syöte: S1 = ABC, S2 = ACD
Lähtö: 2
Selitys: Pisin molemmissa merkkijonoissa esiintyvä osasekvenssi on AC.

Syöte: S1 = AGGTAB, S2 = GXTXAYB
Lähtö: 4
Selitys: Pisin yhteinen osasekvenssi on GTAB.

Syöte: S1 = ABC, S2 = CBA
Lähtö: 1
Selitys: On olemassa kolme yhteistä osasekvenssiä, joiden pituus on 1, A, B ja C, eikä mitään yhteistä osasekvenssiä, joiden pituus on yli 1.

Syöte: S1 = XYZW, S2 = XYWZ
Lähtö: 3
Selitys: On olemassa kaksi yhteistä osasekvenssiä, joiden pituus on 3 XYZ ja XYW, eikä yhteistä osasekvenssiä. pituus yli 3.

Pisin yhteinen osasekvenssi (LCS) rekursiolla:

Luo kaikki mahdolliset osasekvenssit ja etsi niistä pisin, joka on läsnä molemmissa merkkijonoissa käyttämällä Toteuta idea noudattamalla seuraavia ohjeita:

• Luo rekursiivinen funktio [sano lcs() ].
• Tarkista vielä käsittelemättömien merkkijonojen ensimmäisten merkkien välinen suhde.
  • Suhteesta riippuen kutsu seuraava rekursiivinen funktio edellä mainitulla tavalla.
• Palauta vastauksena saadun LCS:n pituus.

Alla on rekursiivisen lähestymistavan toteutus:

C++

// A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

C

// A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b)? a: b; } // Ohjainkoodi int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0, j = 0;  // Toimintokutsu printf('LCS:n pituus on %d', lcs(S1, S2, i, j));  paluu 0; }>

Java

// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b)? a: b; } // Ohjainkoodi public static void main(String[] args) { Pisin yhteinenSubsequence lcs = new LongestCommonSubsequence();  Merkkijono S1 = 'AGGTAB';  Merkkijono S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('LCS:n pituus on' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Tämän koodin tarjoaa Saket Kumar>>Python

C#

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b)? a: b; } // Ohjainkoodi public static void Main() { String S1 = 'AGGTAB';  Merkkijono S2 = 'GXTXAYB';  int m = S1.Pituus;  int n = S2.Pituus;  Console.Write('LCS:n pituus on' + ' ' + lcs(S1, S2, m, n));  } } // Tämän koodin tarjoaa Sam007>>Javascript>>PHP>>  
  Lähtö  
Length of LCS is 4>
  
    Aika monimutkaisuus:    O(2m+n)  
    Aputila:    O(1)
 
Pisin yhteinen subsequence (LCS) käyttää  Memoisointi : 
 Jos huomaamme huolellisesti, voimme havaita, että yllä olevalla rekursiivisella ratkaisulla on seuraavat kaksi ominaisuutta: 
  
1. Optimaalinen alusrakenne:
Katso L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) rakenteen ratkaisemiseen otamme avuksi X[0:n alirakenteet , 1, …, m-2], Y[0, 1,…, n-2] tilanteesta riippuen (eli käyttämällä niitä optimaalisesti) kokonaisuuden ratkaisun löytämiseksi.
 
2. Päällekkäiset aliongelmat:
Jos käytämme yllä olevaa rekursiivista lähestymistapaa merkkijonoihin    BD    ja    ABCD    , saamme osittaisen rekursiopuun alla olevan kuvan mukaisesti. Tästä nähdään, että aliongelmaa L(BD, ABCD) lasketaan useammin kuin kerran. Jos koko puu otetaan huomioon, tällaisia ​​päällekkäisiä aliongelmia on useita.
  
L(AXYT, AYZX)  
/  
L(AXY, AYZX) L(AXYT, AYZ)  
/  /   
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)
 
    Lähestyä:    Näiden kahden ominaisuuden vuoksi voimme käyttää dynaamista ohjelmointia tai muistiinpanoa ongelman ratkaisemiseen. Alla on lähestymistapa ratkaisuun, jossa käytetään rekursiota.
  
Luo rekursiivinen funktio. Luo myös 2D-taulukko tallentaaksesi ainutlaatuisen tilan tuloksen.
Jos samaa tilaa kutsutaan rekursiokutsun aikana useammin kuin kerran, voimme suoraan palauttaa tälle tilalle tallennetun vastauksen uudelleen laskemisen sijaan.
Alla on yllä olevan lähestymistavan toteutus:
C++ 
// A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) palauttaa 0;  jos (X[m - 1] == Y[n - 1]) palauttaa dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } paluu dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Ohjainkoodi int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  vektori> dp(m + 1, vektori (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>
 Java 
/*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>
 Python 
# A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>
 C# 
/* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>b)? a: b; } public static void Main() { String s1 = 'AGGTAB';  Merkkijono s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X. pituus;  int n = Y.Pituus;  int[, ] L = uusi int[m + 1, n + 1];  for (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>
 Javascript 
/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>
   
  Lähtö      Aika monimutkaisuus:    O(m * n) missä m ja n ovat merkkijonon pituudet.  
    Aputila:    O(m * n) Tässä rekursiivinen pinotila jätetään huomioimatta.
 
Pisin yhteinen osasekvenssi (LCS) alhaalta ylös (taulukko):
Voimme käyttää seuraavia vaiheita toteuttaaksemme LCS:n dynaamisen ohjelmointitavan.
 
Luo 2D-taulukko    dp[][]    jossa rivit ja sarakkeet ovat yhtä pitkiä kuin kunkin syötemerkkijonon pituus plus 1 [rivien lukumäärä ilmaisee    S1    ja sarakkeet osoittavat indeksit    S2    ].
Alusta dp-taulukon ensimmäinen rivi ja sarake 0:ksi.
Iteroi dp-taulukon rivien läpi alkaen 1:stä (sanotaan käyttämällä iteraattoria    i    ).
Jokaiselle    i    , iteroi kaikki sarakkeet kohteesta    j = 1 - n    :
Jos    S1[i-1]    on yhtä suuri kuin    S2[j-1]    , aseta dp-taulukon nykyinen elementti elementin arvoksi (    dp[i-1][j-1] + 1    ).
Muussa tapauksessa aseta dp-taulukon nykyinen elementti maksimiarvoon    dp[i-1][j]    ja    dp[i][j-1]    .
Sisäkkäisten silmukoiden jälkeen dp-taulukon viimeinen elementti sisältää LCS:n pituuden.
Katso alla oleva kuva ymmärtääksesi paremmin:
 
    Kuva:    
verkon topologia
  
Sano, että jouset ovat    S1 = AGGTAB    ja    S2 = GXTXAYB    .
 
    Ensimmäinen askel:    Luo aluksi 2D-matriisi (esimerkiksi dp[][]), jonka koko on 8 x 7 ja jonka ensimmäinen rivi ja ensimmäinen sarake on täytetty 0:lla.
  
dp-taulukon luominen
    Toinen vaihe:    Kulje i = 1. Kun j:stä tulee 5, S1[0] ja S2[4] ovat yhtä suuret. Joten dp[][] päivitetään. Muille elementeille otetaan maksimiarvot dp[i-1][j] ja dp[i][j-1]. (Tässä tapauksessa, jos molemmat arvot ovat samat, olemme käyttäneet nuolia edellisille riveille).
  
Täytä rivi nro 1
    Kolmas vaihe:    Vaikka kuljetaan arvolla i = 2, S1[1] ja S2[0] ovat samat (molemmat ovat 'G'). Joten dp-arvo kyseisessä solussa päivitetään. Loput elementit päivitetään ehtojen mukaisesti.
  
Täytetään rivi nro. 2
    Neljäs vaihe:    Jos i = 3, S1[2] ja S2[0] ovat jälleen samat. Päivitykset ovat seuraavat.
  
Täyttörivi nro. 3
    Viides vaihe:    Jos i = 4, voimme nähdä, että S1[3] ja S2[2] ovat samat. Joten dp[4][3] päivitetty muodossa dp[3][2] + 1 = 2.
  
Täytä rivi 4
    Kuudes vaihe:    Tästä voimme nähdä, että i = 5 ja j = 5 arvot S1[4] ja S2[4] ovat samat (eli molemmat ovat 'A'). Joten dp[5][5] päivitetään vastaavasti ja siitä tulee 3.
  
Täytä rivi 5
    Viimeinen vaihe:    Jos i = 6, katso, että molempien merkkijonojen viimeiset merkit ovat samat (ne ovat 'B'). Siksi dp[6][7]:n arvoksi tulee 4.
  
Viimeisen rivin täyttäminen
Joten saamme yhteisen osasekvenssin enimmäispituuden as    4    .
 
Seuraavassa on taulukkomuotoinen toteutus LCS-ongelmalle.
C++ 
// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>
 Java 
// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b)? a: b; } public staattinen void main(String[] args) { Pisin yhteinenSubsequence lcs = new PisinYleinenSubsequence();  Merkkijono S1 = 'AGGTAB';  Merkkijono S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('LCS:n pituus on' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Tämän koodin tarjoaa Saket Kumar>
 Python 
# Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>
 C# 
// Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b)? a: b; } // Ohjainkoodi public static void Main() { String S1 = 'AGGTAB';  Merkkijono S2 = 'GXTXAYB';  int m = S1.Pituus;  int n = S2.Pituus;  Console.Write('LCS:n pituus on' + ' ' + lcs(S1, S2, m, n));  } } // Tämän koodin tarjoaa Sam007>>Javascript
 PHP 
 // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>>  
  Lähtö  
Length of LCS is 4>
  
    Aika monimutkaisuus:    O(m * n), joka on paljon parempi kuin Naive Recursive -toteutuksen pahimman mahdollisen aikamonimutkaisuus.  
    Aputila:    O(m * n), koska algoritmi käyttää taulukkoa, jonka koko on (m+1)*(n+1), tallentaakseen yhteisten osamerkkijonojen pituuden.
 
Pisin yhteinen osasekvenssi (LCS) alhaalta ylöspäin (tilan optimointi):
 
Yllä olevassa taulukkomenetelmässä käytämme L[i-1][j] ja L[i][j] jne, tässä L[i-1] viittaa matriisin L edelliseen riviin ja L[i] viittaa nykyinen rivi.
Tilan optimointi voidaan tehdä käyttämällä kahta vektoria, joista toinen on edellinen ja toinen nykyinen.
Kun sisäinen for-silmukka poistuu, alustamme edellisen yhtä suureksi kuin nykyinen.
Alla toteutus:
C++ 
// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector ed. (m + 1, 0), cur (m + 1, 0);  for (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>
 Java 
// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>
 Python 
def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>
 C# 
using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>
 Javascript 
function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>
   
  Lähtö      Aika monimutkaisuus:    O(m * n), joka pysyy samana.  
    Aputila:    O(m), koska algoritmi käyttää kahta taulukkoa, joiden koko on m.
lausunnon tulostaminen javassa