Kun on annettu kaksi merkkijonoa 'X' ja 'Y', etsi pisimmän yhteisen osamerkkijonon pituus.
Esimerkkejä:
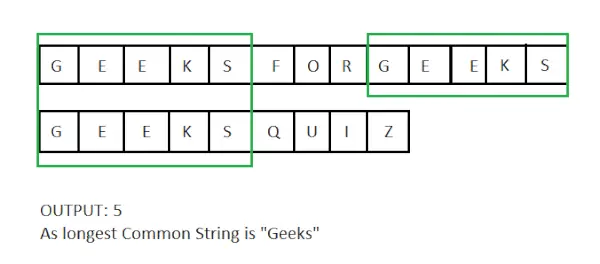
Syöte: X = techcodeview.com, y = GeeksQuiz
Lähtö : 5
Selitys:
Pisin yleinen osamerkkijono on Geeks ja sen pituus on 5.
Syöte: X = abcdxyz, y = xyzabcd
Lähtö: 4
Selitys:
Pisin yhteinen osamerkkijono on abcd ja sen pituus on 4.Syöte: X = zxabcdezy, y = yzabcdezx
Lähtö: 6
Selitys:
Pisin yhteinen osamerkkijono on abcdez ja sen pituus on 6.
Lähestyä:
Olkoot m ja n vastaavasti ensimmäisen ja toisen merkkijonon pituudet.
A yksinkertainen ratkaisu on yksitellen harkita ensimmäisen merkkijonon kaikkia osamerkkijonoja ja jokaisen osamerkkijonon kohdalla tarkista, onko se toisen merkkijonon osamerkkijono. Seuraa enimmäispituutta alimerkkijonoa. Siellä tulee olemaan O(m^2) alimerkkijonoa ja voimme selvittää, onko merkkijono toisessa merkkijonossa O(n) ajassa (katso Tämä ). Joten tämän menetelmän kokonaisaika monimutkaisuus olisi O(n * m2)
Dynaaminen ohjelmointi voidaan käyttää pisimmän yhteisen osajonon löytämiseen O(m*n) ajassa. Ajatuksena on löytää pisimmän yhteisen päätteen pituus molempien merkkijonojen kaikille alijonoille ja tallentaa nämä pituudet taulukkoon.
Pisimmällä yleisellä liitteellä on seuraava optimaalinen alirakenneominaisuus.
Jos viimeiset merkit täsmäävät, vähennämme molempia pituuksia yhdellä
- LCSuff(X, Y, m, n) = LCSuff(X, Y, m-1, n-1) + 1, jos X[m-1] = Y[n-1]
Jos viimeiset merkit eivät täsmää, tulos on 0, ts.
- LCSuff(X, Y, m, n) = 0 jos (X[m-1] != Y[n-1])
Nyt tarkastellaan eri alimerkkijonojen päätteitä, jotka päättyvät eri indekseihin.
Suurin pituus Pisin yhteinen pääte on pisin yhteinen osamerkkijono.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)) missä 1 <= i <= m ja 1 <= j <= n
Seuraavassa on yllä olevan ratkaisun iteratiivinen toteutus.
C++
/* Dynamic Programming solution to> >find length of the> >longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> >common substring of X[0..m-1]> >and Y[0..n-1] */> int> LCSubStr(>char>* X,>char>* Y,>int> m,>int> n)> {> >// Create a table to store> >// lengths of longest> >// common suffixes of substrings.> >// Note that LCSuff[i][j] contains> >// length of longest common suffix> >// of X[0..i-1] and Y[0..j-1].> >int> LCSuff[m + 1][n + 1];> >int> result = 0;>// To store length of the> >// longest common substring> >/* Following steps build LCSuff[m+1][n+1] in> >bottom up fashion. */> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >// The first row and first column> >// entries have no logical meaning,> >// they are used only for simplicity> >// of program> >if> (i == 0 || j == 0)> >LCSuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> >result = max(result, LCSuff[i][j]);> >}> >else> >LCSuff[i][j] = 0;> >}> >}> >return> result;> }> // Driver code> int> main()> {> >char> X[] =>'OldSite:techcodeview.com.org'>;> >char> Y[] =>'NewSite:GeeksQuiz.com'>;> >int> m =>strlen>(X);> >int> n =>strlen>(Y);> >cout <<>'Length of Longest Common Substring is '> ><< LCSubStr(X, Y, m, n);> >return> 0;> }> |
>
>
Java
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> >/*> >Returns length of longest common substring> >of X[0..m-1] and Y[0..n-1]> >*/> >static> int> LCSubStr(>char> X[],>char> Y[],>int> m,>int> n)> >{> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> >int> LCStuff[][] =>new> int>[m +>1>][n +>1>];> >// To store length of the longest> >// common substring> >int> result =>0>;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (>int> i =>0>; i <= m; i++) {> >for> (>int> j =>0>; j <= n; j++) {> >if> (i ==>0> || j ==>0>)> >LCStuff[i][j] =>0>;> >else> if> (X[i ->1>] == Y[j ->1>]) {> >LCStuff[i][j]> >= LCStuff[i ->1>][j ->1>] +>1>;> >result = Integer.max(result,> >LCStuff[i][j]);> >}> >else> >LCStuff[i][j] =>0>;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> main(String[] args)> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.length();> >int> n = Y.length();> >System.out.println(> >'Length of Longest Common Substring is '> >+ LCSubStr(X.toCharArray(), Y.toCharArray(), m,> >n));> >}> }> // This code is contributed by Sumit Ghosh> |
>
>
Python 3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> ># Create a table to store lengths of> ># longest common suffixes of substrings.> ># Note that LCSuff[i][j] contains the> ># length of longest common suffix of> ># X[0...i-1] and Y[0...j-1]. The first> ># row and first column entries have no> ># logical meaning, they are used only> ># for simplicity of the program.> ># LCSuff is the table with zero> ># value initially in each cell> >LCSuff>=> [[>0> for> k>in> range>(n>+>1>)]>for> l>in> range>(m>+>1>)]> ># To store the length of> ># longest common substring> >result>=> 0> ># Following steps to build> ># LCSuff[m+1][n+1] in bottom up fashion> >for> i>in> range>(m>+> 1>):> >for> j>in> range>(n>+> 1>):> >if> (i>=>=> 0> or> j>=>=> 0>):> >LCSuff[i][j]>=> 0> >elif> (X[i>->1>]>=>=> Y[j>->1>]):> >LCSuff[i][j]>=> LCSuff[i>->1>][j>->1>]>+> 1> >result>=> max>(result, LCSuff[i][j])> >else>:> >LCSuff[i][j]>=> 0> >return> result> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> print>(>'Length of Longest Common Substring is'>,> >LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
>
>
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> >// Returns length of longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> LCSubStr(>string> X,>string> Y,>int> m,>int> n)> >{> >// Create a table to store lengths of> >// longest common suffixes of substrings.> >// Note that LCSuff[i][j] contains length> >// of longest common suffix of X[0..i-1]> >// and Y[0..j-1]. The first row and first> >// column entries have no logical meaning,> >// they are used only for simplicity of> >// program> >int>[, ] LCStuff =>new> int>[m + 1, n + 1];> >// To store length of the longest common> >// substring> >int> result = 0;> >// Following steps build LCSuff[m+1][n+1]> >// in bottom up fashion> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >if> (i == 0 || j == 0)> >LCStuff[i, j] = 0;> >else> if> (X[i - 1] == Y[j - 1])> >{> >LCStuff[i, j]> >= LCStuff[i - 1, j - 1] + 1;> >result> >= Math.Max(result, LCStuff[i, j]);> >}> >else> >LCStuff[i, j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> Main()> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >Console.Write(>'Length of Longest Common'> >+>' Substring is '> >+ LCSubStr(X, Y, m, n));> >}> }> // This code is contributed by Sam007.> |
>
>
Javascript
java lajittelutaulukko
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> >/*> >Returns length of longest common> >substring of X[0..m-1] and Y[0..n-1]> >*/> >function> LCSubStr( X, Y , m , n) {> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> > >var> LCStuff => >Array(m + 1).fill().map(()=>Array(n + 1).fill(0));> >// To store length of the longest> >// common substring> >var> result = 0;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (i = 0; i <= m; i++) {> >for> (j = 0; j <= n; j++) {> >if> (i == 0 || j == 0)> >LCStuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> >result = Math.max(result, LCStuff[i][j]);> >}>else> >LCStuff[i][j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> > >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> >var> m = X.length;> >var> n = Y.length;> >document.write(>'Length of Longest Common Substring is '> +> >LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
>
>
PHP
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>>> |
>Length of Longest Common Substring is 10>
Aika monimutkaisuus: O(m*n)
Aputila: O(m*n), koska m*n lisätilaa on otettu.
Toinen lähestymistapa: (Avaruusoptimoitu lähestymistapa).
Yllä olevassa lähestymistavassa käytämme vain 2D-taulukon viimeistä riviä, joten voimme optimoida tilan käyttämällä
2-D-taulukko, jonka mitat ovat 2*(min(n,m)).
Alla on yllä olevan lähestymistavan toteutus:
C++
#include> #include> using> namespace> std;> // Function to find the length of the longest LCS> int> LCSubStr(string s, string t,>int> n,>int> m)> {> >// Create DP table> >vectorint>> dp(n + 1, vektori |
>
>
Java
// Java implementation of the above approach> import> java.io.*;> class> GFG> {> > >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(String s,String t,> >int> n,>int> m)> >{> > >// Create DP table> >int> dp[][]=>new> int>[>2>][m+>1>];> >int> res=>0>;> > >for>(>int> i=>1>;i<=n;i++)> >{> >for>(>int> j=>1>;j<=m;j++)> >{> >if>(s.charAt(i->1>)==t.charAt(j->1>))> >{> >dp[i%>2>][j]=dp[(i->1>)%>2>][j->1>]+>1>;> >if>(dp[i%>2>][j]>res)> >res=dp[i%>2>][j];> >}> >else> dp[i%>2>][j]=>0>;> >}> >}> >return> res;> >}> > >// Driver Code> >public> static> void> main (String[] args)> >{> >String X=>'OldSite:techcodeview.com.org'>;> >String Y=>'NewSite:GeeksQuiz.com'>;> > >int> m=X.length();> >int> n=Y.length();> > >// Function call> >System.out.println(LCSubStr(X,Y,m,n));> > >}> }> |
>
>
Python 3
# Python implementation of the above approach> # Function to find the length of the> # longest LCS> def> LCSubStr(s, t, n, m):> > ># Create DP table> >dp>=> [[>0> for> i>in> range>(m>+> 1>)]>for> j>in> range>(>2>)]> >res>=> 0> > >for> i>in> range>(>1>,n>+> 1>):> >for> j>in> range>(>1>,m>+> 1>):> >if>(s[i>-> 1>]>=>=> t[j>-> 1>]):> >dp[i>%> 2>][j]>=> dp[(i>-> 1>)>%> 2>][j>-> 1>]>+> 1> >if>(dp[i>%> 2>][j]>res):> >res>=> dp[i>%> 2>][j]> >else>:> >dp[i>%> 2>][j]>=> 0> >return> res> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> # Function call> print>(LCSubStr(X,Y,m,n))> # This code is contributed by avanitrachhadiya2155> |
>
>
C#
// C# implementation of the above approach> using> System;> public> class> GFG> {> >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(>string> s,>string> t,> >int> n,>int> m)> >{> >// Create DP table> >int>[,] dp =>new> int>[2, m + 1];> >int> res = 0;> >for>(>int> i = 1; i <= n; i++)> >{> >for>(>int> j = 1; j <= m; j++)> >{> >if>(s[i - 1] == t[j - 1])> >{> >dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;> >if>(dp[i % 2, j]>res)> >res = dp[i % 2, j];> >}> >else> dp[i % 2, j] = 0;> >}> >}> >return> res;> >}> >// Driver Code> >static> public> void> Main (){> >string> X =>'OldSite:techcodeview.com.org'>;> >string> Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >// Function call> >Console.WriteLine(LCSubStr(X,Y,m,n));> >}> }> // This code is contributed by rag2127> |
>
>
Javascript
> // JavaScript implementation of the above approach> >// Function to find the length of the> >// longest LCS> >function> LCSubStr(s, t, n, m)> >{> > >// Create DP table> >var> dp = Array(2).fill().map(()=>Taulukko(m+1).täytä(0));> >var> res = 0;> > >for>(>var> i = 1; i <= n; i++)> >{> >for>(>var> j = 1; j <= m; j++)> >{> >if>(s.charAt(i - 1) == t.charAt(j - 1))> >{> >dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;> >if>(dp[i % 2][j]>res)> >res = dp[i % 2][j];> >}> >else> dp[i % 2][j] = 0;> >}> >}> >return> res;> >}> > >// Driver Code> >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> > >var> m = X.length;> >var> n = Y.length;> > >// Function call> >document.write(LCSubStr(X, Y, m, n));> // This code is contributed by shivanisinghss2110> > |
>
>Lähtö
10>
Aika monimutkaisuus: O(n*m)
Aputila: O(min(m,n))
Toinen lähestymistapa: (Käytetään rekursiota)
Tässä on yllä olevan lähestymistavan rekursiivinen ratkaisu.
C++
// C++ program using to find length of the> // longest common substring recursion> #include> using> namespace> std;> string X, Y;> // Returns length of function f> // or longest common substring> // of X[0..m-1] and Y[0..n-1]> int> lcs(>int> i,>int> j,>int> count)> {> >if> (i == 0 || j == 0)> >return> count;> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = max(count,> >max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> }> // Driver code> int> main()> {> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.size();> >m = Y.size();> >cout << lcs(n, m, 0);> >return> 0;> }> |
>
>
Java
// Java program using to find length of the> // longest common substring recursion> import> java.io.*;> class> GFG {> >static> String X, Y;> >// Returns length of function> >// for longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i ==>0> || j ==>0>)> >{> >return> count;> >}> >if> (X.charAt(i ->1>)> >== Y.charAt(j ->1>))> >{> >count = lcs(i ->1>, j ->1>, count +>1>);> >}> >count = Math.max(count,> >Math.max(lcs(i, j ->1>,>0>),> >lcs(i ->1>, j,>0>)));> >return> count;> >}> > >// Driver code> >public> static> void> main(String[] args)> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.length();> >m = Y.length();> >System.out.println(lcs(n, m,>0>));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Python 3
# Python3 program using to find length of> # the longest common substring recursion> # Returns length of function for longest> # common substring of X[0..m-1] and Y[0..n-1]> def> lcs(i, j, count):> >if> (i>=>=> 0> or> j>=>=> 0>):> >return> count> >if> (X[i>-> 1>]>=>=> Y[j>-> 1>]):> >count>=> lcs(i>-> 1>, j>-> 1>, count>+> 1>)> >count>=> max>(count,>max>(lcs(i, j>-> 1>,>0>),> >lcs(i>-> 1>, j,>0>)))> >return> count> # Driver code> if> __name__>=>=> '__main__'>:> >X>=> 'abcdxyz'> >Y>=> 'xyzabcd'> >n>=> len>(X)> >m>=> len>(Y)> >print>(lcs(n, m,>0>))> # This code is contributed by Ryuga> |
>
>
C#
// C# program using to find length> // of the longest common substring> // recursion> using> System;> class> GFG {> >static> String X, Y;> >// Returns length of function for> >// longest common substring of> >// X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i == 0 || j == 0) {> >return> count;> >}> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> >// Driver code> >public> static> void> Main()> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.Length;> >m = Y.Length;> >Console.Write(lcs(n, m, 0));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Javascript
> >// Javascript program using to find length of the> >// longest common substring recursion> >let X, Y;> > >// Returns length of function f> >// or longest common substring> >// of X[0..m-1] and Y[0..n-1]> >function> lcs(i, j, count)> >{> > >if> (i == 0 || j == 0)> >return> count;> > >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.max(count,> >Math.max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> > >let n, m;> > >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> > >n = X.length;> >m = Y.length;> > >document.write(lcs(n, m, 0));> > >// This code is contributed by divyeshrabadiya07.> > |
>
>
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>>> |
>4>
Aika monimutkaisuus : O(2^max(m,n)) koska funktio tekee kaksi rekursiivista kutsua – lcs(i, j-1, 0) ja lcs(i-1, j, 0), kun merkit kohdassa X[i-1] != Y[j-1]. Joten se antaa pahimman tapauksen aikakompleksisuuden muodossa 2^N, missä N = max(m, n), m ja n on X- ja Y-merkkijonon pituus.
Aputila: O(1): koska funktiokutsu ei käytä ylimääräistä tilaa (funktio käyttää vain rekursiivista kutsupinoa, jota emme yleensä ota huomioon aputilassa).
