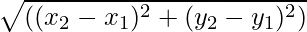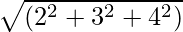logo

TechCodeview

Vektorin suuruus

Vektorisuureet ovat suureita, joilla on sekä suunta että suuruus. Vektorin suuruus on vektorin pituus. Se annetaan vektorin numeerisella arvolla ja koska se edustaa vektorin pituutta, niin se on aina positiivinen. Mille tahansa vektorille 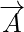overrightarrow{A}sen suuruus on esitetty muodossa overrightarrow{A}.

Otetaan lisätietoja vektorin suuruudesta sen kaavasta, esimerkeistä ja muista tässä artikkelissa.



Sisällysluettelo

Mikä on vektorin suuruus?

Vektorin suuruus määritellään vektorin pituudeksi. Koska vektorin suuruus ilmaisee vektorin pituuden, se on aina positiivinen. Minkä tahansa vektorin A suuruus esitetään muodossa |A|. Oletetaan, että vektori määritellään muodossa xi + yj, niin sen suuruus määritellään yksittäisten termien neliösumman neliöjuureksi. Vektorin suuruus edustaa vektorin pituutta eli vektorin arvoa tai vaikutusta.

Esimerkiksi, jos 5i N:n voima vaikuttaa kohteeseen, sen suuruus on 5 N, mikä tarkoittaa, että käytetyn voiman voimakkuus on 5 N, ja ' minä' 5i tarkoittaa, että sitä sovelletaan positiiviseen x-suunnassa.



Vektorikaavan suuruus

On olemassa erilaisia ​​tapoja laskea vektorin suuruus. Käytä annettujen tietojen perusteella toisenlaista kaavaa vektorin suuruuden selvittämiseen. Vektorin A suuruus esitetään moduulioperaattorilla eli |A|

On olemassa erilaisia ​​​​kaavoja, joita käytetään vektorin suuruuden laskemiseen. Seuraava kuva näyttää tärkeät kaavat, joita käytetään vektorin suuruuden määrittämiseen.

Vektorikaavan suuruus

Seuraavassa on tapoja laskea suuruus.



  • Jos niille annetaan vektori Ā = xi+ yĵ + zk̂, niin vektorin Ā suuruus voidaan laskea alla olevan kaavan avulla

Vektorin  suuruus (|A|) = √(x 2 + ja 2 +z 2 )

  • Jos aloituspistevektori on sano (x1, ja1) ja vektorin päätepiste on sano (x2, ja2) annetaan sitten vektorin suuruus overrightarrow{AB}antaa,
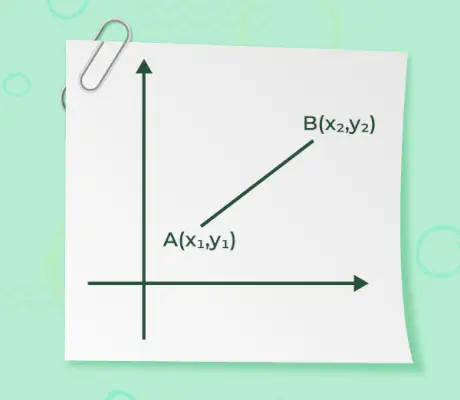
Vektorin suuruus, jos annetaan kaksi pistettä

Vektorin suuruus, kun vektorin alku- ja loppupiste on annettu, ei ole muuta kuin pisteiden välinen etäisyys. Suuruuden löytämisen kaava on annettu kaavalla

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Jos jokin vektorin alku- tai loppupisteistä on origossa o(0, 0) ja toinen piste on A(x, y) kuten alla olevassa kuvassa on määritelty,
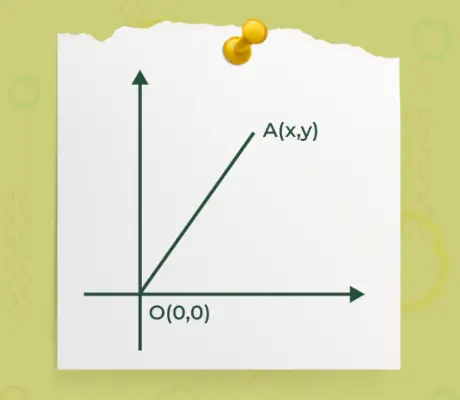
Vektorin magnitudi, jos annetaan yksi piste ja origo

Sitten kaava sellaisen vektorin suuruuden löytämiseksi, jossa vektorin yksi päistä on origossa, on annettu kaavalla

|Ā| = √(x 2 +y 2 )

Vektorin suunta

Vektorisuureet ovat suureita, joilla on sekä suuruus että suunnat. Vektorisuureen suunta ilmaisee, mihin suuntaan vektorisuuretta käytetään. Se määritellään kulmaksi, jonka vektori muodostaa vaakaviivan tai x-akselin kanssa. Sitä edustaa symboli a .

Alla olevassa kuvassa näkyy nuoli, jota käytetään osoittamaan vektorin suunta.

Vektorin suunta

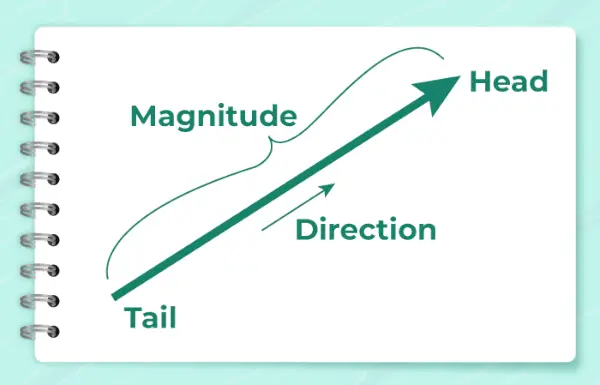
Se lasketaan kaavalla,

α = rusketus -1 (y/x)

linux joka

Koordinaattien generoimalle vektorille (x1, ja1) ja (x2, ja2) niiden suunta on annettu kaavalla,

α = rusketus -1 [(ja 2 - ja 1 )/(x 2 – x 1 )]

Kuinka löytää vektorin suuruus?

Vektorin suuruus lasketaan alla kuvattujen vaiheiden avulla,

Vaihe 1: Tunnista vektorin x-, y- ja z-komponentit.

Vaihe 2 : Etsi kaikkien x-, y- ja z-komponenttien neliö.

Vaihe 3: Lisää kaikki vaiheessa 2 löytyneet neliöt.

Vaihe 4: Etsi vaiheessa 3 saadun summan neliöjuuri.

Vaiheen 4 jälkeen saatu arvo on annetun vektorin suuruus.

Esimerkki: Etsi vektorin A = 3i + 4j magnitudi

Ratkaisu:

Vektorin A suuruus lasketaan käyttämällä edellä käsiteltyjä vaiheita.

Vaihe 1: Vertaamalla A = 3i + 4j ja xi + yj saadaan x = 3 ja y = 4

Vaihe 2: x2= 32= 9 ja y2= 42= 16

muotoinen java-merkkijono

Vaihe 3: x2+ ja2= 9 + 16 = 25

Vaihe 4: √(25) = 5

Siten vektorin A = 3i + 4j magnitudi on 5 yksikköä.

Johtopäätös

Lopuksi vektorin suuruus kertoo, kuinka pitkä vektori on. Tämä käsite on erittäin tärkeä monilla aloilla, kuten fysiikassa, tekniikassa ja tietojenkäsittelytieteessä, koska se auttaa mittaamaan asioita, kuten nopeutta, voimaa ja liikkeen suuntaa. Ymmärtämällä vektorin suuruuden voimme paremmin analysoida ja ratkaista käytännön ongelmia, mikä tekee siitä avaintietoa kaikille, jotka työskentelevät numeroiden ja mittausten kanssa tosielämän sovelluksissa.

Lue lisää,

Ratkaistiin esimerkkejä vektorin suuruudesta

Esimerkki 1: Etsi vektorin Ā = 2i + 3ĵ + 4k suuruus.

Ratkaisu:

satunnainen ei generaattoria javassa

Annettu,

Ā = 2i + 3ĵ + 4k

Suuruus |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Vektorin suuruus 2i+3ĵ+4k On 5.38 yksikkö

Esimerkki 2: Etsi vektorin Ā = 3i + 3ĵ – 6k suuruus

Ratkaisu:

Annettu

Ā = 3i + 3ĵ – 6k

Suuruus |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Vektorin suuruus 3i+ 3ĵ – 6k On 7.35 yksikkö.

Esimerkki 3: Etsi vektorin suuruus, jos vektorin aloituspiste on (3, 4) ja loppupiste on (6, 2).

Ratkaisu:

Annettu,

(x1, ja1) = (3, 4)
(x2, ja2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

ddl vs dml

Siten annetun vektorin suuruus on 3.6 yksikkö.

Esimerkki 4: Selvitä vektorin suuruus, jos vektorin aloituspiste on (2, 1, 4) ja loppupiste on (5, 2, 6).

Ratkaisu:

Annettu,

(x1, ja1, Kanssa1) = (2, 1, 4)

(x2, ja2, Kanssa2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Siten annetun vektorin suuruus on 3.74 yksikkö.

Esimerkki 5: Mikä on vektorin suuruus, joka alkaa origosta ja päätepisteestä kohdasta (3, 4).

Ratkaisu:

Annettu,

Vektorin aloituspiste on O(0, 0)

Päätepiste (x, y) = (3, 4)

Vektorin suuruus (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Siten annetun vektorin suuruus on 5 yksikkö.

Esimerkki 6: Etsi sen vektorin suuruus, jossa yksi päätepisteistä on origossa ja toinen piste kohdassa (1, 4, 3).

Ratkaisu:

Annettu,

Vektorin loppupiste on O(0, 0)

Muu piste (x, y, z) = (1, 4, 3)

Vektorin suuruus (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Siten annetun vektorin suuruus on 5.09 yksikkö.

päivämäärien erot excelissä

Usein kysytyt kysymykset vektorin suuruudesta

Mikä on vektorikaavan suuruus?

Vektorin suuruus on vektorin numeerinen arvo ja se määrittää vektorin pituuden. Minkä tahansa vektorin A suuruus esitetään muodossa |A|. Vektorin suuruus lasketaan kaavalla,

Minkä tahansa vektorin A = xi + yj + zk sen suuruus saadaan kaavalla

|A| = √(x 2 + ja 2 + z 2 )

Jokaiselle vektorille, jonka aloituspiste ja loppupiste ovat vastaavasti (x1, ja1) ja (x2, ja2) sen suuruus saadaan kaavalla

|A| = √((x 2 – x 1 ) 2 + (ja 2 - ja 1 ) 2 )

Kuinka edustaa vektorin suuruutta?

Vektorin suuruus A on merkitty symbolilla |A|.

Kuinka löytää vektorin suuruus?

Vektorin suuruuden laskemiseen käytetään erilaisia ​​kaavoja, joista osa on,

  • |A| = √(x 2 + ja 2 + z 2 ) kun vektori on muodossa A = xi + yj + zk
  • |A| = √((x) 2 + (ja) 2 ) kun vektori on annettu pisteellä A (x, y) ja origolla O(0, 0).
  • |A| = √((x 2 – x 1 ) 2 + (ja 2 - ja 1 ) 2 ) kun vektori on annettu pisteellä A (x1, ja2) ja piste B (x2, ja2).

Etsi vektori, jonka suuruus on 5.

On olemassa useita vektoreita, joiden magnitudi voi olla 5, joista esimerkki on vektori A, joka esitetään muodossa

A = 3i + 4j Tai A = 4i + 5j