Normaalivoima määritellään voimaksi, jonka mikä tahansa pinta kohdistaa toiseen esineeseen. Kun esine on levossa, siihen kohdistuva nettovoima on nolla. Normaalia voimaa ei voida kohdistaa kahteen pintaan, jotka eivät ole yhteydessä toisiinsa. Se voidaan tulkita voiman komponentiksi, joka on pystysuora mihin tahansa kosketuspintaan nähden. Se määrittää, kuinka paljon voimaa keho antaa maahan. Normaalivoima on yhtä suuri kuin kohteen paino vain, jos kohteen nopeuden muutosnopeus on negatiivinen, mikä tarkoittaa, että se hidastaa.

Kaava

Normaalivoiman arvo riippuu siitä, mihin kohde on sijoitettu suhteessa toiseen esineeseen. Kun esine putoaa, asento, jossa esine putoaa maahan, määrittää normaalivoiman arvon. Normaalivoima on merkitty symbolilla F_N. Sen mittayksikkö on Newton (N) ja mittakaava on [M¹L¹T^-2].

Jos kappale lepää tasaisella voimalla, normaalivoima on yhtä suuri kuin gravitaatiopainon arvo, eli mg.

F _N = mg

missä,

F_Non normaali voima,

m on lepäävän kohteen massa,

g on painovoiman aiheuttama kiihtyvyys.

Jos kappale liukuu alas vinolta pinnalta jossain kulmassa, normaalivoiman arvo on gravitaatiopaino, joka on lisätty F sin θ:n lisävoimalla. Tässä tapauksessa normaalivoima on suurempi kuin kohteen paino.

F _N = mg + F sin θ

Missä,

F_Non normaali voima,

m on liukuvan kohteen massa,

g on painovoiman aiheuttama kiihtyvyys,

θ on kaltevuuskulma.

Jos voima vaikuttaa kappaleeseen ylöspäin, normaalivoiman arvo on gravitaatiopaino vähennettynä voimalla F sin θ. Tässä tapauksessa normaali nettovoima on pienempi kuin kohteen paino.

F _N = mg – F sin θ

missä,

hakukone ja esimerkkejä

F_Non normaali voima,

m on liukuvan kohteen massa,

g on painovoiman aiheuttama kiihtyvyys,

θ on kaltevuuskulma.

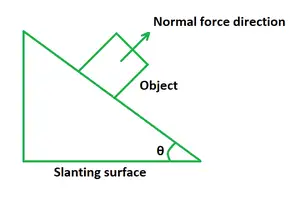
Jos kappale asetetaan kaltevalle tasolle, normaalivoima F_Non yhtä suuri kuin gravitaatiopainon ja kaltevuuskulman kosinin tulo.

F _N = mg cos θ

missä,

F_Non normaali voima,

m on liukuvan kohteen massa,

g on painovoiman aiheuttama kiihtyvyys,

θ on kaltevuuskulma.

Esimerkkiongelmat

Tehtävä 1. 2 kg painava esine lepää pöydällä. Laske siihen kohdistuva normaalivoima.

Ratkaisu:

Meillä on,

m = 2

g = 9,8

Käyttämällä kaavaa, jonka saamme,

F_N= mg

= 2 (9,8)

= 19,6 N

Tehtävä 2. Esine lepää pöydällä voimalla 39,2 N. Laske siihen kohdistuva normaalivoima.

Ratkaisu:

Meillä on,

F = 39,2

g = 9,8

Käyttämällä kaavaa, jonka saamme,

F_N= mg

=> m = F/g

=> m = 39,2/9,8

=> m = 4 kg

Tehtävä 3. 10 kg painava esine liukuu alas 200 N voimalla vinolta pinnalta 30° kulmassa. Laske siihen kohdistuva normaalivoima.

Ratkaisu:

Meillä on,

F = 200

m = 10

g = 9,8

θ = 30°

Käyttämällä kaavaa, jonka saamme,

F_N= mg + F sin θ

= 10 (9.8) + 200 sin 30°

= 98 + 200 (1/2)

= 98 + 100

= 198 N

Tehtävä 4. 20 kg painava esine liukuu alas 400 N voimalla vinolta pinnalta 30° kulmassa. Laske siihen kohdistuva normaalivoima.

Ratkaisu:

Meillä on,

F = 400

amplitudimodulaatio

m = 20

g = 9,8

θ = 30°

Käyttämällä kaavaa, jonka saamme,

F_N= mg + F sin θ

= 20 (9,8) + 400 ilman 30°

= 196 + 400 (1/2)

= 196 + 200

= 396 N

Tehtävä 5. 15 kg painava esine asetetaan vinolle pinnalle 30° kulmassa. Laske siihen kohdistuva normaalivoima, jos voima vaikuttaa ylöspäin arvolla 100 N.

Ratkaisu:

Meillä on,

muuntaa javassa merkkijonoksi

F = 100

m = 15

g = 9,8

θ = 30°

Käyttämällä kaavaa, jonka saamme,

F_N= mg – F sin θ

= 15 (9,8) – 100 ilman 30°

= 147 – 100 (1/2)

= 147-50

= 97 N

Tehtävä 6. 5 kg painava esine asetetaan vinolle pinnalle 60° kulmassa. Laske siihen missä tahansa kohdassa kohdistettu normaalivoima.

Ratkaisu:

Meillä on,

m = 5

g = 9,8

θ = 60°

Käyttämällä kaavaa, jonka saamme,

F_N= mg cos θ

= 5 (9,8) (cos 60°)

= 49/2

= 24,5 N

Tehtävä 7. Esine asetetaan vinolle pinnalle 60° kulmassa. Laske sen massa, jos siihen kohdistuva normaalivoima on 400 N.

Ratkaisu:

Meillä on,

F_N= 400,

θ = 60°

Käyttämällä kaavaa, jonka saamme,

F_N= mg cos θ

m = F/(g cos θ)

= 400/ (9,8 × cos 60°)

= 400/4,9

= 81,63 N