Sin Cos -kaavat trigonometriassa: Trigonometria on nimensä mukaisesti kolmioiden tutkimus. Se on tärkeä matematiikan haara, joka tutkii suoran kolmion sivujen pituuksien ja kulmien välistä suhdetta ja auttaa myös kolmion puuttuvien sivujen pituuksien tai kulmien määrittämisessä. On kuusi trigonometristä suhdetta tai funktiota: sini, kosini, tangentti, kosekantti, sekantti ja kotangentti, missä kosekantti, sekantti ja kotangentti ovat kolmen muun funktion, eli sinin, kosinin ja tangentin, vastavuoroiset funktiot.
Trigonometrinen suhde määritellään suorakulmaisen kolmion sivujen pituuksien suhteeksi. Trigonometriaa käytetään jokapäiväisessä elämässämme monilla aloilla. Se auttaa määrittämään kukkuloiden tai rakennusten korkeuden. Sitä käytetään myös aloilla, kuten kriminologia, rakentaminen, fysiikka, arkeologia, laivojen moottoritekniikka jne.
Tässä artikkelissa tutkimme kaikkea trigonometrian kaavat enimmäkseen sin- ja cos-kaavat esimerkeineen sekä luettelo kaikista trigonometrian kaavoista.
Sisällysluettelo
- Kaavat trigonometriassa
- Jotkut Sin Cosin peruskaavat
- Sin Cos -kaavataulukko
- Sin Cos -kaavojen esimerkkejä
- Harjoittele ongelmia Sin Cos -kaavoilla trigonometriassa esimerkkien kanssa
Kaavat trigonometriassa
Tarkastellaan suorakulmaista kolmiota XYZ, jossa ∠Y = 90°. Olkoon kulma kärjessä Z θ. θ:n viereistä puolta kutsutaan viereiseksi puolelle ja θ:n vastaista puolta vastakkaiseksi puolelle. Hypotenuusa on oikean kulman vastakkainen sivu tai suoran kulman pisin sivu.
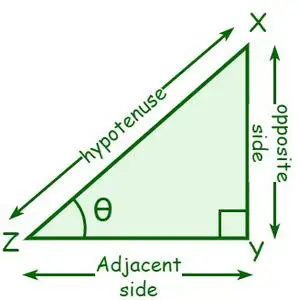
- sin θ = Vastakkainen puoli/hypotenuusa
- cos θ = Viereinen puoli/Hypotenuusa
- tan θ = vastakkainen puoli / viereinen puoli
- cosec θ = 1/sin θ = hypotenuusa/vastakkainen puoli
- sec θ = 1/ cos θ = hypotenuusa/viereinen puoli
- pinnasänky θ = 1/ rusketus θ = Viereinen puoli/vastakkainen puoli
Sine-kaava
Kulman sini suorakulmaisessa kolmiossa on vastakkaisen sivun pituuden suhde hypotenuusan pituuteen annettuun kulmaan. Sinifunktio esitetään syntinä.
sin θ = Vastakkainen puoli/hypotenuusa
Kosinin kaava
Kulman kosini suorakulmaisessa kolmiossa on viereisen sivun pituuden suhde hypotenuusan pituuteen annettuun kulmaan. Kosinifunktio esitetään muodossa cos.
lihavointi css:ssäcos θ = Viereinen puoli/Hypotenuusa
Jotkut Sin Cosin peruskaavat
Sini- ja kosinifunktiot kvadranteissa
- Sinifunktio on positiivinen ensimmäisessä ja toisessa kvadrantissa ja negatiivinen kolmannessa ja neljännessä neljänneksessä.
- Kosinifunktio on positiivinen ensimmäisessä ja neljännessä kvadrantissa ja negatiivinen toisessa ja kolmannessa neljänneksessä.
astetta
Kvadrantti
Sinifunktion merkki
Kosinifunktion merkki
0° - 90°
1. kvadrantti
+ (positiivinen)
+ (positiivinen)
90° - 180°
2. kvadrantti
+ (positiivinen)
– (negatiivinen)
180° - 270°
3. kvadrantti
– (negatiivinen)
– (negatiivinen)
270° - 360°
4. kvadrantti
– (negatiivinen)
+ (positiivinen)
Sini- ja kosinifunktioiden negatiivisen kulman identiteetti
- Negatiivisen kulman sini on aina yhtä suuri kuin kulman negatiivinen sini.
sin (– θ) = – sin θ
- Negatiivisen kulman kosini on aina yhtä suuri kuin kulman kosini.
cos (– θ) = cos θ
Sini- ja kosinifunktion välinen suhde
sin θ = cos (90° – θ)
Sini- ja kosinifunktioiden vastavuoroiset funktiot
- Kosekanttifunktio on sinifunktion käänteisfunktio.
cosec θ = 1/sin θ
- Sekanttifunktio on kosinifunktion käänteisfunktio.
sek θ = 1/cos θ
Pythagoralainen identiteetti
ilman 2 θ + cos 2 θ = 1
Sini- ja kosinifunktioiden jaksolliset identiteetit
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Double Angle -kaavat sini- ja kosinifunktioille
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – synti 2 θ = 2 cos 2 θ – 1 = 1 – 2 sin 2 i
Puolikulman identiteetit sini- ja kosinifunktioille
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Kolmikulmaiset identiteetit sini- ja kosinifunktioille
sin 3θ = 3 sin θ – 4 sin 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Summa- ja erotuskaavat
- Sinifunktio
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- Kosinifunktio
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Sinilaki eli sinisäännöt
Sinisäännön sinilaki on trigonometrinen laki, joka antaa suhteen kolmion sivujen pituuksien ja kulmien välillä.

a/sin A = b/sin B = c/sin C
Missä a, b ja c ovat kolmion ABC kolmen sivun pituudet ja A, B ja C ovat kulmia.
Kosinusten laki
Kosinisäännön kosinilakia käytetään määrittämään kolmion puuttuvat tai tuntemattomat kulmat tai sivujen pituudet.

a 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Missä a, b ja c ovat kolmion ABC kolmen sivun pituudet ja A, B ja C ovat kulmia.
Sin Cos -kaavataulukko
Tässä on Sin- ja Cos-kaavojen taulukko/luettelo eri kulmille asteina ja radiaaneina:
Sin Cosin kaavojen luettelo
| Kulma (asteina) | Kulma (radiaaneina) | synti i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Sin Cos -kaavojen esimerkkejä
Tehtävä 1: Jos cos α = 24/25, niin etsi sin α:n arvo.
Ratkaisu:
Annettu,
cos α = 24/25
Pythagoralaisista identiteeteistä, joita meillä on;
cos2θ + synti2θ = 1
(24/25)2+ ilman2α = 1
ilman2α = 1 – (24/25)2
ilman2α = 1 – (576/625) = (625 – 576)/625
ilman2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Siten sin α = ±7/25.
Tehtävä 2: Todista sin 2A ja cos 2A kaavat, jos ∠A= 30°.
Ratkaisu:
Annettu ∠A= 30°
Tiedämme sen,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Koska sin 30° = 1/2, cos 30° = √3/2 ja sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A-1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Koska cos 60° = 1/2 ja cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Siksi todistettu.
Tehtävä 3: Etsi cos x:n arvo, jos tan x = 3/4.
Ratkaisu:
Annettu, tan x = 3/4
Tiedämme sen,
tan x = vastakkainen puoli / viereinen puoli = 3/4
Hypotenuusan löytämiseksi käytämme Pythagoras-lausetta:
hypotenuusa2= päinvastoin2+ vierekkäin2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Nyt cos x = viereinen sivu/hypotenuusa
cos x = 4/5
Siten cos x:n arvo on 4/5.
Tehtävä 4: Etsi ∠C (asteina) ja ∠A (asteina), jos ∠B = 45°, BC = 15 tuumaa ja AC = 12 tuumaa.

Ratkaisu:
pikalajittelu
Annettu: ∠B = 45°, BC = a = 15 tuumaa ja AC = b = 12 tuumaa.
Sinilain laista, meillä on
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ ilman A = 15/16,97 = 0,8839
⇒ ∠A = synti-1(0,8839) = 62,11°
Tiedämme, että kolmion sisäkulmien summa on 180°.
Joten ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Näin ollen ∠A = 62,11° ja ∠C = 72,89°.
Tehtävä 5: Todista kosinifunktion puolikulmaiden identiteetit.
Ratkaisu:
Kosinifunktion puolikulman identiteetti on:
cos (θ/2) = ±√[(1 + cos θ)/2]
Kaksikulmaisista identiteeteistä meillä on
cos 2A = 2 cos2A-1
Korvaa nyt A:lla θ/2 molemmilla puolilla
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Siksi todistettu.
Harjoittele ongelmia Sin Cos -kaavoilla trigonometriassa esimerkkien kanssa
1. Annettu sin θ = 3/5. Etsi cos θ.
2. Todista identiteetti sin(2A) = 2 sinA cosA kun A=45∘.
3. Jos cos α = 5/13. Etsi synti(2a).
4. Ratkaise θ, jos sin θ = cos(90∘−θ).
5. Jos tan β = 2. Etsi sin β ja cos β käyttämällä Pythagoraan identiteettiä.
Usein kysytyt kysymykset Sin Cos -kaavoista trigonometriassa esimerkkien kanssa
Mitkä ovat trigonometrian perussini- ja kosinikaavat?
Perussini- ja kosinikaavat ovat sin θ = Vastakkainen/Hypotenuusa ja cos θ = Vierekkäinen/Hypotenuusa, missä θ on kulma suorakulmaisessa kolmiossa.
Miten löydät erikoiskulmien sinin ja kosinin?
Erikoiskulmilla, kuten 0∘, 30∘, 45∘, 60∘ ja 90∘, on tietyt sini- ja kosiniarvot, jotka voidaan muistaa trigonometristen taulukoiden tai yksikköympyrän käsitteiden avulla.
Mikä on sini- ja kosinifunktioiden välinen suhde?
Sini- ja kosinifunktiot liittyvät identiteettiin sin θ = cos(90∘- θ) ja pythagoralainen identiteetti ilman 2 θ+cos 2 θ = 1.
Kuinka käytät sinin ja kosinin kaksoiskulmakaavoja?
Kaksoiskulmakaavat ovat sin(2θ) = 2sinθcosθ ja cos(2θ)=cos 2 θ – synti 2 i. Näitä käytetään ilmaisemaan kaksoiskulmien trigonometriset funktiot yksittäisinä kulmina.
Kuinka löydät sinin ja kosinin arvot kulmille eri kvadranteissa?
Sini- ja kosinifunktioiden merkit riippuvat kvadrantista, jossa kulma sijaitsee:
- Ensimmäinen kvadrantti: sin θ> 0 ja cos θ> 0
- Toinen kvadrantti: sin θ> 0 ja cos θ < 0
- Kolmas kvadrantti: sinθ <0 ja cosθ < 0
- Neljäs kvadrantti: sinθ 0
