Matematiikassa kaikkialla on linjan toteutus. Se on toteutettu kaikkialla, eli geometriassa, algebrassa ja muissa. Kaltevuus määrittää viivan suunnan.
Tässä artikkelissa aiomme keskustella kahden tyyppisistä rinteistä, jotka ovat määrittelemätön kaltevuus ja nollakaltevuus. Ennen kuin ymmärrät kaltevuustyypit, katsotaanpa ensin kaltevuuden lyhyt kuvaus.
Mikä on rinne?
Kaltevuus määrittelee jyrkkyys linjasta. Sana 'jyrkkyys' tarkoittaa, kuinka paljon viiva on vino. Toisin sanoen kaltevuus osoittaa viivan suunnan koordinaattitasolla. Siksi se tunnetaan myös linjan gradientina. Ramppi, portaat jne. ovat joitain tosielämän esimerkkejä rinteestä.
natasha dalal
Matematiikassa kaltevuus on kahden pisteen välisen 'nousun' suhde 'juoksulla'. 'Nousu' tarkoittaa pystysuuntaista muutosta linjassa ja 'Run' tarkoittaa linjan vaakasuuntaista muutosta.
Kahden pisteen välisen viivan kaltevuus (x1, ja1) ja (x2, ja2) voidaan määrittää etsimällä pisteiden koordinaattien välinen ero. Viivan kaltevuus esitetään yleensä kirjaimella 'm'.
konstruktori javassam = Δx/Δy = (y2- ja1)/(x2- x1)
tai m = nousu/juoksu
Määrittelemätön kaltevuus
Määrittämätön kaltevuus on pystysuoran viivan kaltevuus. Tämä tarkoittaa, että jos viiva on pystysuora, kaltevuus on määrittelemätön. Määrittämättömän kaltevuuden viiva on yhdensuuntainen y-akselin kanssa ja ?x:n arvo on 0. Määrittämättömän kaltevuuden x-koordinaatti ei koskaan muutu riippumatta siitä, mikä y-koordinaatti on. Määrittämättömässä kulmakertoimessa Δy:n arvo on nollasta poikkeava kokonaisluku, kun taas Δx:n arvo on 0. Määrittelemätön kaltevuus on nollakulman vastakkainen. Nousussa ja juoksussa määrittämättömän kaltevuuden nousu on joko positiivinen tai negatiivinen, ja juoksu määrittelemättömässä kulmassa on nolla.
m = Δy/Δx = positiivinen tai negatiivinen Δy/0M:n määrittelemätön arvo edustaa määrittelemätöntä kaltevuutta ja pystysuoraa viivaa.
Seuraavassa kaaviossa voit nähdä määrittelemättömän kaltevuuden esityksen. Alla olevan kaavion viiva on yhdensuuntainen määrittelemätöntä kaltevuutta ilmaisevan y-akselin kanssa.
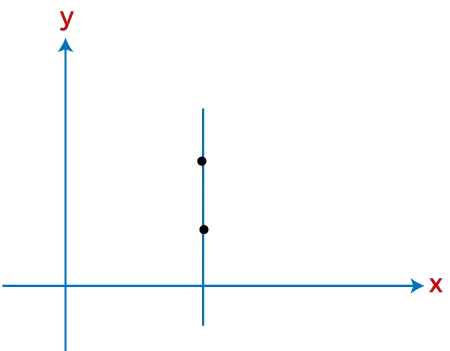
Kuva: Määrittämättömän kaltevuuden esitys
Yllä olevassa kuvassa on pystysuora viiva, joka osoittaa määrittelemättömän kaltevuuden.
Nolla kaltevuus
Nollakulmassa viiva on yhdensuuntainen x-akselin kanssa ja y-koordinaatti ei koskaan muutu. Se on vaakaviivan kaltevuus. Nousussa ja juoksussa nollakaltevuuden nousu on 0 ja nollakulman nousu on positiivinen.
Tuo skanneri javam = Δy/Δx = 0/positiivinen Δx
Jos m:n arvo on nolla, viiva on vaakasuora ja sen kaltevuus on vakio.
Seuraavassa kaaviossa näet nollakaltevuuden esityksen. Alla olevan kaavion viiva on yhdensuuntainen nollakulmaa ilmaisevan x-akselin kanssa, ja nollakulman y pysyy samana riippumatta x:stä.

Kuva: Nollakaltevuuden esitys
Yllä olevassa kuvassa on vaakasuora viiva, joka osoittaa nollakaltevuuden.
Katsotaan nyt ero määrittelemättömän kaltevuuden ja nollakaltevuuden välillä.
tulostustaulukko javassa
Ero määrittelemättömän kaltevuuden ja nollakaltevuuden välillä
Määrittelemätön kaltevuus on nollarinteen vastapäätä. Määrittämättömän kaltevuuden ja nollakaltevuuden välinen ero on taulukoitu seuraavasti -
| Kyllä ei. | Määrittelemätön kaltevuus | Nolla kaltevuus |
|---|---|---|
| 1. | Se määräytyy muuttujan X avulla. | Se määräytyy muuttujan Y avulla. |
| 2. | Se on pystysuoran viivan kaltevuus. | Se on vaakaviivan kaltevuus. |
| 3. | Määrittämättömällä rinteellä ei ole konkreettista arvoa, joten sillä on olematon arvo. | Nollakaltevuus on määrätty arvo, eli nolla. |
| 4. | Määrittämättömän kaltevuuden nimittäjä on nolla. | Nollakaltevuuden osoittaja on nolla. |
| 5. | Määrittämättömässä kulmakertoimessa Y muuttuu, mutta X ei muutu. | Määrittämättömässä kulmakertoimessa X muuttuu, mutta Y ei muutu. |
Siinä kaikki artikkelista. Olemme yrittäneet antaa sinulle riittävästi tietoa helpommin. Toivottavasti se on sinulle hyödyllistä ja antaa sinulle tietoa määrittelemättömästä kaltevasta, nollakalteesta ja niiden vertailusta.
