Pallon tilavuus on nesteen määrä, jonka pallo voi sisältää. Pallon kaavan tilavuus annetaan muodossa 4/3πr³. Se on tila, jonka pallo on 3-ulotteisessa avaruudessa. Se mitataan yksiköissä³eli m³, cm³jne. Pallo on kolmiulotteinen kiinteä esine, jonka geometria on pyöreä.

Pallon tilavuus on pallon pinnan kokonaistilavuus ja se on verrannollinen pallon säteen kuutioon. Tässä artikkelissa opimme tarkemmin Pallon tilavuudesta, Pallokaavan tilavuudesta, Pallokaavan tilavuudesta ja muista yksityiskohtaisesti.

• Mikä on pallon tilavuus?
• Pallokaavan tilavuus
• Kiinteän pallon tilavuus
• Onton pallon tilavuus
• Pallokaavan johtamisen määrä
• Kuinka laskea pallon tilavuus?

Mikä on pallon tilavuus?

Pallon tilavuus on tilan määrä, jonka se vie sisällään. Pallo on kolmiulotteinen pyöreä kiinteä muoto, jossa kaikki sen pinnan pisteet ovat yhtä kaukana sen keskustasta. Kiinteä etäisyys on pallon säde ja kiinteä piste on pallon keskipiste. Huomaamme muodon muutoksen, kun ympyrää käännetään. Ympyränä tunnetun kaksiulotteisen kohteen pyörimisen tuloksena saadaan pallon kolmiulotteinen muoto.

Lisätietoja,

• Pallo
• Pallon pinta-ala

Pallon tilavuuden määritelmä

Pallon tilavuus on pallon pinnan ympäröimä kokonaismassa. Se on 3D-avaruus pallon sisällä. Se riippuu pallon säteestä. Alla lisätyssä kuvassa näkyy pallo, jonka säde on r ja sen tilavuus.

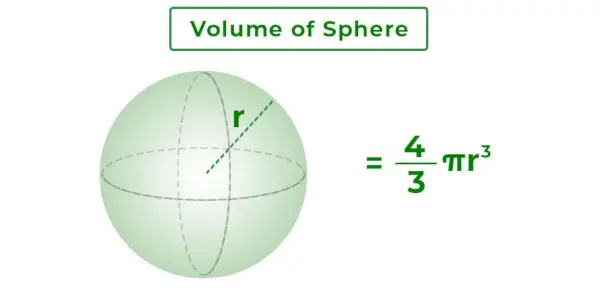
Pallokaavan tilavuus

Pallon tilavuuskaava on kaava, jota käytetään pallon tilavuuden selvittämiseen, kun sen säde on annettu. Säteen R pallon kaavan tilavuus lisätään alle,

Pallokaavan tilavuus = 4/3πr ³

Missä,

• r on pallon säde
• Pi on vakio ja sen arvo on 22/7

Pallo luokitellaan yleensä kahteen osaan, jotka ovat

• Kiinteän pallon tilavuus
• Onton pallon tilavuus

Opitaanpa niistä yksityiskohtaisesti.

Kiinteän pallon tilavuus

Kiinteä pallo on pallo, joka on täysin täytetty sisälle asti. eli sillä on massa ytimeen asti ja kaava tilavuudelle, kun sen säde on r on,

Kiinteän pallon tilavuus(V) = (4/3)πr ³

Onton pallon tilavuus

Ontolla pallolla sen sisätila on tyhjä ja oletetaan, että sen ulkosäde on R ja sen sisäsäde on r, sitten sen tilavuus lasketaan kaavalla,

Onton pallon tilavuus = (4/3)π(R ³ – r ³ )

Pallokaavan johtamisen määrä

Pallokaavan tilavuus voidaan johtaa seuraavilla menetelmillä:

• Integroinnin käyttäminen
• Arkhimedesen käyttäminen sylinterin, kartion ja pallon välistä suhdetta

Tarkastellaan näitä menetelmiä yksityiskohtaisesti seuraavasti:

Integrointia käyttävän pallon tilavuus

Integrointimenetelmää käyttämällä voimme yksinkertaisesti laskea pallon tilavuuden.

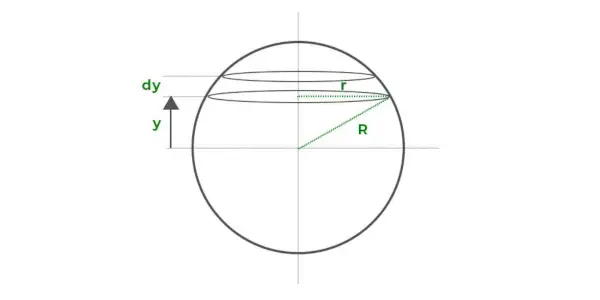
Oletetaan, että pallon tilavuus koostuu sarjasta ohuita pyöreitä kiekkoja, jotka on pinottu päällekkäin yllä olevan kaavion mukaisesti. Jokaisen ohuen kiekon säde on r ja dy:n ​​paksuus, joka on y:n etäisyydellä x-akselista.

Olkoon levyn äänenvoimakkuus dV. dV:n arvo saadaan kaavalla,

dV = (πr²) sinä

Siten dV = π (R²- ja²) sinä

Pallon kokonaistilavuus on kaikkien näiden pienten levyjen tilavuuksien summa. Tarvittava arvo saadaan integroimalla lauseke rajasta -R arvoon R.

Joten pallon tilavuudesta tulee

V =int_{y=-R}^{y=R} dV

⇒ V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V =pi left[2R^3-frac{2R^3}{3} ight]

⇒ V =frac{4}{3}pi R^3

Siten johdetaan pallon tilavuuden kaava.

Pallon tilavuus Archimedes-suhteiden avulla

Kuten Archimedes on jo osoittanut, jos kartiolla, pallolla ja sylinterillä on sama säde r ja sama korkeus, niiden tilavuudet ovat suhteessa 1:2:3.

Siksi voimme sanoa:

Sylinterin tilavuus = Kartion tilavuus + Pallon tilavuus

Siten Pallon tilavuus = Sylinterin tilavuus – Kartion tilavuus

Kuten tiedämme, tuo sylinterin tilavuus = πr²h ja kartion tilavuus = (1/3)πr²h

Korvaamalla nämä arvot yhtälöön, saamme:

Pallon tilavuus = πr²h – (1/3)πr²h = (2/3)πr²h

Oletetaan, että sylinterin korkeus on yhtä suuri kuin pallon halkaisija, joka on 2r. Täten:

Pallon tilavuus on (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Myös Tarkista

• Pallomainen korkki Volume Formula
• Pallomainen sektorin kaava
• Pallomaisen segmentin kaava

Kuinka laskea pallon tilavuus?

Pallon tilavuus on pallon miehittämä tila. Sen tilavuus voidaan laskea kaavalla V = 4/3πr ³ .

Pallon tilavuuden laskemiseen vaadittavat vaiheet ovat:

Vaihe 1: Merkitse pallon säteen arvo.

2. syyskuuta: Etsi säteen kuutio.

Vaihe 3: Kerro säteen kuutio arvolla (4/3)π

Vaihe 4: Lisää (yksikkö)³lopulliseen vastaukseen.

Esimerkki pallon tilavuuden laskemiseksi

Esimerkki: Etsi pallon tilavuus, jonka säde on 7 cm.

Annettu, r = 7 cm

V = (4/3)πr³

Pallon tilavuus, V = ((4/3) × π × 7³) cm³

Korkeus = 1436,8 cm³

Siten pallon tilavuus on 1436,8 cm³

Lue lisää

• Kartion tilavuus
• Kuution tilavuus
• Sylinterin tilavuus

Palloesimerkkien määrä

Esimerkki 1. Etsi sen pallon tilavuus, jonka säde on 9 cm.

Ratkaisu:

Meillä on r = 9

Pallon tilavuus = 4/3 πr³

⇒ Pallon tilavuus = (4/3) (3.14) (9) (9) (9)

⇒ Pallon tilavuus = (4) (3.14) (3) (9) (9)

⇒ Pallon tilavuus = 3052 cm³

Esimerkki 2. Etsi sen pallon tilavuus, jonka säde on 12 cm.

Ratkaisu:

Meillä on r = 12

Pallon tilavuus = 4/3 πr³

⇒ Pallon tilavuus = (4/3) (3.14) (12) (12) (12)

⇒ Pallon tilavuus = (4) (3.14) (4) (12) (12)

⇒ Pallon tilavuus = 7234,56 cm³

Esimerkki 3. Etsi sen pallon tilavuus, jonka säde on 6 cm.

Ratkaisu:

Meillä on r = 6

Pallon tilavuus = 4/3 πr³

⇒ Pallon tilavuus = (4/3) (3.14) (6) (6) (6)

⇒ Pallon tilavuus = (4) (3.14) (2) (6) (6)

⇒ Pallon tilavuus = 904,32 cm³

Esimerkki 4. Etsi sen pallon tilavuus, jonka säde on 4 cm.

Ratkaisu:

Meillä on r = 4

Pallon tilavuus = 4/3 πr3

⇒ Pallon tilavuus = (4/3) (3.14) (4) (4) (4)

⇒ Pallon tilavuus = (1.33) (3.14) (4) (4) (4)

⇒ Pallon tilavuus = 267,27 cm³

Esimerkki 5. Laske pallon tilavuus, jonka halkaisija on 10 cm.

Ratkaisu:

Meillä on 2r = 10

mikä on map java

⇒ r = 5

Pallon tilavuus = 4/3 πr³

⇒ Pallon tilavuus = (4/3) (3.14) (5) (5) (5)

⇒ Pallon tilavuus = (1.33) (3.14) (5) (5) (5)

⇒ Pallon tilavuus = 522,025 cm³

Esimerkki 6. Laske pallon tilavuus, jonka halkaisija on 16 cm.

Ratkaisu:

Meillä on 2r = 16

⇒ r = 8

Pallon tilavuus = 4/3 πr³

⇒ Pallon tilavuus = (4/3) (3.14) (8) (8) (8)

⇒ Pallon tilavuus = (1.33) (3.14) (8) (8) (8)

⇒ Pallon tilavuus = 2138,21 cm³

Esimerkki 7. Laske pallon tilavuus, jonka halkaisija on 14 cm.

Ratkaisu:

Meillä on 2r = 14

⇒ r = 7

Pallon tilavuus = 4/3 πr³

⇒ Pallon tilavuus = (4/3) (3.14) (7) (7) (7)

⇒ Pallon tilavuus = (1.33) (3.14) (7) (7) (7)

⇒ Pallon tilavuus = 1432,43 cm³

Osa sfääri-harjoittelukysymyksiä

Q1: Laske pallon tilavuus, jonka halkaisija on 34 cm.

Q2: Laske onton pallon tilavuus, jonka sisähalkaisija on 4 cm ja ulkosäde 8 cm.

Q3: Etsi sen pallon tilavuus, jonka säde on 14 cm.

Q4: Mikä on pallon tilavuus, jonka säde on yhtä suuri kuin neliön sivu, jonka pinta-ala on 144 m².

Sphere-FAQ:n määrä

Mikä on pallon tilavuus?

Pallon tilavuus on pallon pinnan viemä tila.

Mikä on pallokaavan pinta-ala?

Pallon kokonaispinta-ala, jonka säde on r, on, Pinta-ala = 4πr ²

Mikä on pallon tilavuuden kaava?

Pallon tilavuus, jonka säde on r, on, Tilavuus = 4/3πr ³

Kuinka löydämme pallonpuoliskon tilavuuden?

Puolipallon, jonka säde on r, tilavuus on, Tilavuus = 2/3πr ³

Mikä on pallon ja pallonpuoliskon tilavuuden suhde?

Jos pallon ja puolipallon säteet ovat samat, niiden tilavuuden suhde on

SISÄÄN ₁ : SISÄÄN ₂ = (4/3πr ³ ): (2/3πr ³ ) = 2:1

Mikä on pallon tilavuusyksikkö?

Pallon tilavuus mitataan metreinä³, cm³, litraa jne. m ³ on vakiomittayksikkö.

Mikä on pallon tilavuus, kun sen säde on puolitettu?

Pallon tilavuus = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Volume/8. Joten pallon tilavuudesta tulee yksi kahdeksasosa.