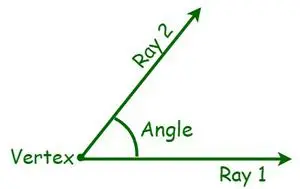
Geometriassa kulma on geometrisen muodon olennainen mitta. Kulma määritellään kiertymisasteeksi kahden suoran tai tason välisen leikkauspisteen ympärillä, jotka vaaditaan saattamaan toinen vastaamaan toista. Kulmia on erilaisia kulman mittauksen perusteella. Se mitataan asteina tai radiaaneina. Kulma on muoto, joka muodostuu kahdesta suorasta tai säteestä, jotka eroavat yhteisestä pisteestä, jota kutsutaan kärjeksi. Kun kaksi sädettä leikataan, eli kun puolisuorat projisoidaan yhteisellä päätepisteellä, muodostuu kulma. Nyt yleisiä päätepisteitä kutsutaan kärkipisteiksi, kun taas säteet tunnetaan käsivarsina.
Kulmien tyypit

- Terävä kulma: Terävä kulma on kulma, joka on suurempi kuin 0 astetta ja pienempi kuin 90 astetta, eli se vaihtelee välillä 0° - 90° (molemmat ilman).
- Oikea kulma: Suoraa kulmaa kutsutaan kulmaksi, joka mittaa täsmälleen 90 astetta.
- Tylppä kulma: Tylsä kulma on kulma, joka on suurempi kuin 90 astetta ja pienempi kuin 180 astetta, eli se vaihtelee välillä 90° - 180° (molemmat ilman).
- Suorakulma: Suoraa kulmaa kutsutaan kulmaksi, joka on täsmälleen 180 astetta.
- Kupera kulma: Refleksikulma on kulma, joka on suurempi kuin 180 astetta ja pienempi kuin 360 astetta, eli se vaihtelee välillä 180° - 360° (molemmat ilman).
- Täysi kulma tai täysi kierto: Täydellistä kulmaa kutsutaan kulmaksi, joka mittaa täsmälleen 360 astetta.
On myös muita kulmia, kuten täydentäviä kulmia, lisäkulmia sekä vierekkäisiä ja ei-vierekkäisiä kulmia.
- Täydentävät kulmat: Kahden kulman sanotaan olevan toisiaan täydentäviä, jos niiden summa on suora kulma, eli 90°.
- Lisäkulmat: Kahden kulman sanotaan olevan täydentäviä, jos niiden summa on 180°.
- Vierekkäiset kulmat: Kahden kulman sanotaan olevan vierekkäin, jos niillä on yhteinen kärki ja yhteinen haara.
- Ei vierekkäiset kulmat: Kahden kulman sanotaan olevan ei-vierekkäinen, jos niillä ei ole yhteistä kärkeä ja yhteistä haaraa.
Kaava kulmien etsimiseen
On olemassa erilaisia kaavoja kulman löytämiseksi; Jotkut niistä ovat keskikulmakaava, kaksoiskulmakaava, puolikulmakaava, yhdistekulmakaava, sisäkulmakaava jne.
- Käytämme keskikulmakaavaa määrittääksemme ympyrään tehdyn segmentin kulman.
- Käytämme sisäkulmien summaa monikulmion puuttuvan kulman määrittämiseen.
- Käytämme trigonometrisiä suhteita löytääksemme suorakulmaisen kolmion puuttuvan kulman.
- Käytämme sini- tai kosinilakia löytääksemme ei-suorakulmaisen kolmion puuttuvan kulman.
Kaavan nimi | Kaava | Kuinka löytää tuntematon kulma? |
|---|---|---|
| Keskikulman kaava | θ =(s × 360°)/2prTässä s on kaaren pituus ja r on ympyrän säde | Korvaa kaaren pituuden ja ympyrän säteen arvot määrittääksesi ympyrän janan kulman. |
| Sisäkulmien summa Kaava | 180° (n-2)Tässä n on monikulmion sivujen lukumäärä | Monikulmion tuntemattoman sisäkulman määrittämiseksi laske ensin kaikkien sisäkulmien summa tämän kaavan avulla ja vähennä sitten tuloksesta kaikkien tunnettujen kulmien summa. |
| Trigonometriset suhteet | sin θ = vastakkainen puoli/hypotenuusacos θ = viereinen sivu/hypotenuusatan θ = vastakkainen puoli / viereinen puoli | Riippuen suorakulmaisen kolmion käytettävissä olevista kahdesta sivusta, valitse yksi näistä trigonometrisista suhteista löytääksesi tuntemattoman kulman. mylivecricket live-kriketissä |
| Sinesin laki | a/sin A = b/sin B = c/sin CTässä A, B ja C ovat kolmion sisäkulmat ja a, b ja c ovat niiden vastakkaiset sivut. | Kun tunnemme kaksi sivua ja sisällyttämätön kulma (tai) kaksi kulmaa ja sisällyttämätön sivu, niin kolmion tuntemattomien kulmien määrittämiseen voidaan käyttää sinien lakia. |
| Kosinusten laki | a2= b2+ c2– 2bc cos Ab2= c2+ a2– 2ca cos Bc2= a2+ b2– 2ab cos CTässä A, B ja C ovat kolmion sisäkulmat ja a, b ja c ovat niiden vastakkaiset sivut. | Kun tunnemme kolme sivua (tai) kaksi sivua ja sisällytetty kulma, niin kosinilakia voidaan käyttää kolmion tuntemattomien kulmien määrittämiseen. |
Esimerkkikysymykset
Kysymys 1: Etsi annetun kolmion kärjen B kulma käyttämällä jotakin trigonometrisista kaavoista kulmien etsimiseen.

Ratkaisu:
Annettu,
BC = 3 yksikköä = θ:n viereinen puoli.
AC = 4 yksikköä = θ:n vastakkainen puoli.
Tässä tapauksessa tunnemme sekä θ:n vastakkaiset että vierekkäiset puolet. Tästä syystä voimme käyttää tangenttikaavaa löytääksemme θ:n.
⇒ tan θ = vastakkainen puoli / viereinen puoli
⇒ tan θ = 4/3
⇒ θ = ruskea-1(4/3) ⇒ θ = 53,1°
Siten kulma kärjessä B on 53,1°.
Kysymys 2: Etsi kulmat pisteissä X ja Y, jos ∠Z = 35° ja x = 3 tuumaa, y = 8 tuumaa ja z = 3,5 tuumaa.

Ratkaisu:
Annettu,
∠Z = 35° ja x = 6 tuumaa, y = 3 tuumaa ja z = 3,5 tuumaa
Koska tunnemme kaikki kolme sivua ja kulman, voimme käyttää sinisäännön kaavaa.
Meillä on sinisäännön kaavasta
x/sin X = y/sin Y = z/sin Z
Nyt,
y/sin Y = z/sin Z
javascript-kutsutoiminto html:stä⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/ilman Y = 3,5/0,574 {Koska sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = synti−1(0,492) = 29,47°
Tiedämme, että kolmen kulman summa kolmiossa on 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Näin ollen ∠X = 115,53° ja ∠Y = 29,47°.
Kysymys 3: Laske viisikulmion viides sisäkulma, jos sen neljä sisäkulmaa ovat 110°, 85°, 136° ja 105°.
Ratkaisu:
Viisikulmion sivujen lukumäärä (n) = 5.
Nyt viisikulmion kaikkien 5 sisäkulman summa = 180 (n -2)°
= 180 (5-2)° = 540°.
Annettujen 4 sisäkulman summa = 110°+ 85°+ 136°+ ja 105°= 436°.
Eli viides sisäkulma = 540° – 436° = 104°
Siten viisikulmion viides sisäkulma on 104°.
Kysymys 4: Määritä y:n arvo ja myös kulmien mitta annetusta kuvasta.

Ratkaisu:
Annetusta kuvasta voidaan havaita, että (4y – 6)° ja (3y + 5)° ovat komplementaarisia kulmia, eli (4y – 6)°:n ja (3y + 5)°:n summa on 90 °.
⇒ (4v – 6)° + (3v + 5)° = 90°
⇒ (7v – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Nyt (4v – 6)° = (4 × 13 – 6)° = (52–6)° = 46°
(3v + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Kysymys 5: Etsi annetun kolmion kärjen Q kulma käyttämällä jotakin kulmien etsintäkaavaa.

Ratkaisu:
Annettu p = QR = 6 cm, q = PR = 9 cm ja r = PQ = 7 cm.
Koska tunnemme kaikki kolme sivua ja kulman, voimme käyttää kosinisäännön kaavaa löytääksemme kulman kärjen Q.
⇒ q2= s2+ r2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6) (7) cos Q
⇒ 81 = 36 + 49 - 84 cos Q
⇒ 81 = 85 - 84cos Q
⇒84 cos Q = 81–85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Siten kulma kärjessä Q, ∠Q = 92,72°.
Kysymys 6: Laske ympyrän janan kulma, jos kaaren pituus on 12π ja säde 9 cm.
kuinka tietää, onko joku estänyt sinut Androidissa
Ratkaisu:
Annettu,
Kaaren pituus = 12π
Säde (r) = 9 cm
Nyt kulmakaava on:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 × 360°/10
⇒ θ = 240°
Näin ollen kulma on 240°.
