Kahden vektorin välinen kulma on niiden pyrstöjen välinen kulma, ja tämä kulma voidaan helposti löytää käyttämällä vektorikaavojen ristituloa ja pistetuloa. Kahden vektorin välinen kulma on aina välillä 0° - 180°.

Tässä artikkelissa opimme yksityiskohtaisesti kahden vektorin välisestä kulmasta, määritelmästä, kaavoista ja esimerkeistä.

Mikä on kahden vektorin välinen kulma?

Kahden vektorin välinen kulma on kulma, joka muodostuu niiden pyrstöjen leikkauspisteestä. Kahden vektorin välinen kulma voi olla akuutti, oikea tai tylppä vektorien suunnasta riippuen.

Kahden vektorin välinen kulma löydetään kahdella kaavalla:

• Vektorien pistetulon käyttäminen
• Vektorien ristitulon käyttäminen

Tämä selitetään alla olevassa kaavassa.

Kulma kahden vektorin kaavat

Kahden vektorin välinen kulma löytyy helposti ja yleisimmin käyttämällä vektoreiden skalaarituloa.

Kaksi vektoria A ja B

Pistetuote A:n ja B:n antaa,

bash lukea tiedosto

vec{A}.vec{B} = |A| |B| cosθ.

Erikoistapaukset

• Kun vektorien välinen kulma on 0 astetta.

Eli θ = 0°

⇒ |A| |B| cosθ

⇒ |A| |B| cos0°

⇒ |A| |B| [cos0° = 1]

• Kun vektorien välinen kulma on 180 astetta.

⇒ |A| |B| cosθ

⇒ |A| |B| cos180°

⇒ – |A| |B| [cos180° = -1]

• Kun vektorien välinen kulma on 90 astetta.

⇒ |A| |B| cosθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

Kahden vektorin välisen kulman kaava

Kahden vektorin välisen kulman kosini on yhtä suuri kuin näiden kahden vektorin yksittäisten ainesosien tulon summa jaettuna näiden kahden vektorin suuruuden tulolla.

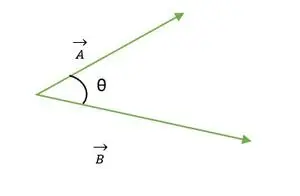
Kaksi vektoria A ja B

vec{A}.vec{B} =| A | | B | cosθ.

cosθ=frac{vec{A}.vec{B}}B

θ = cos^-1 frac{vec{A}.vec{B}}B

karteesisessa muodossa,

A = A_xi + A_jaj + A_Kanssak

B = B_xi + B_jaj + B_Kanssak

cos θ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Dot-tuotteen ominaisuudet

• Pistetulo on kommutiivinen

vec{A}.vec{B}=vec{B}.vec{A}

• Pistetuote on jakelua edistävä

vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})

Kahden vektorin välinen kulma on välillä 0 ≤ θ ≤ 180. Kun molempien vektorien päät tai päät ovat yhtenevät, vektorien välinen kulma lasketaan.

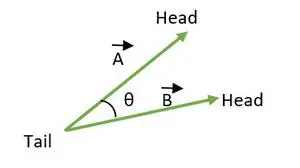
Häntä sama

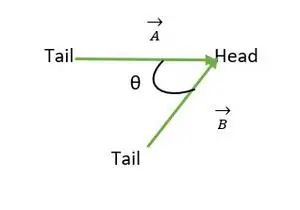
Pää täsmää

Esimerkkitehtävät Kahden vektorin välinen kulma -kaava

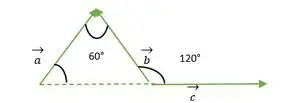
Tehtävä 1: Etsi vektoreiden välinen kulma (jos ne muodostavat tasasivuisen kolmion)

• a- ja b-vektorit
• b- ja c-vektorit
• a- ja c-vektorit

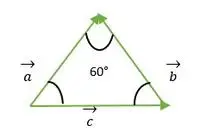
Tasasivuinen kolmio, jonka muodostavat vektorit a, b, c

Ratkaisu:

• a- ja b-vektorit

Vektorille a ja b molempien vektorien pää osuu yhteen, joten vektorin a ja b välinen kulma on sama kuin tasasivuisen kolmion kahden sivun välinen kulma = 60°.

• b- ja c-vektorit:

Yllä olevasta kuvasta näemme, että b- ja c-vektorin pää tai häntä eivät täsmää toistensa kanssa.

median siirto

Joten käyttämällä ominaisuutta- A vektori pysyy muuttumattomana, jos se lähetetään rinnakkain itsensä kanssa.

Vektori c siirretään yhdensuuntaisesti itsensä kanssa

Nyt näemme vektorien b ja c pään osuvan yhteen, joten se on sama kuin ulkokulma make tasasivuisen kolmion kanssa = 120°.

• a- ja c-vektorit

A:n ja c:n häntä ovat samat

Vektoreilla a ja c molempien vektorien pyrstö osuu yhteen, joten vektorien a ja c välinen kulma on sama kuin tasasivuisen kolmion kahden sivun välinen kulma = 60°.

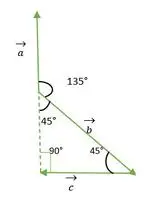
Tehtävä 2: Etsi kulmat vektorien välillä, jos ne muodostavat tasakylkisen suorakulmaisen kolmion.

• a- ja b-vektori
• b- ja c-vektori
• a- ja c-vektorit

Ratkaisu:

• a- ja b-vektori

Suorakulmainen tasakylkinen kolmio

Yllä olevasta kuvasta näemme, että a- ja b-vektorin pää tai häntä eivät täsmää toistensa kanssa. Joten käyttämällä ominaisuutta- A vektori pysyy muuttumattomana, jos se lähetetään rinnakkain itsensä kanssa.

vektoria siirretään yhdensuuntaisesti itsensä kanssa

Nyt a- ja b-vektorien hännän osuvat toistensa kanssa yhteen ja muodostavat kulman, joka on sama kuin suorakulmaisen tasakylkisen kolmion ulkokulma = 135°.

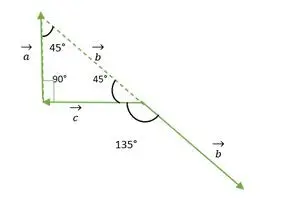
• b- ja c-vektori

Suorakulmainen tasakylkinen kolmio

Yllä olevasta kuvasta b- ja c-vektorin pää tai hännät eivät täsmää toistensa kanssa. Joten ominaisuutta käyttämällä vektori pysyy muuttumattomana, jos se lähetetään rinnakkain itsensä kanssa.

b-vektoria siirretään yhdensuuntaisesti itsensä kanssa

Nyt b- ja c-vektorien hännän osuvat toisiinsa ja muodostavat kulman, joka on sama kuin suorakulmaisen tasakylkisen kolmion ulkokulma = 135°.

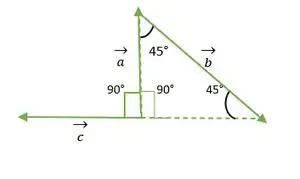
• a- ja c-vektorit

Suorakulmainen tasakylkinen kolmio

Yllä olevasta kuvasta a- ja c-vektorin pää tai pyrstö eivät täsmää toistensa kanssa. Joten käyttämällä ominaisuutta- A vektori pysyy muuttumattomana, jos se lähetetään rinnakkain itsensä kanssa.

c-vektoria siirretään yhdensuuntaisesti itsensä kanssa

Nyt a- ja c-vektorien hännän osuvat toisiinsa ja muodostavat kulman, joka on sama kuin tasakylkisen kolmion oikea kulma = 90°.

Tehtävä 3: Etsi kulma vektorien A = i + j + k ja vektorin B = -2i – 2j – 2k välillä.

Ratkaisu:

Kaavasta,

A = A_xi + A_jaj + A_Kanssak

B = B_xi + B_jaj + B_Kanssak

cosθ=frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tässä Annetussa kysymyksessä

A = i + j + k

B = -2i -2j -2k

Arvojen korvaaminen kaavassa

string.substring java

⇒ cosθ =frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})}

⇒ cosθ =frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})}

⇒ cosθ =frac{-6}{(sqrt{3}×sqrt{12})}

⇒ cosθ =frac{-6}{(sqrt{36})}

⇒ cosθ = -6/6

⇒ cosθ= -1

⇒ θ = 180°

Tehtävä 4: Etsi kulma vektorien A = 3i + 4j ja B = 2i + j välillä

Ratkaisu:

A = A_xi + A_jaj + A_Kanssak

B = B_xi + B_jaj + B_Kanssak

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tässä annettu,

A = 3i + 4j + 0k

B = 2i + j + 0k

Korvaa arvot kaavassa,

⇒ cosθ =frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})}

⇒ cosθ =frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})}

⇒ cosθ =frac{(10)}{(sqrt{25}×sqrt{5})}

⇒ cosθ =frac{(10)}{(sqrt{125})}

⇒ θ = cos^-1(frac{(10)}{5.(sqrt{5})})

jännä kieli

⇒ θ = cos^-1(frac{2}{(sqrt{5})})

Tehtävä 5: Etsi kulma vektorin A = i + j ja vektorin B = j + k välillä.

Ratkaisu:

Kaavasta,

A = A_xi + A_jaj + A_Kanssak

B = B_xi + B_jaj + B_Kanssak

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tässä Annetussa kysymyksessä

⇒ A = i + j

⇒ B = j + k

⇒ cosθ =frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})}

⇒ cosθ =frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})}

⇒ cosθ =frac{1}{(sqrt{2}×sqrt{2})}

⇒ θ = cos^-1(1/2)

⇒ θ = 60°