Enkooderi on digitaalinen piiri, joka muuntaa joukon binäärituloja ainutlaatuiseksi binäärikoodiksi. Binäärikoodi edustaa tulon sijaintia ja sitä käytetään tunnistamaan tietty aktiivinen tulo. Enkoodeja käytetään yleisesti digitaalisissa järjestelmissä rinnakkaisten tulojen muuntamiseen sarjakoodiksi.
Enkooderin perusperiaate on määrittää yksilöllinen binäärikoodi jokaiselle mahdolliselle tulolle. Esimerkiksi 2-4-linjaisessa kooderissa on 2 tulolinjaa ja 4 lähtölinjaa ja se määrittää yksilöllisen 4-bittisen binaarikoodin kullekin 2^2 = 4 mahdollisesta tuloyhdistelmästä. Anturin lähtö on yleensä aktiivinen matala, mikä tarkoittaa, että vain yksi lähtö on aktiivinen (matala) kulloinkin ja loput lähdöt ovat passiivisia (high). Aktiivinen matala lähtö valitaan aktiiviselle tulolle määritetyn binäärikoodin perusteella.
On olemassa erilaisia koodereita, mukaan lukien prioriteettikooderit, jotka määrittävät prioriteetin jokaiselle tulolle, ja binääripainotetut kooderit, jotka käyttävät binääripainotusjärjestelmää binäärikoodien osoittamiseen tuloille. Yhteenvetona voidaan todeta, että kooderi on digitaalinen piiri, joka muuntaa joukon binäärituloja ainutlaatuiseksi binäärikoodiksi, joka edustaa tulon sijaintia. Enkoodeja käytetään laajalti digitaalisissa järjestelmissä rinnakkaisten tulojen muuntamiseksi sarjakoodeiksi.
Enkooderi on a yhdistelmäpiiri joka suorittaa käänteisen toiminnon a Dekooderi . Siinä on enintään 2^n syöttöriviä ja 'n' lähtöriviä , joten se koodaa 2^n tulon tiedot n-bittiseksi koodiksi. Se tuottaa binäärikoodin, joka vastaa tuloa, joka on aktiivinen High. Siksi kooderi koodaa 2^n tulolinjaa 'n'-bitillä.
Enkooderi
Enkooderityypit
On olemassa erilaisia koodereita, jotka on mainittu alla.
string.valueof java
- 4-2 Enkooderi
- Octal to Binary Encoder (8-3 Enkooderi)
- Desimaalista BCD-enkooderiin
- Priority Encoder
4-2 Enkooderi
4-2 Encoder koostuu neljä tuloa Y3, Y2, Y1 & Y0 ja kaksi lähtöä A1 ja A0 . Milloin tahansa näistä neljästä sisääntulosta vain yksi voi olla '1', jotta vastaava binäärikoodi saadaan ulostuloon. Alla olevassa kuvassa näkyy 4-2-anturin logiikkasymboli.
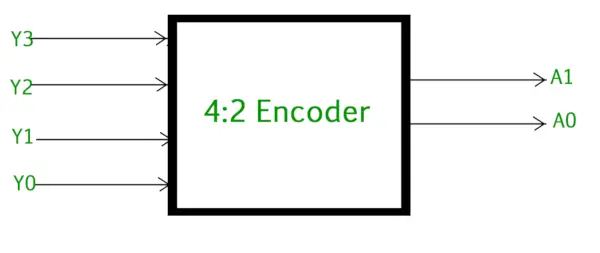
4-2 Enkooderi
Totuustaulukko 4-2 enkooderista on seuraava.
on proteiinirasvaa
| INPUTS | TUOTTEET | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Looginen lauseke A1:lle ja A0:lle:
A1 = Y3 + Y2 A0 = Y3 + Y1>
Yllä olevat kaksi Boolen funktiota A1 ja A0 voidaan toteuttaa käyttämällä kahta tulo TAI -porttia:
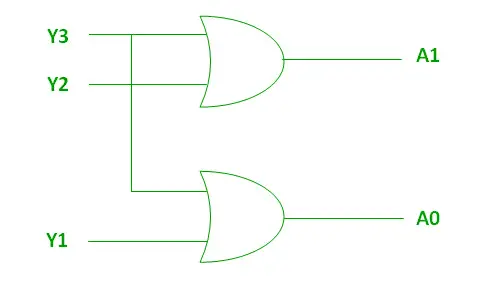
Toteutus OR-portin avulla
Octal to Binary Encoder (8-3 Enkooderi)
8-3 Enkooderi tai oktaalista binaarikooderiin koostuu 8 sisääntuloa : Y7 - Y0 ja 3 lähtöä : A2, A1 & A0. Jokainen tulorivi vastaa jokaista oktaalilukua ja kolme lähtöä muodostavat vastaavan binaarikoodin. Alla olevassa kuvassa näkyy oktaalin logiikkasymboli binäärikooderille.
java saada nykyinen päivämäärä
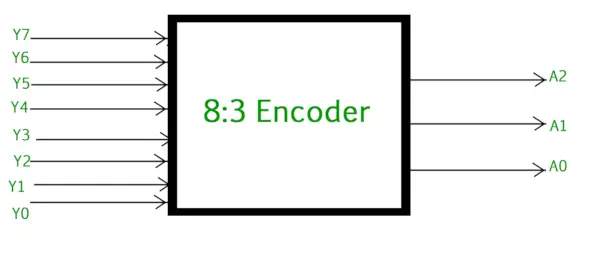
Octal to Binary Encoder (8-3 Enkooderi)
Totuustaulukko 8-3-kooderille on seuraava.
| INPUTS | TUOTTEET | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Looginen lauseke A2:lle, A1:lle ja A0:lle.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
Edellä mainitut kaksi Boolen funktiota A2, A1 ja A0 voidaan toteuttaa käyttämällä neljää tuloa TAI portit .
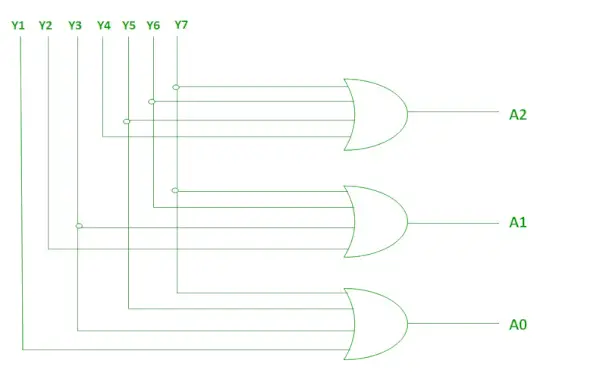
Toteutus OR-portin avulla
Desimaalista BCD-enkooderiin
Desimaalista binääriin kooderi koostuu yleensä 10 syöttölinjaa ja 4 lähtölinjaa . Jokainen tulorivi vastaa jokaista desimaalilukua ja 4 lähtöä vastaavat BCD-koodia. Tämä kooderi hyväksyy dekoodatun desimaalidatan tulona ja koodaa sen BCD-lähtöön, joka on käytettävissä lähtölinjoilla. Alla olevassa kuvassa näkyy desimaali-BCD-kooderin logiikkasymboli:
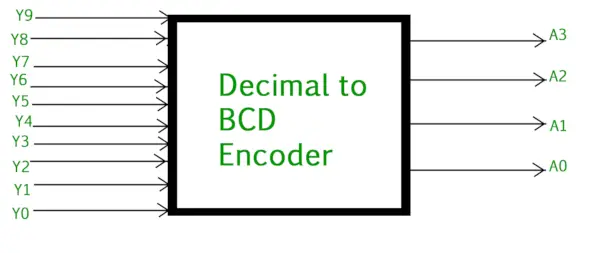
Desimaalista BCD-enkooderiin
Totuustaulukko desimaalista toiseen BCD-kooderi on seuraava.
| INPUTS | TUOTTEET | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Looginen lauseke A3:lle, A2:lle, A1:lle ja A0:lle.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
Edellä mainitut kaksi Boolen funktiota voidaan toteuttaa TAI-porttien avulla.
puun läpikulku
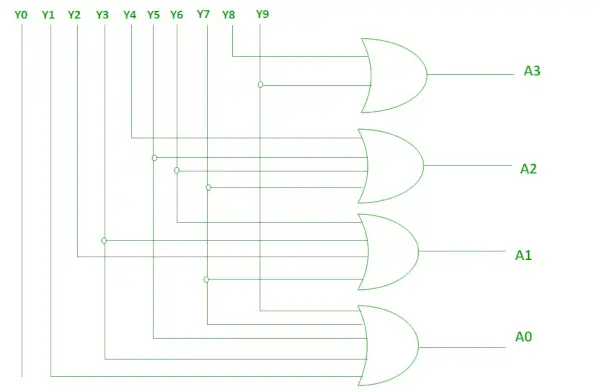
Toteutus OR-portin avulla
Priority Encoder
4-2 prioriteettikooderissa on 4 sisääntuloa : Y3, Y2, Y1 & Y0 ja 2 lähtöä : A1 & A0. Tässä syötteellä Y3 on korkein prioriteetti , kun taas syötteellä Y0 on alin prioriteetti . Tässä tapauksessa, vaikka useampi kuin yksi tulo olisi 1 samanaikaisesti, tulos on (binääri)koodi, joka vastaa tuloa, jolla on korkeampi prioriteetti . Prioriteettikooderin totuustaulukko on seuraava.
java tauko
| INPUTS | TUOTTEET | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | SISÄÄN |
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
A1:n looginen lauseke on esitetty alla.
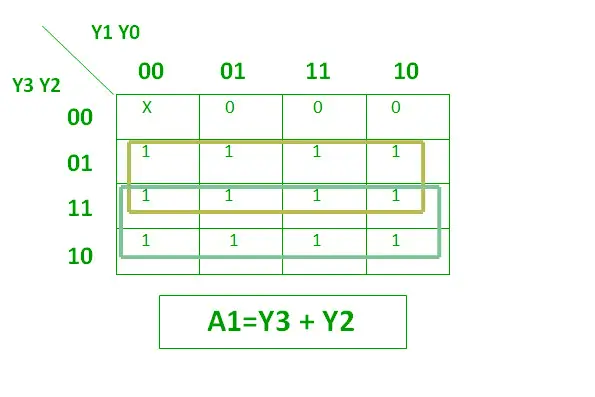
Looginen lauseke
Alla on esitetty A0:n looginen lauseke.
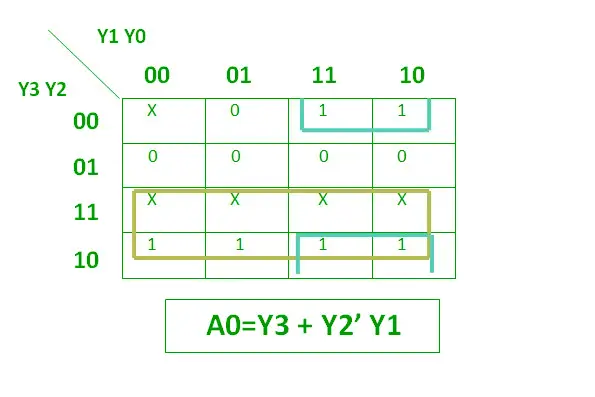
Looginen lauseke
Edellä mainitut kaksi Boolen funktiota voidaan toteuttaa kuten.
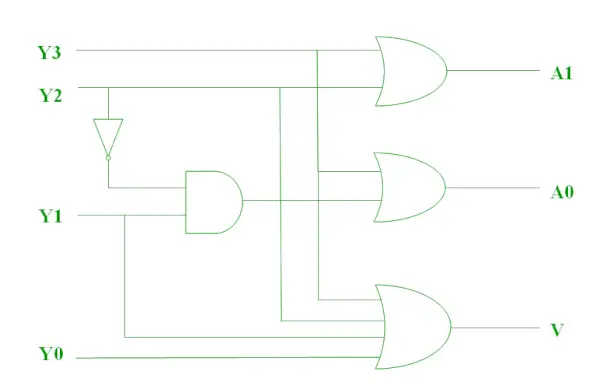
Priority Encoder
Joitakin virheitä, joita yleensä tapahtuu Enkoodereissa, on mainittu alla.
- On epäselvyyttä, kun kaikki kooderin lähdöt ovat nolla.
- Jos useampi kuin yksi tulo on aktiivinen High, kooderi tuottaa lähdön, joka ei välttämättä ole oikea koodi.
Joten näiden vaikeuksien voittamiseksi meidän tulisi asettaa prioriteetit kooderin jokaiselle sisääntulolle. Sitten kooderin ulostulo on koodi, joka vastaa aktiivisia korkea-tuloja, joilla on korkeampi prioriteetti.
Enkooderien sovellus
- Enkooderit ovat hyvin yleisiä elektronisia piirejä, joita käytetään kaikissa digitaalisissa järjestelmissä.
- Enkoodeja käytetään desimaaliarvojen muuntamiseen binääriarvoiksi binääritoimintojen, kuten yhteen-, vähennys- ja kertolaskujen, suorittamiseksi.
- Muita sovelluksia, erityisesti Priority Enkooderien, voivat sisältää keskeytysten havaitsemisen mikroprosessorisovelluksissa.
Enkooderien käytön edut digitaalisessa logiikassa
- Rivien lukumäärän vähentäminen: Enkooderit vähentävät tarvittavien linjojen määrää tiedon siirtämiseen useista tuloista yhteen lähtöön, mikä voi yksinkertaistaa järjestelmän suunnittelua ja vähentää komponenttien kustannuksia.
- Parempi luotettavuus: Muuntamalla useita tuloja yhdeksi sarjakoodiksi kooderit voivat vähentää virheiden mahdollisuutta tiedonsiirrossa.
- Parannettu suorituskyky: Enkooderit voivat parantaa digitaalisen järjestelmän suorituskykyä vähentämällä aikaa, joka tarvitaan tiedon lähettämiseen useista tuloista yhteen lähtöön.
Enkooderien käytön haitat digitaalisessa logiikassa
- Lisääntynyt monimutkaisuus: Enkooderit ovat tyypillisesti monimutkaisempia piirejä verrattuna multiplekserit , ja niiden käyttöönotto edellyttää lisäkomponentteja.
- Rajoitettu tiettyihin sovelluksiin: Enkooderit soveltuvat vain sovelluksiin, joissa rinnakkaiset tulot on muutettava sarjakoodiksi.
- Rajoitettu joustavuus: Enkooderien joustavuus on rajallinen, koska ne voivat koodata vain kiinteän määrän tuloja kiinteään määrään lähtöjä.
- Yhteenvetona voidaan todeta, että kooderit ovat hyödyllisiä digitaalisia piirejä, joilla on etunsa ja haittansa. Valinta, käytetäänkö kooderia vai ei, riippuu järjestelmän erityisvaatimuksista ja monimutkaisuuden, luotettavuuden, suorituskyvyn ja kustannusten välisistä kompromisseista.
GATE CS Corner kysymyksiä
Seuraavien kysymysten harjoitteleminen auttaa sinua testaamaan tietosi. Kaikki kysymykset on esitetty GATEssa aiempina vuosina tai GATE Mock Tests -testeissä. On erittäin suositeltavaa harjoitella niitä.
- GATE CS 2013, kysymys 65
- GATE CS 2014 (sarja 3), kysymys 65
