Oikeassa maailmassa koneoppiminen sovelluksissa on yleistä, että niissä on monia olennaisia ominaisuuksia, mutta vain osa niistä voi olla havaittavissa. Käsiteltäessä muuttujia, jotka ovat joskus havaittavissa ja joskus ei, on todellakin mahdollista hyödyntää tapauksia, joissa muuttuja on näkyvissä tai havaittavissa, jotta voidaan oppia ja tehdä ennusteita tapauksista, joissa se ei ole havaittavissa. Tätä lähestymistapaa kutsutaan usein puuttuvien tietojen käsittelemiseksi. Käyttämällä saatavilla olevia tapauksia, joissa muuttuja on havaittavissa, koneoppimisalgoritmit voivat oppia malleja ja suhteita havaitusta tiedosta. Näitä opittuja malleja voidaan sitten käyttää muuttujan arvojen ennustamiseen tapauksissa, joissa se puuttuu tai ei ole havaittavissa.
Odotus-Maksimointialgoritmilla voidaan käsitellä tilanteita, joissa muuttujat ovat osittain havaittavissa. Kun tietyt muuttujat ovat havaittavissa, voimme käyttää niitä oppiaksemme ja arvioidaksemme niiden arvot. Sitten voimme ennustaa näiden muuttujien arvot tapauksissa, joissa se ei ole havaittavissa.
EM-algoritmi ehdotettiin ja nimettiin vuonna 1977 julkaisemassa peruspaperissa, jonka julkaisivat Arthur Dempster, Nan Laird ja Donald Rubin. Heidän työnsä formalisoi algoritmin ja osoitti sen hyödyllisyyden tilastollisessa mallintamisessa ja arvioinnissa.
EM-algoritmi soveltuu piileviin muuttujiin, jotka ovat muuttujia, jotka eivät ole suoraan havainnoitavissa, mutta jotka päätellään muiden havaittujen muuttujien arvoista. Hyödyntämällä tunnettua yleistä todennäköisyysjakauman muotoa, joka hallitsee näitä piileviä muuttujia, EM-algoritmi voi ennustaa niiden arvot.
EM-algoritmi toimii perustana monille valvomattomille klusterointialgoritmeille koneoppimisen alalla. Se tarjoaa puitteet tilastollisen mallin paikallisten maksimitodennäköisyysparametrien löytämiseksi ja piilevien muuttujien päättelemiseksi tapauksissa, joissa tiedot puuttuvat tai ovat epätäydellisiä.
Odotuksen maksimointialgoritmi (EM).
EM-algoritmi (Expectation-Maximization) on iteratiivinen optimointimenetelmä, joka yhdistää erilaisia valvomattomia koneoppiminen algoritmeja löytääkseen suurimman todennäköisyyden tai suurimman posterioriarvion parametreistä tilastollisissa malleissa, jotka sisältävät havaitsemattomia piileviä muuttujia. EM-algoritmia käytetään yleisesti piilevän muuttujan malleissa ja se pystyy käsittelemään puuttuvia tietoja. Se koostuu estimointivaiheesta (E-vaihe) ja maksimointivaiheesta (M-vaihe), jotka muodostavat iteratiivisen prosessin mallin sovituksen parantamiseksi.
- E-vaiheessa algoritmi laskee piilevät muuttujat eli log-todennäköisyyden odotuksen nykyisten parametriestimaattien avulla.
- M-vaiheessa algoritmi määrittää parametrit, jotka maksimoivat E-vaiheessa saadun odotetun log-todennäköisyyden, ja vastaavat malliparametrit päivitetään arvioitujen latenttien muuttujien perusteella.

Odotus-maksimointi EM-algoritmissa
Toistamalla näitä vaiheita iteratiivisesti EM-algoritmi pyrkii maksimoimaan havaitun datan todennäköisyyden. Sitä käytetään yleisesti ohjaamattomiin oppimistehtäviin, kuten klusterointiin, jossa päätellään piileviä muuttujia, ja sillä on sovelluksia eri aloilla, mukaan lukien koneoppiminen, tietokonenäkö ja luonnollisen kielen käsittely.
Tärkeimmät termit odotusten maksimointialgoritmissa (EM).
Jotkut Odotuksen maksimointialgoritmin (EM) yleisimmin käytetyistä avaintermeistä ovat seuraavat:
- Piilevät muuttujat: Piilevät muuttujat ovat tilastollisissa malleissa havaitsemattomia muuttujia, jotka voidaan päätellä vain epäsuorasti niiden vaikutusten perusteella havaittavissa oleviin muuttujiin. Niitä ei voida mitata suoraan, mutta ne voidaan havaita niiden vaikutuksesta havaittaviin muuttujiin. Todennäköisyys: Se on todennäköisyys havaita annettu data mallin parametreilla. EM-algoritmissa tavoitteena on löytää parametrit, jotka maksimoivat todennäköisyyden. Log-Todennäköisyys: Se on todennäköisyysfunktion logaritmi, joka mittaa havaitun datan ja mallin välisen yhteensopivuuden. EM-algoritmi pyrkii maksimoimaan log-todennäköisyyden. Maksimaalisen todennäköisyyden arviointi (MLE) : MLE on menetelmä tilastollisen mallin parametrien arvioimiseksi etsimällä parametriarvot, jotka maksimoivat todennäköisyysfunktion, joka mittaa kuinka hyvin malli selittää havaitut tiedot. Posteriorinen todennäköisyys: Bayesin päättelyn yhteydessä EM-algoritmia voidaan laajentaa arvioimaan maksimi a posteriori (MAP) -estimaatit, jossa parametrien posteriorinen todennäköisyys lasketaan aiemman jakauman ja todennäköisyysfunktion perusteella. Odotusvaihe (E) : EM-algoritmin E-vaihe laskee piilevien muuttujien odotetun arvon tai posteriorisen todennäköisyyden havaitun datan ja nykyisten parametrien arvioiden perusteella. Se sisältää kunkin piilevän muuttujan todennäköisyyksien laskemisen kullekin datapisteelle. Maksimointivaihe (M) : EM-algoritmin M-vaihe päivittää parametriestimaatit maksimoimalla E-vaiheesta saadun odotetun log-todennäköisyyden. Se sisältää parametriarvojen etsimisen, jotka optimoivat todennäköisyysfunktion, tyypillisesti numeeristen optimointimenetelmien avulla. Konvergenssi: Konvergenssi viittaa tilaan, jossa EM-algoritmi on saavuttanut vakaan ratkaisun. Se määritetään tyypillisesti tarkistamalla, putoaako muutos log-todennäköisyydessä tai parametriarvioissa ennalta määritellyn kynnyksen alapuolelle.
Miten odotusten maksimointialgoritmi (EM) toimii:
Odotus-maksimointialgoritmin ydin on käyttää tietojoukon saatavilla olevaa havaittua dataa puuttuvan datan estimoimiseen ja käyttää sitä sitten parametrien arvojen päivittämiseen. Ymmärretään EM-algoritmi yksityiskohtaisesti.

EM-algoritmin vuokaavio
- Alustus:
- Aluksi otetaan huomioon joukko parametrien alkuarvoja. Joukko epätäydellistä havaittua dataa annetaan järjestelmälle olettaen, että havaitut tiedot ovat peräisin tietystä mallista.
- Laske kunkin piilevän muuttujan posteriori todennäköisyys tai vastuu havaittujen tietojen ja nykyisten parametrien arvioiden perusteella.
- Arvioi puuttuvat tai epätäydelliset data-arvot käyttämällä nykyisiä parametriarvioita.
- Laske havaittujen tietojen log-todennäköisyys nykyisten parametriestimaattien ja arvioitujen puuttuvien tietojen perusteella.
- Päivitä mallin parametrit maksimoimalla odotetun täydellisen datalokin todennäköisyys, joka saadaan E-vaiheesta.
- Tämä edellyttää yleensä optimointiongelmien ratkaisemista, jotta löydetään parametriarvot, jotka maksimoivat log-todennäköisyyden.
- Käytetty optimointitekniikka riippuu ongelman luonteesta ja käytetystä mallista.
- Tarkista konvergenssi vertaamalla muutosta log-todennäköisyydessä tai parametrien arvoja iteraatioiden välillä.
- Jos muutos on ennalta määritellyn kynnyksen alapuolella, lopeta ja katso algoritmin konvergoivan.
- Muussa tapauksessa palaa E-vaiheeseen ja toista prosessi, kunnes konvergenssi on saavutettu.
Odotusten maksimointialgoritmi Vaiheittainen toteutus
Tuo tarvittavat kirjastot
Python 3
str to int
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
Luo tietojoukko kahdella Gaussin komponentilla
Python 3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
Lähtö :

Tiheyskaavio
alennuskuva
Alusta parametrit
Python 3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Suorita EM-algoritmi
- Iteroi määritetyn määrän aikakausia (tässä tapauksessa 20).
- Jokaisella aikakaudella E-vaihe laskee vastuut (gamma-arvot) arvioimalla kunkin komponentin Gaussin todennäköisyystiheydet ja painottamalla niitä vastaavilla suhteilla.
- M-vaihe päivittää parametrit laskemalla kunkin komponentin painotetun keskiarvon ja keskihajonnan
Python 3
vba
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
rudyard kipling jos selitys
Lähtö :

Epoch vs Log-todennäköisyys
Piirrä lopullinen arvioitu tiheys
Python 3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Lähtö :
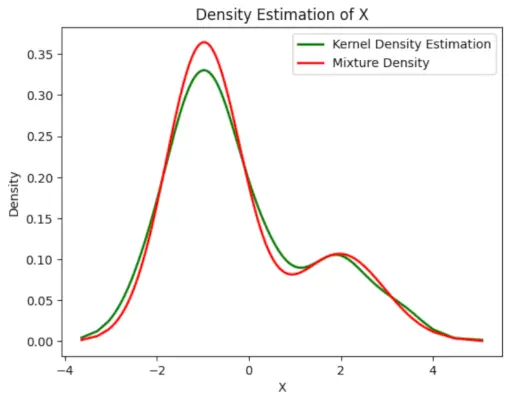
Arvioitu tiheys
Sovellukset EM-algoritmi
- Sitä voidaan käyttää näytteen puuttuvien tietojen täyttämiseen.
- Sitä voidaan käyttää klustereiden ohjaamattoman oppimisen perustana.
- Sitä voidaan käyttää Piilotetun Markovin mallin (HMM) parametrien arvioimiseen.
- Sitä voidaan käyttää latenttien muuttujien arvojen löytämiseen.
EM-algoritmin edut
- On aina taattu, että todennäköisyys kasvaa jokaisella iteraatiolla.
- E-vaihe ja M-vaihe ovat usein melko helppoja moniin toteutuksen ongelmiin.
- M-askeleen ratkaisut ovat usein olemassa suljetussa muodossa.
EM-algoritmin haitat
- Sillä on hidas konvergenssi.
- Se tekee konvergenssin vain paikalliseen optimiin.
- Se vaatii molemmat todennäköisyydet, eteenpäin ja taaksepäin (numeerinen optimointi vaatii vain eteenpäin todennäköisyyden).
