Hitausmomentti on kappaleen ominaisuus pyörivässä liikkeessä. Hitausmomentti on pyörivien kappaleiden ominaisuus, joka pyrkii vastustamaan kappaleen pyörimisliikkeen muutosta. Se on samanlainen kuin minkä tahansa kappaleen inertia translaatioliikkeessä. Matemaattisesti hitausmomentti on kunkin hiukkasen massan ja pyörimisakselin välisen etäisyyden neliön tulon summa. Se mitataan yksikössä kgm 2 .
Opitaan hitausmomentista yksityiskohtaisesti alla olevassa artikkelissa.
Sisällysluettelo
- Inertian hetken määritelmä
- Moment of Inertia Formula
- Hitausmomentiin vaikuttavat tekijät
- Kuinka laskea hitausmomentti?
- Moment of Inertia Formula eri muodoille
- Gyrationin säde
- Hitausmomenttilauseet
- Inertian hetket eri kohteille
Inertian hetken määritelmä
Hitausmomentti on kehon taipumus pyörivässä liikkeessä, joka vastustaa sen muutosta pyörivä liike ulkoisten voimien takia. Hitausmomentti käyttäytyy kulmamassana ja sitä kutsutaan pyörimishitaudeksi. Hitausmomentti on analoginen mekaanisen hitausmomentin kanssa Inertia kehosta.
MOI määritellään suureksi tulon summalla ilmaistuna massa jokaisen hiukkasen pyörimisliikettä suorittavan hiukkasen etäisyyden neliöllä pyörimisakselista.
Hitausmomentin yksikkö
Hitausmomentti on skalaarisuure ja hitausmomentin SI-yksikkö on kgm 2 .
Inertian momentin ulottuvuuskaava
Koska hitausmomentti on annettu massan ja etäisyyden neliön tulona. Sen mittakaava saadaan massan mittakaavan ja pituuden mittakaavan neliön tulona. Hitausmomentin mittakaava on, ML 2
Mikä on Inertia?
Inertia on aineen ominaisuus, jonka ansiosta se pyrkii vastustamaan liiketilan muutosta. Tämä tarkoittaa, että levossa oleva kappale yrittää pysyä levossa ja vastustaa kaikkia voimia, jotka yrittävät saada sen liikkeelle, ja liikkeessä oleva kappale yrittää jatkaa liikettä ja vastustaa kaikkia voimia, jotka yrittävät saada sen muuttamaan liikkeensä suuruutta. Määrällisesti se on yhtä suuri kuin suurin voima, joka yrittää muuttaa sen tilaa liikettä .
Lisätietoja: Inertia .
Moment of Inertia Formula
Hitaushetki on a skalaarinen määrä . Matemaattisesti hiukkasen massan neliön ja etäisyyden pyörimisakselista tuloa kutsutaan hiukkasen hitausmomentiksi pyörimisakselin suhteen.
Yleinen kaava minkä tahansa kohteen hitausmomentin löytämiseksi on,
minä = mr 2
missä,
m on esineen massa'
r on etäisyys pyörimisakselista
Jatkuvista äärettömän pienistä hiukkasista koostuvan kappaleen kohdalla hitausmomentin laskemiseen käytetään hitausmomentin integraalimuotoa.
I = ∫dI
minä =
int_{0}^{M} r^2 dm
Hiukkasjärjestelmän hitausmomentti
Hiukkasjärjestelmän hitausmomentti saadaan kaavalla,
I = ∑m i r i 2
missä,
r i on i:n kohtisuora etäisyysthhiukkanen akselilta
m i on i:n massathhiukkanen
Yllä oleva Hitausmomenttiyhtälö kertoo, että hiukkasjärjestelmän hitausmomentti on yhtä suuri kuin kunkin hiukkasen massan ja kunkin hiukkasen pyörimisakselin etäisyyden neliön tulo.
Alla olevan kuvan osalta
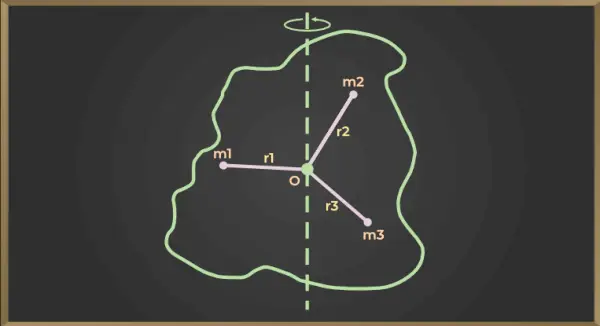
Ensimmäisen hiukkasen hitausmomentti = m1×r12
Toisen hiukkasen hitausmomentti = m2×r22
Kolmannen hiukkasen hitausmomentti = m3×r32
Samalla lailla,
n:n hitausmomenttithhiukkanen = mn×rn2
Nyt koko kehon hitausmomentti pyörimisakselin ympäri AB on yhtä suuri kuin kaikkien hiukkasten hitausmomenttien summa, joten
I = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
java do while esimerkki
I = Σm i ×r i 2
missä,
minä edustavat kappaleen hitausmomenttia pyörimisakselin ympäri
m i on i:n massathhiukkanen,
r i on i:n sädethhiukkanen
S edustaa summaa.
Yhtälöstä voidaan sanoa, että kappaleen hitausmomentti kiinteän akselin ympäri on yhtä suuri kuin kappaleen kunkin hiukkasen massan ja sen kiinteään akseliin nähden kohtisuoran etäisyyden neliön tulo.
Hitausmomentiin vaikuttavat tekijät
Minkä tahansa kohteen hitausmomentti riippuu seuraavista arvoista:
- Esineen muoto ja koko
- Esineen materiaalin tiheys
- Pyörimisakseli
Kuinka laskea hitausmomentti?
Useampaan tapaan on totuttu laske hitausmomentti mistä tahansa pyörivästä esineestä.
- Tasaisten esineiden hitausmomentti lasketaan ottamalla sen massan tulo neliöllä sen etäisyydestä pyörimisakselista (r2).
- Epätasaisille kohteille lasketaan hitausmomentti ottamalla yksittäisten pistemassojen tulon summa kullakin eri säteellä. Tätä varten käytetty kaava on
I = ∑m i r i 2
Moment of Inertia Formula eri muodoille
Tässä taulukossa käsitellään joidenkin symmetristen kohteiden hitausmomentin lausekkeita sekä niiden pyörimisakselia:

| Esine | Akseli | Hitausmomentin ilmaisu |
|---|---|---|
| Ontto sylinteri Ohutseinämäinen | Keski | I = Mr2 |
| Ohut rengas | Halkaisija | I = 1/2 Mr2 |
| Rengas tai ontto sylinteri | Keski | I = 1/2 M(r22+ r12) |
| Kiinteä sylinteri | Keski | I = 1/2 Mr2 |
| Yhtenäinen levy | Halkaisija | I = 1/4 Mr2 |
| Ontto pallo | Keski | I = 2/3 Mr2 |
| Kiinteä pallo | Keski | I = 2/5 Mr2 |
| Yhtenäinen symmetrinen pallomainen kuori | Keski | |
| Tasainen levy tai suorakulmainen rinnakkaisputki | Keski | I = 1/12 M(a2+ b2) |
| Ohut sauva | Keski | I = 1/12 Mr2 |
| Ohut sauva | Rodin päässä | I = 1/3 Mr2 |
Gyrationin säde
The Gyrationin säde kappale määritellään kohtisuoraksi etäisyydeksi pyörimisakselista massapisteeseen, jonka massa on yhtä suuri kuin koko kappaleen massa ja hitausmomentti on yhtä suuri kuin kappaleen todellinen hitausmomentti sellaisena kuin se on ollut. oletetaan, että kehon kokonaismassa on keskittynyt sinne. Se on kuvitteellinen etäisyys. Pyörityksen säde on merkitty K:llä.
Jos kappaleen massa ja pyörimissäde ovat vastaavasti M ja K, niin kappaleen hitausmomentti on
I = MK 2 ……(1)
Siten kappaleen pyörimissäde on kohtisuorassa pyörimisakseliin nähden, jonka neliö kerrottuna kappaleen massalla antaa kappaleen hitausmomentin tuon akselin ympäri.
Jälleen yhtälöllä (1), K2= I/M
K = √(I/m)
Siten kappaleen pyörityksen säde akselin ympäri on yhtä suuri kuin kappaleen tämän akselin suhteen neliöjuuri.
Hitausmomenttilauseet
On olemassa kahden tyyppisiä lauseita, jotka ovat erittäin tärkeitä hitausmomentin kannalta:
- Rinnakkaisakselin lause
- Pystysuoran akselin lause
Pystysuoran akselin lause
Pystysuoran akselin lause toteaa, että kappaleen hitausmomenttien summa kahden keskenään kohtisuoran akselin ympärillä, jotka sijaitsevat kappaleen tasossa, on yhtä suuri kuin kappaleen hitausmomentti kolmannen akselin ympärillä, joka on kohtisuorassa molempiin akseliin nähden ja kulkee niiden pisteen kautta risteyksestä.

Yllä olevassa kuvassa HÄRKÄ ja OY ovat kaksi akselia kappaleen tasossa, jotka ovat kohtisuorassa toisiinsa nähden. Kolmas akseli on OZ joka on kohtisuorassa kappaleen tasoa vastaan ja kulkee kappaleen leikkauspisteen kautta HÄRKÄ ja OY kirveet. Jos minä x , minä ja , ja minä Kanssa ovat kappaleen hitausmomentteja akselin ympäri HÄRKÄ , OY , ja OZ akselit vastaavasti, sitten tämän lauseen mukaan
java tulostus
minä x + minä ja = minä Kanssa
Rinnakkaisakselin lause
Mukaan Rinnakkaisakselin lause , kappaleen hitausmomentti tietyn akselin ympäri on hitausmomentin summa kappaleen massakeskipisteen kautta kulkevan akselin ympärillä ja kappaleen massan neliön ja kappaleen välisen kohtisuoran etäisyyden tulo. kaksi akselia.

Olkoon yllä oleva kuva, meidän on löydettävä hitausmomentti minä O pisteen läpi kulkevasta kehosta O ja tasoon nähden kohtisuoran akselin ympäri, kun taas kappaleen hitausmomentti kulkee massakeskuksen kautta C ja suunnilleen annetun akselin suuntainen akseli on minä C , sitten tämän lauseen mukaan
minä O = minä C + Ml 2
missä
M on koko kehon massa
l on kahden akselin välinen kohtisuora etäisyys.
Inertian hetket eri kohteille
Eri esineiden hitausmomenttia käsitellään alla tässä artikkelissa
Suorakaiteen muotoisen levyn hitausmomentti
Jos levyn massa on M, pituus l ja leveys b, niin hitausmomentti kulkee painopisteen läpi ja levyn tasoon nähden kohtisuoran akselin ympäri.

I = M(l 2 + b 2 / 12)
Levyn hitausmomentti
Jos kiekon massa on M ja säde r, niin hitausmomentti kiekon geometrisen akselin suhteen on

I = 1/2 (Mr 2 )
Tangon hitausmomentti
Jos tangon massa on M ja pituus l, niin hitausmomentti akselin ympäri, joka on kohtisuorassa sauvan pituuteen nähden ja kulkee sen painopisteen kautta

I = ML 2 /12
Ympyrän hitausmomentti
Jos renkaan massa on M ja renkaan säde on r, niin hitausmomentti renkaan keskustaan nähden kohtisuorassa kulkevan akselin ympäri on

I = Mr 2
Pallon hitausmomentti
Jos kiinteän pallon massa on M ja sen säde on r, niin hitausmomentti sen halkaisijan suhteen on

I = 2/5 Mr 2
Kiinteän sylinterin hitausmomentti
Kiinteän sylinterin, jonka säde on 'R' ja massa M, hitausmomentti saadaan kaavalla

I = 1/2MR 2
Onton sylinterin hitausmomentti
Ontolla sylinterillä on kaksi sädettä, nimittäin sisäsäde ja ulkoinen säde. Onton sylinterin hitausmomentti, jonka massa on M, ulkoinen säde R1, ja sisäinen säde R2annetaan muodossa

I = 1/2M (R 1 2 + R 2 2 )
Kiinteän pallon hitausmomentti
Kiinteän massapallon hitausmomentti 'M' ja säde 'R' on annettu

I = 2/5MR 2
Onton pallon hitausmomentti
Onton pallon, jonka massa on M ja säde 'R', hitausmomentti on annettu

I = 2/3MR 2
Sormuksen hitausmomentti
Renkaan hitausmomentti on annettu kahdelle tapaukselle, kun pyörimisakseli kulkee keskipisteen kautta ja kun pyörimisakseli kulkee halkaisijan läpi.
Renkaan hitausmomentti keskustan läpi kulkevan akselin ympäri on annettu
muuntaa merkkijonon int

I = MR 2
Renkaan hitausmomentti halkaisijan läpi kulkevan akselin ympäri on annettu

I = Mr 2 /2
Neliön hitausmomentti
Sivun 'a' neliön hitausmomentti annetaan muodossa

I = a 4 /12
Neliömäisen levyn, jonka sivu on pituus 'l' ja massa M, hitausmomentti on annettu
I = 1/6 ml 2
Kolmion hitausmomentti
Kolmion hitausmomentti on annettu kolmelle tilanteelle, ensin, kun akseli kulkee keskipisteen läpi, toiseksi, kun akseli kulkee kannan läpi ja kolmanneksi, kun akseli on kohtisuorassa kantaan nähden. Katsotaanpa niiden kaava yksitellen. Kolmiolle, jonka kanta on ”b” ja korkeus ”h”, hitausmomentin kaava annetaan seuraavasti

Kun akseli kulkee Centroidin läpi
I = bh 3 /36
Kun akseli kulkee pohjan läpi
I = bh 3 /12
Kun akseli on kohtisuorassa kantaan nähden
I = (hb/36)(b 2 – b 1 b + b 1 2 )
Ero hitausmomentin ja hitausmomentin välillä
Inertian ja hitausmomentin välinen ero on taulukoitu alla:
| Kyllä ei. | Inertia | Hitausmomentti |
|---|---|---|
| 1. | Sen merkitys on lineaarisessa liikkeessä. | Sen merkitys on pyörivässä liikkeessä. |
| 2. | Se on esineen ominaisuus, joka vastustaa objektin tilan muutosta lineaarisessa liikkeessä. | Hitausmomentti on esineen se ominaisuus, joka vastustaa kappaleen tilan muutosta pyörivässä liikkeessä. |
| 3. | Esineen inertia riippuu vain sen massasta. | Esineen hitausmomentti riippuu sen massasta ja sen massajakaumasta suhteessa pyörimisakseliin. |
| 4. | Esineen inertia on kiinteä. | Esineen hitausmomentti vaihtelee eri pyörimisakseleiden mukaan. |
Pyörivän rungon kineettinen energia
Oletetaan kappaletta, jonka massa on 'm', joka pyörii nopeudella v etäisyydellä 'r' pyörimisakselista. Sen kulmanopeus saadaan sitten kaavalla ω = v/r, sitten v = rω. Nyt tiedämme, että Kineettinen energia kehosta on annettu
KE = 1/2 mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2vai niin2
⇒ KE = 1/2Iω 2
Pyörivän kappaleen kineettinen energia saadaan siis puolella hitausmomentin tulosta. kulmanopeus kehosta. Pyörivän kappaleen kineettistä energiaa kutsutaan myös Pyörimisen kineettinen energia . Pyörimiskineettisen energian kaava on annettu seuraavasti
KE = 1/2Iω 2
Hitausmomentti(I) on riippumaton kappaleen kulmanopeudesta. Se on pyörivän kappaleen massan ja kappaleen etäisyyden pyörimisakselista funktio. Näin ollen havaitsemme, että kulmaliike on analoginen lineaarisen liikkeen kanssa, mikä tarkoittaa, että hitausmomentin merkitys on siinä, että se antaa käsityksen siitä, kuinka massat jakautuvat eri etäisyyksille pyörivän kappaleen pyörimisakselista.
Hitausmomentin soveltaminen
Moment of Inertialla on useita sovelluksia, joista osa käsitellään alla:
- Suuremman hitausmomentin ansiosta maa pyörii akselinsa ympäri samalla kulmanopeudella.
- Pieni liikkuva pyörä on sijoitettu lasten leikkimoottorin alle. Kun tätä pyörää on hierottu maahan ja poistuttu moottorista, pyörän hitausmomentista johtuen moottori pysyy käynnissä jonkin aikaa.
- Jokainen moottori koostuu suuresta ja raskaasta pyörästä, joka on kiinnitetty sen akseliin, ja suurin osa sen massasta on sen kehällä. Siksi sen hitausmomentti on suuri. Tätä pyörää kutsutaan vauhtipyöräksi. Moottorin akselia käyttävä vääntömomentti kasvaa jatkuvasti. Siksi akselin pyöriminen ei välttämättä ole tasaista, mutta liikkuvan pyörän, jolla on suurempi inertia, läsnäolo, akseli jatkaa pyörimistä lähes tasaisella nopeudella.
- Härkäkärryjen, riksojen, skootterien, polkupyörien jne. pyörässä suurin osa massasta on keskittynyt sen ympyrään tai vanteeseen. tämä vanne tai rutiini on kiinnitetty pyörän akseliin jäykillä pinnoilla. Näin toimimalla sen hitausmomentti kasvaa. Siksi, kun jalat lakkaavat liikkumasta pyöräilyn aikana, pyörä jatkaa pyörimistä jonkin aikaa.
Myös Tarkista
- Pyörivän liikkeen kinematiikka
- Jäykän kehon liike
- Rolling Motion
Ratkaistiin esimerkkejä hitausmomenteista
Esimerkki 1: 500 g painava kappale pyörii akselin ympäri. kappaleen massakeskipisteen etäisyys pyörimisakselista on 1,2 m. löytää kappaleen hitausmomentti pyörimisakselin ympäri.
Ratkaisu:
Ottaen huomioon, että M = 500 g = 0,5 kg, r = 1,2 m.
On selvää, että koko kehon massa voidaan olettaa olevan sen massakeskipisteessä. Sitten kappaleen hitausmomentti pyörimisakselin ympäri.
I = Mr2
I = 0,5 × (1,2)2
I = 0,72 kg m2
Esimerkki 2: Kierrossäde 12 cm:n päässä 1,2 kg painavan kappaleen massakeskipisteestä olevan akselin ympäri on 13 cm. Laske Kierrossäde ja hitausmomentti massakeskuksen läpi kulkevan akselin ympäri.
Ratkaisu:
Ottaen huomioon, että M = 1,0 kg, K = 13 cm, l = 12 cm, KCM=?, minäCM= ?
Rinnakkaisakselin lauseesta I = ICM+ Ml2
K2= KCM2+ l2
tai KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Nyt, hitausmomentti ICM= MKCM2
minäCM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
Esimerkki 3: 0,1 kg painava kappale pyörii akselin ympäri. jos kappaleen massakeskipisteen etäisyys pyörimisakselista on 0,5 m, niin etsi kappaleen hitausmomentti.
Ratkaisu:
Ottaen huomioon, että M = 0,1 kg ja r = 0,5 m
joten minä = Mr2
I = 0,1 × (0,5)2
tostring-menetelmä javassaI = 0,025 kg m2
Esimerkki 4: Renkaiden hitausmomentti sen keskipisteen kautta kohtisuorassa pyöreän renkaan tasoon nähden kulkevan akselin ympäri on 200 gm cm 2 . Mikä on sen halkaisijan hitausmomentti?
Ratkaisu:
Pyöreän renkaan hitausmomentti akselin ympärillä, joka kulkee toisen sen tasoon nähden kohtisuorassa olevan keskipisteen kautta
HERRA2= 200 gm cm2
Hitausmomentti lähestyy halkaisijaa
= 1/2 MR2
= 1/2 × 200 = 100 gm cm2
Usein kysytyt kysymykset hitausmomenteista
Kuinka hitausmomentti lasketaan?
Peruskaava minkä tahansa yhtenäisen esineen hitausmomentin löytämiseksi on,
minä = mr 2
missä,
m on esineen massa'
r on etäisyys pyörimisakselista
Kuinka laskea säteen hitausmomentti?
Säteen hitausmomentti keskustaa pitkin ja siihen nähden vaakasuora akseli lasketaan kaavalla,
I = ML 2 / 12
Mistä kehon hitausmomentti riippuu?
Minkä tahansa kohteen hitausmomentti riippuu alla olevista tekijöistä:
- ruumiin massa,
- Pyörimisakseli
- Esineen muoto ja koko
Mikä on hitausmomentin yksikkö?
Hitausmomentin yksikkö on Kgm 2
Voiko hitausmomentti olla negatiivinen?
Ei, hitausmomentti ei voi koskaan olla negatiivinen.
Mikä on massan hitausmomentti?
Massahitausmomentti on kehon vastuksen mittaus sen kulmamomentin tai -suunnan muutoksille. Pistemassan massan hitausmomentti saadaan kaavalla I = mr2ja hiukkassysteemille massan hitausmomentti annetaan muodossa I = Σimiri2
Mikä on alueen hitausmomentti?
Area Moment of Inertia on 2D-muototason ominaisuus, joka näyttää kuinka pisteet ovat hajallaan suhteessa mielivaltaiseen akseliin tasossa. Alueen hitausmomentti tunnetaan myös alueen toisena hetkenä tai alueen neliömomenttina. Alueen hitausmomentin kaava xy-tasossa on annettu muodossa Ixy= ∫xy dxdxy = ∫xy dA
