Luokittelijan suorituskykyä voidaan arvioida useilla tavoilla. Tässä artikkelissa esittelemme Precision-Recall Curve -käyrän ja tutkimme tarkemmin kahden suositun suorituskyvyn raportointimenetelmän eroa: Tarkkuus-palautuskäyrä (PR) ja Vastaanottimen toimintaominaisuus (ROC) Käyrä. ROC-käyrästä on jo keskusteltu artikla . Ymmärrämme lyhyesti, mikä on tarkkuus-palautuskäyrä.
Mitä on tarkkuus ja muistaminen?
Tarkkuus
- Oikein ennustettujen positiivisten havaintojen suhdetta kaikkiin ennustettuihin positiivisiin havaintoihin kutsutaan tarkkuudella.
- Se mittaa, kuinka hyvin malli ennustaa myönteisiä tuloksia.
- Tarkkuuskaava on:
- Tarkkuus liittyy positiivisten ennusteiden laatuun. Suuri tarkkuus osoittaa, että mallissa on alhainen väärien positiivisten tulosten määrä.
Palauttaa mieleen
- Oikein ennustettujen positiivisten havaintojen suhdetta todellisten positiivisten havaintojen kokonaismäärään kutsutaan muistutukseksi.
- Se mittaa, kuinka hyvin malli voi kaapata kunkin asiaankuuluvan ilmentymän.
- Palautus lasketaan tällä kaavalla:
- Recall koskee mallin kaapamien asiaankuuluvien esiintymien määrää. Korkea palautus osoittaa, että mallissa on alhainen väärien negatiivisten tulosten määrä.
Empiirisen tulkinnan kannalta sekavuusmatriisi, jossa on neljä olennaista termiä, on hyödyllisin työkalu tarkkuuden ja muistamisen ymmärtämiseen:
- True Positive (TP): positiivisten luokkaesiintymien määrä, jotka tunnistetaan tarkasti
- Väärä positiivinen (FP): Virheellisesti positiivisiksi luokkaesiintymiksi tunnistettujen negatiivisten luokkailmentymien lukumäärä tunnetaan nimellä Väärä positiivinen (FP).
- True Negative (TN): Negatiivisten luokan esiintymien määrä, jotka tunnistetaan tarkasti
- Väärä negatiivinen (FN): Niiden positiivisten luokkaesiintymien määrä, jotka luokitellaan vahingossa negatiivisiksi luokkaesiintymiksi (False Negative tai FN)
Precision-Recall (PR) -käyrä koneoppimisessa
Tarkkuus on osuus oikea positiiviset luokitukset (tosi positiivinen) jaettuna kokonaismäärällä ennustettu tehdyt positiiviset luokitukset (tosi positiivinen + väärä positiivinen). Palauttaa mieleen on osuus oikea positiiviset luokitukset (tosi positiivinen) jaettuna luokitusten kokonaismäärällä todella positiiviset luokitukset (tosi positiivinen + väärä negatiivinen).
PR-käyrä on yksinkertaisesti kaavio, jossa on tarkkuusarvot y-akselilla ja Recall-arvot x-akselilla. Toisin sanoen PR-käyrä sisältää
- On tärkeää huomata, että tarkkuutta kutsutaan myös positiiviseksi ennakoivaksi arvoksi (PPV).
- Palautusta kutsutaan myös herkkyydeksi, osumasuhteeksi tai todelliseksi positiiviseksi prosentiksi (TPR).
Alla oleva kuva esittää näytteen PR- ja ROC-käyrien vertailun. 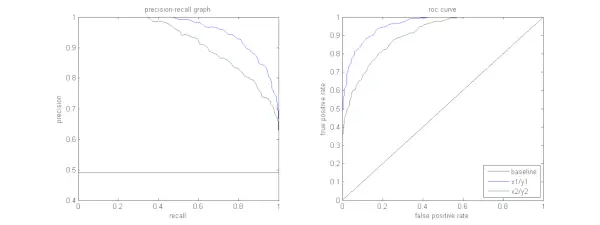
Tarkkuus-palautuskäyrän tulkitseminen
On toivottavaa, että algoritmilla on sekä suuri tarkkuus että korkea palautus. Useimmat koneoppimisalgoritmit sisältävät kuitenkin usein kompromissin näiden kahden välillä. Hyvällä PR-käyrällä on suurempi AUC (käyrän alla oleva pinta-ala) . Yllä olevassa kuvassa sinistä viivaa vastaava luokitin toimii paremmin kuin vihreää viivaa vastaava luokitin. On tärkeää huomata, että luokitin, jonka AUC on korkeampi ROC-käyrä on aina korkeampi AUC myös PR-käyrällä. Harkitse algoritmia, joka luokittelee, kuuluuko asiakirja luokkaan Urheiluuutiset. Oletetaan, että on 12 dokumenttia, joissa on seuraavat perustotuus (todellinen) ja luokittimen lähtöluokkatunnisteet.
| Asiakirjan tunnus | Perustotuus | Luokittimen lähtö |
|---|---|---|
| D1 | Urheilu | Urheilu |
| D2 | Urheilu | Urheilu |
| D3 | Ei urheilua | Urheilu |
| D4 | Urheilu | Ei urheilua |
| D5 | Ei urheilua | Ei urheilua |
| D6 | Urheilu | Ei urheilua |
| D7 | Ei urheilua | Urheilu |
| D8 | Ei urheilua | Ei urheilua |
| D9 | Ei urheilua | Ei urheilua |
| D10 | Urheilu | Urheilu |
| D11 | Urheilu | Urheilu |
| D12 | Urheilu | Ei urheilua |
Etsitään nyt TP-, TN-, FP- ja FN-arvot.
Käytämme esimerkkiä, joka sisältää urheilu- tai ei urheiluluokituksen asiakirjoja selittääksemme paremmin todellisten positiivisten (TP), todellisten negatiivisten (TN), väärien positiivisten (FP) ja väärien negatiivisten (FN) määritelmiä luokittelun yhteydessä:
Todelliset positiiviset (TP): Asiakirjat, jotka luokiteltiin tarkasti urheiluksi ja jotka itse asiassa koskivat urheilua. Asiakirjat D1, D2, D10 ja D11 tässä skenaariossa ovat TP:n esiintymiä.
Todelliset negatiiviset (TN): Todelliset negatiivit ovat tapauksia, joissa asiakirja oli asianmukaisesti merkitty Ei urheilua, vaikka sillä ei ollut mitään tekemistä urheilun kanssa. Tässä tapauksessa TN osoitetaan asiakirjoilla D5, D8 ja D9.
Väärät positiiviset (FP): Asiakirjat, jotka on virheellisesti luokiteltu urheiluksi, vaikka niillä ei ollut mitään tekemistä urheilun kanssa. Tässä on joitain FP-esimerkkejä, asiakirjoja D3 ja D7.
Väärät negatiivit (FN): Esimerkkejä asiakirjoista, jotka on virheellisesti merkitty Ei urheiluksi, mutta todellisuudessa ne koskivat urheilua. Asiakirjat D4, D6 ja D12 ovat tässä tapauksessa FN-esimerkkejä.
Kun otetaan huomioon nämä luvut: Kaupunki =4, TN =3, FP =2, FN =3
Lopuksi tarkkuus ja palautus lasketaan seuraavasti:
Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}
Recall = frac{TP}{TP+FN} = frac{4}{7} Tästä seuraa, että poisto on 4/7, kun tarkkuus on 2/3. Toisin sanoen kaikista tapauksista, joiden odotettiin olevan positiivisia, kaksi kolmasosaa oli tarkasti luokiteltu (tarkkuus), ja kaikista tapauksista, jotka olivat todella positiivisia, malli pystyi kaappaamaan niistä neljä seitsemäsosaa (muistaa).
Asettamalla erilaisia kynnysarvoja saamme useita tällaisia tarkkuus-, palautuspareja. Piirtämällä useita sellaisia P-R-pareja, joiden jompikumpi arvo vaihtelee välillä 0-1, saamme PR-käyrän.
Tarvitsetko PR-käyrän, kun ROC-käyrä on olemassa?
PR-käyrä on erityisen hyödyllinen tiedonhaun tulosten raportoinnissa.
Tiedonhaussa etsitään asiakirjoja tietyn käyttäjän kyselyn kannalta olennaisten asiakirjojen löytämiseksi. Oletetaan esimerkiksi, että käyttäjä kirjoittaa hakulausekkeen Pink Elephants. Hakukone selaa miljoonia asiakirjoja (joitakin optimoituja algoritmeja käyttämällä) löytääkseen kourallisen asiaankuuluvia asiakirjoja. Siksi voimme turvallisesti olettaa, että ei. asiaankuuluvien asiakirjojen määrä on paljon vähemmän kuin nro. ei-olennaisista asiakirjoista.
Tässä skenaariossa
- TP = relevanttien haettujen asiakirjojen lukumäärä (hyvät tulokset).
- FP = haettujen asiakirjojen määrä, jotka eivät ole asiaankuuluvia (väärähakutulokset).
- TN = Hakemattomien asiakirjojen lukumäärä, jotka eivät ole relevantteja.
- FN = Noudattamattomien asiakirjojen lukumäärä (hyviä asiakirjoja emme löytäneet).
ROC-käyrä on käyrä, joka sisältää Recall = TPR =
java-koodaus if else-lauseessa
Lisäksi FPR ei auta meitä arvioimaan hakujärjestelmää hyvin, koska haluamme keskittyä enemmän haettuihin asiakirjoihin, ei noutamattomiin asiakirjoihin. PR-käyrä auttaa ratkaisemaan tämän ongelman. PR-käyrällä on palautusarvo (TPR) x-akselilla ja tarkkuus =
Milloin käyttää ROC vs. Precision-Recall käyriä?
ROC (Receiver Operating Characteristic) -käyrät ovat sopivia, kun luokkajakauma on tasapainoinen, ja väärillä positiivisilla ja väärillä negatiivisilla seurauksilla on samanlaiset seuraukset. Ne kuvaavat herkkyyden ja spesifisyyden välistä kompromissia. Sitä vastoin Precision-Recall-käyrät ovat parempia, kun käsitellään epätasapainoisia tietojoukkoja, ja niissä keskitytään positiiviseen luokkaennusteen suorituskykyyn.
Precision-Recall tarjoaa käsityksen mallin kyvystä luokitella positiiviset esiintymät oikein. Valinta ROC:n ja Precision-Recallin välillä riippuu ongelman erityistarpeista, mikä korostaa tiedon jakautumisen ja erityyppisten virheiden seurausten ymmärtämisen tärkeyttä.
Tarkkuus-palautuskäyrän peruskoodin toteutus
Tarvittavien kirjastojen tuonti
Nämä koodirivit tuovat Python-kirjastot ja moduulit, joita tarvitaan luomaan tarkkuus-palautuskäyrä sci-kit-learn ja visualisoida tulokset Matplotlib . Matplotlib on suosittu Python-piirtokirjasto, ja pyplot tarjoaa suoraviivaisen käyttöliittymän erilaisten kaavioiden ja kaavioiden luomiseen. Logistinen regressio on suosittu luokitusalgoritmi binääri- ja moniluokkaluokitustehtäviin. Tarkkuus-palautuskäyrä ja AUC ovat suosittuja arviointimittareita binääriluokitus ongelmia, erityisesti käsiteltäessä epätasapainoisia tietojoukkoja.
Python 3 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc> Tietojoukko käytetty
Tämä koodi luo synteettisen tietojoukon binääristä luokitusongelmaa varten käyttämällä sci-kit-learnin make_classification-funktiota.
Python 3 # Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)> Harjoittele ja koe Split
The train_test_split scikit-learnin toimintoa käytetään tässä koodinpätkässä jakamaan aiemmin luotu synteettinen tietojoukko (X ja y) koulutus- ja testausjoukkoihin. Tämä jako on kriittinen vaihe koneoppimismallien arvioinnissa. Mallia opetetaan X_train- ja y_train-datan perusteella, ennen kuin se testataan X_test- ja y_test-tiedoilla, jotta nähdään, kuinka hyvin se toimii näkymättömissä näytteissä. Train_test_split-funktio erottaa harjoitus- ja testausjoukot ja varmistaa, että mallin suorituskyky kuvastaa sen yleistämistä uuteen, ennen näkemättömään dataan.
Python 3 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)> Mallirakennus
Tässä käytämme logistista regressiota mallin harjoittamiseen harjoitustietojoukossa. Suosittu binääriluokittelualgoritmi, logistinen regressio, on toteutettu sci-kit-learn-luokassa LogisticRegression.
Python 3 # Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)> Mallin ennustus
Nämä laskelmat antavat yleensä tarkkuus- ja palautusarvot eri päätöskynnyksille, joiden avulla voit piirtää tarkkuus-palautuskäyrän tai tutkia tarkkuuden ja muistamisen suhteellista merkitystä eri ajankohtina. Ja laskemalla Käyrän alla oleva alue (AUC) tarkkuus-palautuskäyrälle.
Python 3 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)> PR-käyrän piirtäminen
Tämä koodilohko tarjoaa vakiomenetelmän tarkkuus-palautuskäyrän visualisointiin ja antaa sinun arvioida tarkkuuden ja palauttamisen välisen kompromissin eri päätöskynnyksillä. Mallin kokonaissuorituskyky tarkkuus-palautuskäyrällä on yhteenveto selityksessä näkyvällä AUC-pisteellä.
Python 3 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()> Lähtö :

Tarkkuus-palautuskäyrä
Usein kysytyt kysymykset (FAQ)
K. Mitä tarkkuus on?
Tarkasti ennustettujen positiivisten havaintojen suhdetta ennustettujen positiivisten havaintojen kokonaismäärään kutsutaan tarkkuudella. Se mittaa, kuinka hyvin malli ennustaa myönteisiä tuloksia. Seuraava on tarkkuuskaava:
Precision = frac{True Positives}{True Positives + False Positives}
K. Mikä on Recall?
Recall on oikein ennustettujen positiivisten havaintojen suhde todellisten positiivisten havaintojen kokonaismäärään. Sitä kutsutaan myös herkkyydeksi tai todelliseksi positiiviseksi koroksi. Se arvioi, kuinka hyvin malli voi kaapata kunkin asiaankuuluvan tapauksen. Palautus lasketaan seuraavalla kaavalla:
Precision = frac{True Positives}{True Positives + False Negatives}
K. Miksi tarvitsemme tarkkuutta ja muistamista?
Luokittelijan suorituskyvyn arvioimiseksi binääri- ja moniluokkaluokitusongelmissa käytetään kahta arviointimetriikkaa: tarkkuus ja muistaminen. Positiivisen ennusteen tarkkuus mitataan tarkkuudella ja positiivisen ennusteen täydellisyys mitataan palauttamalla.
K. Mikä on takaisinkutsumisen ja tarkkuuden välinen kompromissi?
Muistaminen ja tarkkuus ovat usein kompromisseja. Muistaminen voi kärsiä tarkkuuden kasvaessa ja päinvastoin. Tämä kompromissi voidaan hallita muuttamalla palkkia positiivisen esiintymän tunnistamiseksi. Päinvastoin, matalampi kynnys johtaa pienempään palauttamiseen, mutta korkeampaan tarkkuuteen. Päätös palauttamisen ja tarkkuuden välillä perustuu tietyn ongelman yksityiskohtiin.
K. Mikä on F1-pistemäärä ja miten se liittyy tarkkuuteen ja muistamiseen?
Muistamisen ja tarkkuuden harmoninen keskiarvo tunnetaan F1-pisteenä. Se tarjoaa oikeudenmukaisen mittauksen, joka ottaa huomioon sekä väärät positiiviset että väärät negatiiviset. F1-pisteet lasketaan seuraavalla kaavalla:
F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall} F1-pisteet ovat erityisen hyödyllisiä, kun tarkkuus ja muistaminen ovat epätasapainossa ja halutaan tasapainottaa näiden kahden välillä.
merkkijono java indexof
