Logistinen regressio on valvottu koneoppimisalgoritmi käytetty luokittelutehtävät jossa tavoitteena on ennustaa todennäköisyys, että ilmentymä kuuluu tiettyyn luokkaan vai ei. Logistinen regressio on tilastollinen algoritmi, joka analysoi kahden datatekijän välistä suhdetta. Artikkelissa tarkastellaan logistisen regression perusteita, sen tyyppejä ja toteutuksia.

Sisällysluettelo

• Mikä on logistinen regressio?
• Logistinen toiminto – Sigmoid-toiminto
• Logistisen regression tyypit
• Logistisen regression oletukset
• Miten logistinen regressio toimii?
• Logistisen regression koodin käyttöönotto
• Tarkkuus-palautuksen kompromissi logistisen regression kynnysasetuksessa
• Kuinka arvioida logistinen regressiomalli?
• Erot lineaarisen ja logistisen regression välillä

Mikä on logistinen regressio?

Logistista regressiota käytetään binäärissä luokittelu missä käytämme sigmoiditoiminto , joka ottaa syötteen itsenäisinä muuttujina ja tuottaa todennäköisyysarvon välillä 0 ja 1.

Esimerkiksi meillä on kaksi luokkaa Luokka 0 ja luokka 1, jos syötteen logistisen funktion arvo on suurempi kuin 0,5 (kynnysarvo), niin se kuuluu luokkaan 1, muuten se kuuluu luokkaan 0. Sitä kutsutaan regressioksi, koska se on laajennus lineaarinen regressio mutta sitä käytetään pääasiassa luokitteluongelmiin.

Avainkohdat:

• Logistinen regressio ennustaa kategorisen riippuvan muuttujan tuoton. Siksi tuloksen on oltava kategorinen tai erillinen arvo.
• Se voi olla joko Kyllä tai Ei, 0 tai 1, tosi tai epätosi jne., mutta sen sijaan, että se antaisi tarkan arvon 0 ja 1, se antaa todennäköisyysarvot, jotka ovat välillä 0 ja 1.
• Logistisessa regressiossa sovitetaan regressioviivan sijaan S:n muotoinen logistinen funktio, joka ennustaa kaksi maksimiarvoa (0 tai 1).

Logistinen toiminto – Sigmoid-toiminto

• Sigmoidifunktio on matemaattinen funktio, jota käytetään kartoittaa ennustetut arvot todennäköisyyksiksi.
• Se kuvaa minkä tahansa todellisen arvon toiseksi arvoksi välillä 0 ja 1. Logistisen regression arvon tulee olla välillä 0 - 1, mikä ei voi ylittää tätä rajaa, joten se muodostaa S-muodon kaltaisen käyrän.
• S-muotoista käyrää kutsutaan sigmoidifunktioksi tai logistiseksi funktioksi.
• Logistisessa regressiossa käytämme kynnysarvon käsitettä, joka määrittelee joko 0:n tai 1:n todennäköisyyden. Esimerkiksi kynnysarvon ylittävät arvot pyrkivät 1:een ja kynnysarvojen alapuolella olevat arvot yleensä 0:aan.

Logistisen regression tyypit

Luokkien perusteella logistinen regressio voidaan jakaa kolmeen tyyppiin:

1. Binomi: Binomiaalisessa logistisessa regressiossa voi olla vain kaksi mahdollista riippuvaisten muuttujien tyyppiä, kuten 0 tai 1, Hyväksytty tai Hylätty jne.
2. Moninomi: Moninomisessa logistisessa regressiossa voi olla 3 tai useampia mahdollisia järjestämättömiä riippuvaisen muuttujan tyyppejä, kuten kissa, koira tai lammas
3. Tavallinen: Ordinaalisessa logistisessa regressiossa voi olla 3 tai useampia mahdollisia järjestetyn tyyppisiä riippuvia muuttujia, kuten matala, keskitaso tai korkea.

Logistisen regression oletukset

Tutkimme logistisen regression oletuksia, koska näiden oletusten ymmärtäminen on tärkeää, jotta voimme varmistaa, että käytämme mallin asianmukaista sovellusta. Oletukseen sisältyy:

1. Riippumattomat havainnot: Jokainen havainto on riippumaton toisistaan. mikä tarkoittaa, että minkään syöttömuuttujan välillä ei ole korrelaatiota.
2. Binääririippuvaiset muuttujat: Oletetaan, että riippuvaisen muuttujan on oltava binäärinen tai kaksijakoinen, mikä tarkoittaa, että sillä voi olla vain kaksi arvoa. Useampaan kuin kahteen kategoriaan käytetään SoftMax-toimintoja.
3. Riippumattomien muuttujien ja logaritmisten kertoimien välinen lineaarisuussuhde: Riippumattomien muuttujien ja riippuvan muuttujan logaritmisten välisen suhteen tulee olla lineaarinen.
4. Ei poikkeavia: Tietojoukossa ei saa olla poikkeavuuksia.
5. Suuri otoskoko: Otoskoko on riittävän suuri

Logistiseen regressioon liittyvät terminologiat

Tässä on joitain yleisiä termejä, jotka liittyvät logistiseen regressioon:

• Riippumattomat muuttujat: Syöttöominaisuudet tai ennustajatekijät, joita sovelletaan riippuvaisen muuttujan ennusteisiin.
• Riippuva muuttuja: Logistisen regressiomallin tavoitemuuttuja, jota yritämme ennustaa.
• Logistinen toiminto: Kaava, jota käytetään kuvaamaan, kuinka riippumattomat ja riippuvat muuttujat liittyvät toisiinsa. Logistinen funktio muuntaa syötemuuttujat todennäköisyysarvoiksi välillä 0 ja 1, mikä edustaa todennäköisyyttä, että riippuva muuttuja on 1 tai 0.
• Kertoimet: Se on jonkin tapahtuvan suhde johonkin, joka ei tapahdu. se eroaa todennäköisyydestä, koska todennäköisyys on jonkin tapahtuman suhde kaikkeen, mitä mahdollisesti voi tapahtua.
• Log-kertoimet: Log-odds, joka tunnetaan myös nimellä logit-funktio, on kertoimien luonnollinen logaritmi. Logistisessa regressiossa riippuvan muuttujan logaritmit mallinnetaan riippumattomien muuttujien ja leikkauspisteen lineaarisena yhdistelmänä.
• Kerroin: Logistisen regressiomallin estimoidut parametrit osoittavat, kuinka riippumattomat ja riippuvat muuttujat liittyvät toisiinsa.
• Siepata: Logistisen regressiomallin vakiotermi, joka edustaa logaritmistimiä, kun kaikki riippumattomat muuttujat ovat nolla.
• Maksimitodennäköisyysarvio : Logistisen regressiomallin kertoimien estimointiin käytetty menetelmä, joka maksimoi mallin antamien tietojen havainnoinnin todennäköisyyden.

Miten logistinen regressio toimii?

Logistinen regressiomalli muuttaa lineaarinen regressio funktio jatkuvan arvon ulostulo kategoriseksi arvoksi käyttämällä sigmoidifunktiota, joka kuvaa minkä tahansa syötetyn riippumattomien muuttujien reaaliarvoisen joukon arvoksi välillä 0 ja 1. Tämä funktio tunnetaan logistiikkafunktiona.

ohjelma javassa

Olkoon itsenäiset tuloominaisuudet:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

ja riippuva muuttuja on Y, jolla on vain binääriarvo, eli 0 tai 1.

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

Käytä sitten monilineaarista funktiota syötemuuttujiin X.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

Tässäx_i on X:n i:s havainto,w_i = [w_1, w_2, w_3, cdots,w_m] on painot tai kerroin, ja b on harhatermi, joka tunnetaan myös nimellä leikkaus. yksinkertaisesti tämä voidaan esittää painon ja harhan pistetulona.

z = wcdot X +b

mistä keskustelimme edellä on lineaarinen regressio .

Sigmoiditoiminto

Nyt käytämme sigmoiditoiminto jossa syöte on z ja löydämme todennäköisyyden välillä 0 ja 1. eli ennustettu y.

sigma(z) = frac{1}{1-e^{-z}}

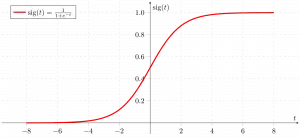
Sigmoid-toiminto

Kuten yllä on esitetty, kuvion sigmoidifunktio muuntaa jatkuvan muuttujan datan todennäköisyys eli välillä 0 ja 1.

• sigma(z) suuntautuu kohti 1 asz ightarrowinfty
• sigma(z) suuntautuu kohti 0 asz ightarrow-infty
• sigma(z) on aina rajoittunut välillä 0 ja 1

jossa todennäköisyys olla luokka voidaan mitata seuraavasti:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Logistinen regressioyhtälö

Pariton on jonkin tapahtuman suhde johonkin, joka ei tapahdu. se eroaa todennäköisyydestä, koska todennäköisyys on jonkin tapahtuman suhde kaikkeen, mitä mahdollisesti voi tapahtua. niin outoa olisi:

frac{p(x)}{1-p(x)} = e^z

Luonnollisen lokin käyttäminen parittomalla. sitten log odd on:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

niin lopullinen logistinen regressioyhtälö on:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Logistisen regression todennäköisyysfunktio

Ennustetut todennäköisyydet ovat:

• jos y=1 Ennustetut todennäköisyydet ovat: p(X;b,w) = p(x)
• jos y = 0 Ennustetut todennäköisyydet ovat: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

Otetaan luonnonhirsiä molemmilta puolilta

smtp Internet-protokolla

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Log-likelihood-funktion gradientti

Suurimman todennäköisyyden arvioiden löytämiseksi erottelemme w.r.t w,

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Logistisen regression koodin käyttöönotto

Binomiaalinen logistinen regressio:

Kohdemuuttujalla voi olla vain 2 mahdollista tyyppiä: 0 tai 1, jotka voivat edustaa voitto vs tappio, hylätty vs epäonnistuminen, kuollut vs elossa jne., tässä tapauksessa käytetään sigmoidifunktioita, joista on jo keskusteltu edellä.

Tarvittavien kirjastojen tuonti mallivaatimuksen perusteella. Tämä Python-koodi näyttää, kuinka rintasyöpätietoaineistoa käytetään logistisen regressiomallin toteuttamiseen luokittelua varten.

Lähtö :

Logistisen regressiomallin tarkkuus (%): 95,6140350877193

Multinomiaalinen logistinen regressio:

Kohdemuuttujalla voi olla 3 tai useampia mahdollisia tyyppejä, joita ei ole järjestetty (eli tyypeillä ei ole kvantitatiivista merkitystä), kuten sairaus A vs. tauti B vs. tauti C.

Tässä tapauksessa softmax-funktiota käytetään sigmoidifunktion sijasta. Softmax-toiminto K-luokille tulee:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

Tässä, K edustaa elementtien lukumäärää vektorissa z, ja i, j iteroituu kaikkien vektorin elementtien yli.

Silloin luokan c todennäköisyys on:

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

Multinomial Logistic Regressionissa lähtömuuttujalla voi olla enemmän kuin kaksi mahdollista erillistä lähtöä . Harkitse numerotietojoukkoa.

Lähtö:

Logistisen regressiomallin tarkkuus (%): 96,52294853963839

Kuinka arvioida logistinen regressiomalli?

Voimme arvioida logistisen regressiomallin seuraavilla mittareilla:

• Tarkkuus: Tarkkuus antaa oikein luokiteltujen tapausten osuuden.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• Tarkkuus: Tarkkuus keskittyy positiivisten ennusteiden tarkkuuteen.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Muista (herkkyys tai todellinen positiivinen prosentti): Palauttaa mieleen mittaa oikein ennustettujen positiivisten tapausten osuutta kaikista todellisista positiivisista tapauksista.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• F1-pisteet: F1-pisteet on tarkkuuden ja muistamisen harmoninen keskiarvo.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Vastaanottimen toimintakäyrän alla oleva alue (AUC-ROC): ROC-käyrä kuvaa todellisen positiivisen määrän suhteessa vääriin positiivisiin prosenttiosuuksiin eri kynnyksillä. AUC-ROC mittaa tämän käyrän alla olevaa pinta-alaa ja tarjoaa kokonaismitan mallin suorituskyvystä eri luokituskynnysten yli.
• Tarkkuus-palautuskäyrän alla oleva alue (AUC-PR): Samanlainen kuin AUC-ROC, AUC-PR mittaa tarkkuus-palautuskäyrän alla olevaa aluetta ja tarjoaa yhteenvedon mallin suorituskyvystä eri tarkkuuden palauttamisen kompromisseissa.

Tarkkuus-palautuksen kompromissi logistisen regression kynnysasetuksessa

Logistisesta regressiosta tulee luokittelutekniikka vasta, kun päätöskynnys tuodaan kuvaan. Kynnysarvon asettaminen on erittäin tärkeä näkökohta logistisessa regressiossa ja riippuu itse luokitteluongelmasta.

Kynnysarvon arvopäätökseen vaikuttavat suuresti arvot tarkkuutta ja muistamista. Ihannetapauksessa haluamme sekä tarkkuuden että muistamisen olevan 1, mutta näin on harvoin.

Tapauksessa a Precision-Recall kompromissi , käytämme seuraavia argumentteja kynnyksen määrittämiseen:

1. Matala tarkkuus / korkea palautus: Sovelluksissa, joissa haluamme vähentää väärien negatiivien määrää vähentämättä välttämättä väärien positiivisten määrää, valitsemme päätösarvon, jolla on pieni Tarkkuus- tai korkea Recall-arvo. Esimerkiksi syöpädiagnoosisovelluksessa emme halua, että yksikään sairastunut potilas luokitellaan sairaamattomaksi ottamatta huomioon, jos potilaalla on virheellisesti diagnosoitu syöpä. Tämä johtuu siitä, että syövän puuttuminen voidaan havaita muilla lääketieteellisillä sairauksilla, mutta taudin esiintymistä ei voida havaita jo hylätyssä ehdokkaassa.
2. Suuri tarkkuus / alhainen palautus: Sovelluksissa, joissa haluamme vähentää väärien positiivisten määrää vähentämättä välttämättä väärien negatiivien määrää, valitsemme päätösarvon, jolla on korkea Precision-arvo tai alhainen Recall-arvo. Jos esimerkiksi luokittelemme asiakkaita, reagoivatko he positiivisesti vai negatiivisesti personoituun mainokseen, haluamme olla täysin varmoja, että asiakas reagoi mainokseen positiivisesti, koska muuten negatiivinen reaktio voi aiheuttaa potentiaalisen myynnin menetystä asiakas.

Erot lineaarisen ja logistisen regression välillä

Ero lineaarisen regression ja logistisen regression välillä on se, että lineaarisen regression tulos on jatkuva arvo, joka voi olla mikä tahansa, kun taas logistinen regressio ennustaa todennäköisyyden, kuuluuko esiintymä tiettyyn luokkaan vai ei.

Logistinen regressio – Usein kysytyt kysymykset (FAQ)

Mitä on logistinen regressio koneoppimisessa?

Logistinen regressio on tilastollinen menetelmä kehittää koneoppimismalleja, joissa on binääririippuvaisia ​​muuttujia, eli binäärisiä. Logistinen regressio on tilastollinen tekniikka, jota käytetään kuvaamaan tietoja ja yhden riippuvan muuttujan ja yhden tai useamman riippumattoman muuttujan välistä suhdetta.

Mitkä ovat kolme logistisen regression tyyppiä?

Logistinen regressio luokitellaan kolmeen tyyppiin: binääri, multinomi ja järjestysluku. Ne eroavat sekä toteutuksen että teorian osalta. Binääriregressiolla on kaksi mahdollista lopputulosta: kyllä ​​tai ei. Multinomiaalista logistista regressiota käytetään, kun arvoja on kolme tai useampia.

arraylist

Miksi luokitusongelmassa käytetään logistista regressiota?

Logistinen regressio on helpompi toteuttaa, tulkita ja kouluttaa. Se luokittelee tuntemattomat tietueet hyvin nopeasti. Kun tietojoukko on lineaarisesti erotettavissa, se toimii hyvin. Mallin kertoimet voidaan tulkita ominaisuuden tärkeyden indikaattoreiksi.

Mikä erottaa logistisen regression lineaarisesta regressiosta?

Lineaarista regressiota käytetään ennustamaan jatkuvia tuloksia, kun taas logistista regressiota käytetään ennustamaan todennäköisyyttä, että havainto kuuluu tiettyyn luokkaan. Logistic Regression käyttää S-muotoista logistista funktiota kartoittamaan ennustetut arvot välillä 0 ja 1.

Mikä rooli logistiikkatoiminnolla on logistisessa regressiossa?

Logistinen regressio perustuu logistiseen funktioon, joka muuntaa tuotoksen todennäköisyyspisteiksi. Tämä pistemäärä edustaa todennäköisyyttä, että havainto kuuluu tiettyyn luokkaan. S-muotoinen käyrä auttaa tietojen kynnysmäärittelyssä ja luokittelussa binäärituloksiin.