Trigonometria on tärkeä matematiikan haara, joka käsittelee suorakulmaisen kolmion kulmien ja sivujen pituuden välistä suhdetta. Kuusi trigonometristä suhdetta tai funktiota ovat sini, kosini, tangentti, kosekantti ja sekantti, ja trigonometrinen suhde on suorakulmaisen kolmion sivujen välinen suhde. Sini-, kosini- ja tangenttifunktiot ovat kolme tärkeää trigonometristä funktiota, koska muut kolme, eli kosekantti-, sekantti- ja kotangenttifunktiot ovat sini-, kosini- ja tangenttifunktioiden käänteisfunktioita.
- sin θ = Vastakkainen puoli/hypotenuusa
- cos θ = Viereinen puoli/Hypotenuusa
- tan θ = vastakkainen puoli / viereinen puoli
- cosec θ = hypotenuusa/vastakkainen puoli
- sec θ = Hypotenuusa/viereinen puoli
- pinnasänky θ = Viereinen puoli/vastakkainen puoli
Tangenttifunktio on yksi kuudesta trigonometrisesta funktiosta, joita käytetään trigonometrian kaavat .
Sisällysluettelo
Tangentin kaava
Kulman tangentti suorakulmaisessa kolmiossa on vastakkaisen sivun pituuden ja viereisen sivun pituuden suhde annettuun kulmaan. Kirjoitamme tangentin funktion tan. Tarkastellaan suorakulmaista kolmiota XYZ ja yksi sen teräväkulmaisista kulmista on θ. Vastakkainen puoli on sivu, joka on vastakkainen kulman θ kanssa ja viereinen sivu on sivu, joka on kulman θ vieressä.
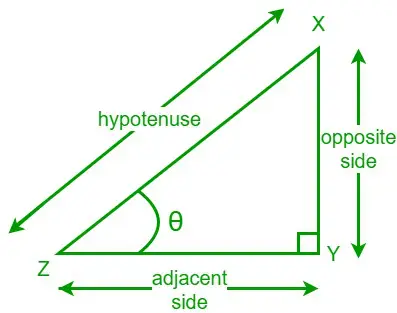
Nyt annetun kulman θ tangenttikaava on,
tan θ = vastakkainen puoli / viereinen puoli
Jotkut tangenttien peruskaavat
Tangenttifunktio kvadranteissa
Tangenttifunktio on positiivinen ensimmäisessä ja kolmannessa kvadrantissa ja negatiivinen toisessa ja neljännessä neljänneksessä.
- tan (2π + θ) = tan θ (1stkvadrantti)
- tan (π – θ) = – tan θ (2ndkvadrantti)
- tan (π + θ) = tan θ (3rdkvadrantti)
- tan (2π – θ) = – tan θ (4thkvadrantti)
Tangenttifunktio negatiivisena funktiona
Tangenttifunktio on negatiivinen funktio, koska negatiivisen kulman tangentti on tangentin positiivisen kulman negatiivinen.
tan (-θ) = – tan θ
Tangenttifunktio sini- ja kosinifunktiona
Tangenttifunktio sini- ja kosinifunktioiden suhteen voidaan kirjoittaa seuraavasti,
tan θ = sin θ/cos θ
Tiedämme, että tan θ = vastakkainen puoli / viereinen puoli
Jaa nyt sekä osoittaja että nimittäjä hypotenuusalla
tan θ = (vastakkainen puoli/hypotenuusa)/(viereinen puoli/hypotenuusa)
Tiedämme, että sin θ = vastakkainen puoli/hypotenuusa
cos θ = viereinen sivu/hypotenuusa
Näin ollen tan θ = sin θ/cos θ
Tangenttifunktio sinifunktion kannalta
Tangenttifunktio sinifunktiona voidaan kirjoittaa seuraavasti,
tan θ = sin θ/(√1 – sin 2 i)
Tiedämme sen,
tan θ = sin θ/cos θ
kuinka monta kaupunkia on yhdysvalloissa
Pythagoralaisista identiteeteistä meillä on
ilman2θ + cos2θ = 1
cos2θ = 1 – synti2i
cos θ = √(1 – sin2i)
Näin ollen tan θ = sin θ/(√1 – sin2i)
Tangenttifunktio kosinifunktiona
Tangenttifunktio kosinifunktiona voidaan kirjoittaa seuraavasti,
tan θ = (√1 -cos 2 i)/cos i
Tiedämme sen,
tan θ = sin θ/cos θ
Pythagoralaisista identiteeteistä meillä on
ilman2θ + cos2θ = 1
ilman2θ = 1 – cos2i
sin θ = √(1 – cos2i)
Näin ollen tan θ = (√1 – cos2i)/cos i
Tangenttifunktio kotangenttifunktion kannalta
Tangenttifunktio kotangenttifunktion suhteen voidaan kirjoittaa seuraavasti,
tan θ = 1/vauvansänky θ
tai
tan θ = pinnasänky (90° – θ) (tai) pinnasänky (π/2 – θ)
Tangenttifunktio kosekanttifunktion kannalta
Tangenttifunktio kosekanttifunktiona voidaan kirjoittaa seuraavasti,
tan θ = 1/√(kosek 2 minä - 1)
Pythagoralaisista identiteeteistä meillä on
cosec2θ – pinnasänky2θ = 1
pinnasänky2θ = kosek2minä - 1
pinnasänky θ = √(kosek2minä - 1)
Tiedämme sen,
tan θ = 1/vauvansänky θ
Näin ollen tan θ = 1/√(kosek2minä - 1)
Tangenttifunktio sekanttifunktion kannalta
Sekanttifunktion tangenttifunktio voidaan kirjoittaa seuraavasti,
tan θ = √s 2 minä - 1
Pythagoralaisista identiteeteistä meillä on
sek2θ – niin2θ = 1
tan θ = sek2minä - 1
Näin ollen tan θ = √(s2minä - 1)
Tangenttifunktio kaksoiskulman kannalta
Kaksoiskulman tangenttifunktio on,
tan 2θ = (2 tan θ)/(1 – tan 2 i)
Tangenttifunktio kolmoiskulman suhteen
Kolmoiskulman tangenttifunktio on,
tan 3θ = (3 tan θ – tan 3 θ) / (1-3 tan 2 i)
Tangenttifunktio puolikulman suhteen
Puolikulman tangenttifunktio on,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Tangenttifunktio kahden kulman yhteen- ja vähennyslaskussa
Tangenttifunktion summa- ja erotuskaavat ovat,
rusketus (A + B) = (rusketus A + rusketus B)/(1 – rusketus A rusketus B)
rusketus (A – B) = (rusketus A – rusketus B)/(1 + rusketus A rusketus B)
Trigonometrinen suhdetaulukko
| Kulma (asteina) | Kulma (radiaaneina) | synti i | cos θ | tan θ = sin θ/cos θ | cosec θ | sek θ | pinnasänky i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Määrittelemätön | 1 | Määrittelemätön |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 ensimmäisen asteen logiikka | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = määrittelemätön | 1 | Määrittelemätön | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | (23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Määrittelemätön | -1 | Määrittelemätön |
Ratkaistu esimerkki tangenttikaavoista
Esimerkki 1: Etsi tan θ:n arvo, jos sin θ = 2/5 ja θ on ensimmäinen kvadranttikulma.
Ratkaisu:
Annettu,
- sin θ = 2/5
Pythagoralaisesta identiteetistä, joka meillä on,
ilman2θ + cos2θ = 1
cos2θ = 1 – synti2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Koska θ on ensimmäinen kvadranttikulma, cos θ on positiivinen.
jframecos θ = √21/5
Tiedämme sen,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21/21
Joten tan θ:n arvo, kun sin θ = 2/5 ja θ on ensimmäisessä kvadrantissa, on (2√21) /(21)
Esimerkki 2: Etsi tan x:n arvo, jos sec x = 13/12 ja x on neljäs kvadranttikulma.
Ratkaisu:
Annettu, sek x = 13/12
Pythagoralaisista identiteeteistä meillä on
sek2x - niin2x = 1
niin2x = sek2x – 1= (13/12)2- 1
niin2x = (169/144) – 1 = 25/144
rusketus x = ± 5/12
Koska x on neljäs kvadranttikulma, tan x on negatiivinen.
rusketus x = – 5/12
Siten, rusketus x = – 5/12
Esimerkki 3: Jos tan X = 2/3 ja tan Y = 1/2, mikä on tan (X + Y) arvo?
Ratkaisu:
Annettu,
tan X = 2/3 ja tan Y = 1/2
Tiedämme sen,
rusketus (X + Y) = (rusketus X + rusketus Y)/(1 – rusketus x rusketus Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3) × (1/2)]
= (7/6)/(2/3) = 7/4
Siten, tan(X + Y) = 7/4
Esimerkki 4: Laske tangenttifunktio, jos suorakulmaisen kolmion viereiset ja vastakkaiset sivut ovat 4 cm ja 7 cm.
Ratkaisu:
Annettu,
Vierekkäinen sivu = 4 cm
Vastakkainen puoli = 7 cm
Tiedämme sen,
tan θ = vastakkainen puoli / viereinen puoli
tan θ = 7/4 = 1,75
Siten, tan θ = 1,75
Esimerkki 5: Mies katsoo kellotornia 60° kulmassa tornin huipulle, jonka korkeus on 100 m. Mikä on miehen ja tornin jalan välinen etäisyys?
Ratkaisu:
Annettu,
Tornin korkeus = 100 m ja θ = 60°
Olkoon ihmisen ja tornin jalan välinen etäisyys = d
Meillä on,
tan θ = vastakkainen puoli / viereinen puoli
rusketus 60° = 100/d
√3 = 100/pv [Koska, joten 60° = √3]
d = 100/√3
Siksi miehen ja tornin jalan välinen etäisyys on 100/√3
Esimerkki 6: Etsi tan θ:n arvo, jos sin θ = 7/25 ja sec θ = 25/24.
Ratkaisu:
Annettu,
sin θ = 7/25
sek θ = 25/24
Tiedämme sen,
sek θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Meillä on,
tan θ = sin θ/cos θ
= (25/7)/(24/25)
= 7/24
Siten, tan θ = 7/24
Esimerkki 7: Etsi tan θ:n arvo, jos cosec θ = 5/3 ja θ on ensimmäinen kvadranttikulma.
Ratkaisu:
Annettu, cosec θ = 5/3
Pythagoralaisista identiteeteistä meillä on
kokoelmat javassacosec2θ – pinnasänky2θ = 1
pinnasänky2θ = kosek2minä - 1
pinnasänky θ = (5/3)2– 1 = (25/9) – 1 = 16/9
pinnasänky θ = ±√16/9 = ± 4/3
Koska θ on ensimmäinen kvadranttikulma, sekä kotangentti- että tangenttifunktiot ovat positiivisia.
pinnasänky θ = 4/3
Tiedämme sen,
pinnasänky θ = 1/tan θ
4/3 = 1/tanθ
tan θ = 3/4
Siten, tan θ = 3/4
Esimerkki 8: Etsi tan 3θ, jos sin θ = 3/7 ja θ on ensimmäinen kvadranttikulma.
Ratkaisu :
Annettu, sin θ = 12/13
Pythagoralaisesta identiteetistä, joka meillä on,
ilman2θ + cos2θ = 1
cos2θ = 1 – synti2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Koska θ on ensimmäinen kvadranttikulma, cos θ on positiivinen.
cos θ = 5/13
Tiedämme sen,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Näin ollen tan θ = 12/5
Nyt tiedämme, että
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

