Matematiikan puolisuunnikas: Trapetsi on monikulmio, jossa on neljä sivua, eli se on nelikulmio. Trapezium on peräisin kreikan sanasta trapeze, joka tarkoittaa pöytää. Se on monimutkainen nelikulmio. Trapetsi on erityinen nelikulmio, jossa on vain yksi pari yhdensuuntaisia sivuja. Trapetsi on kaksiulotteinen muoto, joka näkyy taulukona.
Trapetsilla on neljä sivua ja neljä kärkeä. Näemme puolisuunnikkaan muodon jokapäiväisessä elämässämme ja se on yksi yleisimmistä muodoista. Tässä artikkelissa opimme mikä on trapetsi matematiikassa, sen ominaisuudet, kaavat, esimerkit ja puolisuunnikkaan tyypit sekä joitakin siitä ratkaistuja esimerkkejä.
Sisällysluettelo
- Mikä on trapetsi matematiikassa?
- Trapetsiumtyypit
- Epäsäännöllinen trapetsi
- Trapeziumin ominaisuudet
- Trapezium-kaava
- Trapezium Formulan alue
- Trapezium-kaavan ympärysmitta
- Ero trapetsion ja puolisuunnikkaan välillä
- Puolisuunnikkaan kulmat
- Trapetsion diagonaali
- Esimerkkejä trapetsiumista
Mikä on trapetsi matematiikassa?
Puolisuunnikas on suljetun muotoinen kaksiulotteinen nelikulmio, jossa on pari yhdensuuntaisia vastakkaisia sivuja. Puolisuunnikkaan yhdensuuntaisia sivuja kutsutaan kantaviksi ja ei-rinnakkaisia puolisuunnikkaan jaloiksi. Trapetsissa on neljä sivua ja neljä kulmaa. A suunnikas kutsutaan myös puolisuunnikkaaksi, jossa on kaksi yhdensuuntaista sivua.
Trapetsium määritelmä
Puolisuunnikas on nelikulmio (nelisivuinen monikulmio), jossa on vähintään yksi pari yhdensuuntaisia sivuja. Näitä yhdensuuntaisia sivuja kutsutaan puolisuunnikkaan pohjaksi, ja kahta muuta sivua kutsutaan jaloiksi, jotka eivät välttämättä ole yhdensuuntaisia.
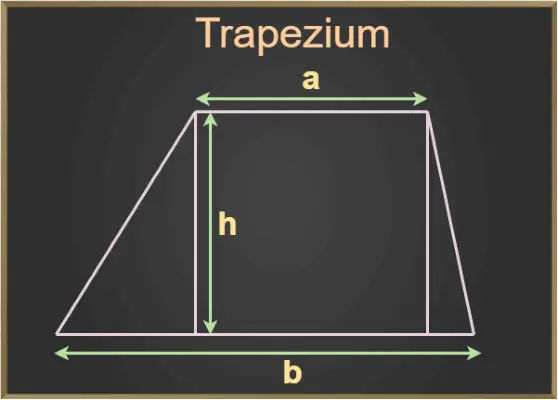
Yllä olevassa kuvassa a ja b ovat puolisuunnikkaan kantat ja h on puolisuunnikkaan korkeus.
Trapetsiummuoto
Trapetsium on a nelikulmio eli monikulmio, jossa on neljä sivua. Puolisuunnikkaan on neljä sivua ja pari vastakkaista sivua, jotka ovat yhdensuuntaisia toistensa kanssa. Puolisuunnikkaan muoto on hyvin yleinen, ja näemme jokapäiväisessä elämässämme erilaisia asioita, jotka ovat samanlaisia kuin puolisuunnikkaan. Joitakin tosielämän esimerkkejä havaitsemistamme puolisuunnikkaasta ovat puolisuunnikkaan muotoiset pöydät, laatat, maalaukset ja muut.
Trapetsiumtyypit
Sivujen ja kulmien perusteella trapetsi on kolmen tyyppistä:
- Scalene Trapezium
- Tasakylkinen puolisuunnikas
- Oikea trapetsi

Tasakylkinen puolisuunnikas
Puolisuunnikasta, jonka jalat ovat yhtä pitkät, kutsutaan tasakylkiseksi puolisuunnikkaaksi, eli tasakylkisessä puolisuunnikkaan kaksi ei-rinnakkaista sivua ovat yhtä suuret.
Scalene Trapezium
Puolisuunnikkaan, jonka kaikki sivut eivät ole yhtä suuria, kutsutaan skaala-trapetsiksi. Scalene-trapetsiumissa ei ole kahta samanarvoista kulmaa.
Oikea trapezium
Puolisuunnikas, jossa on suorakulmapari vierekkäin, tunnetaan suorana puolisuunnikkaana.
Epäsäännöllinen trapetsi
Trapetsissa on yksi pari yhdensuuntaisia sivuja ja kaksi muuta sivua eivät ole yhdensuuntaisia. Säännöllisessä puolisuunnikkaan kaksi muuta ei-samansuuntaista sivua ovat yhtä suuret, mutta epäsäännöllisen puolisuunnikkaan kaksi ei-rinnakkaista vastakkaista sivua ovat eriarvoisia.
Trapeziumin ominaisuudet
Trapetsilla on useita ominaisuuksia, joista jotkut ovat seuraavat:
- Rinnakkaiset sivut: Puolisuunnikkaan kaksi yhdensuuntaista sivua, joita kutsutaan kantaviksi. Esimerkki: Sivut AB ja CD ovat yhdensuuntaiset toistensa kanssa, kuten kuvassa.
- Ei-rinnakkaiset sivut: Puolisuunnikkaan ei-samansuuntaisia sivuja kutsutaan jaloiksi ja puolisuunnikkaan jalat eivät ole yhtä pitkiä. Esimerkki: Sivut AD ja BC ovat puolisuunnikkaan ei-rinnakkaiset sivut.
- Korkeus tai korkeus: Pohjien välistä kohtisuoraa etäisyyttä kutsutaan puolisuunnikkaan korkeudeksi tai korkeudeksi. Yllä olevassa kaaviossa h on puolisuunnikkaan korkeus.
- Kulmien summa
- Vierekkäiset sisäkulmat puolisuunnikasessa summautuvat 180°:een. Esimerkki: Sisäkulmia on kaksi paria. Yksi pari on ∠ A ja ∠ D, kun taas toinen pari on ∠ B ja ∠ C. Kunkin sisäkulmien yhteiskulmaparin summa on 180°.
- Puolisuunnikkaan sisäkulmien summa on aina 360°. Esimerkki : Kuvassa ∠A+∠D on 180° ja ∠B+∠C on 180°. Siksi ∠A+∠D +∠B+∠C = 360°.
- Mediaani: Puolisuunnikkaan mediaani on jana, joka yhdistää jalkojen keskipisteet. Mediaani on yhdensuuntainen kantaan nähden ja sen pituus on kantajen pituuksien keskiarvo.
- Puolisuunnikkaan on täsmälleen yksi pari vastakkaisia sivuja, jotka ovat yhdensuuntaisia.
Trapezium-kaava
Tärkeitä trapeziumin kaavoja ovat:
- Trapeziumin alue = ½ (rinnakkaisten sivujen summa) × (rinnakkaisten sivujen välinen etäisyys)
- Puolisuunnikkaan kehä = Kaikkien neljän puolen summa
Trapezium Formulan alue
Puolisuunnikkaan kaksi yhdensuuntaista sivua a ja b yksikköä vastaavasti, ja sen korkeus on h.
Nyt puolisuunnikkaan pinta-ala voidaan laskea etsimällä emästen keskiarvo ja kertomalla sen tulos korkeudella. Siten,
Trapeziumin alue = ((a +b)/2) × h
missä,
- a ja b ovat Trapeziumin tukikohtia
- h on Korkeus
Isosceles trapezium -alue
Olkoot a ja b puolisuunnikkaan ABCD yhdensuuntaisten sivujen pituus, missä a ja b ovat puolisuunnikkaan kantat ja a>b.
Nyt, koska se on tasakylkinen puolisuunnikas, c on molempien ei-rinnakkaisten sivujen pituus ja h on puolisuunnikkaan korkeus.
Nyt AB = a, CD = b, BC = AD = c
Sisään Suorakulmainen kolmio , AED
kohtisuoran pituus, h = √(c 2 – (a–b) 2 ) [käyttäen Pythagoraan lause ]….(1)
Nyt,
Pinta-ala = ½ × yhdensuuntaisten sivujen summa × puolisuunnikkaan korkeus
Pinta-ala = ½ × (a+b) × h
Käyttämällä yhtälöä (1)
java arraylist
Isosceles trapezium -alue = 1/2 × [√(c 2 – (a-b) 2 ) (a+b)]
Trapezium-kaavan ympärysmitta
Puolisuunnikkaan ympärysmitta saadaan laskemalla sen kaikkien sivujen summa. Siten,
Puolisuunnikkaan ympärysmitta = AB + BC + CD + AD
missä, AB, BC, CD ja ILMOITUS ovat puolisuunnikkaan puolet
Tasakylkisen puolisuunnikkaan ympärysmitta
Jos tasakylkisessä puolisuunnikkaan a ja b ovat yhdensuuntaisten sivujen pituudet eli kantat ja c on kahden yhtä suuren ei-rinnakkaisen sivun pituus, niin kehä saadaan seuraavasti:
Kehä = a + b + 2c
missä,
- a , b ovat Trapeziumin tukikohtia
- c on puolisuunnikkaan tasapuoli
Ero trapetsion ja puolisuunnikkaan välillä
Yleisesti ottaen Trapezium ja Trapezoid ovat samat, mutta ero on niiden alkuperämaassa.
- Trapetsi on brittiläistä alkuperää, se on nelisivuinen monikulmio ja kaksiulotteinen hahmo, jossa on täsmälleen yksi pari toisiaan vastakkaisia yhdensuuntaisia sivuja. Intiassa noudatamme brittiläistä englantia, joten sanaa Trapezium käytetään.
- Trapetsi on amerikkalaista alkuperää, se on myös nelisivuinen monikulmio, jossa on yksi pari yhdensuuntaisia toisiaan vastakkaisia sivuja. Rinnakkaiset sivut ovat pohjat ja toista kahta ei-rinnakkaista sivua kutsutaan puolisuunnikkaan jaloiksi.
Puolisuunnikkaan kulmat
Puolisuunnikas on nelikulmio ja sen kaikkien kulmien summa on 360 astetta. Joten kaikkien puolisuunnikkaan sisäkulmien summa on 360 astetta.
Minkä tahansa säännöllisen puolisuunnikkaan eli puolisuunnikkaan, jossa ei-rinnakkaiset sivut ovat yhtä suuret kuin rinnakkaiset kulmat, jotka muodostuvat yhdensuuntaisen suoran ja ei-rinnakkaisviivan välille, on yhtä suuri. Siten näiden kahden kulman summa on täydentävä.
Otetaan esimerkki tämän käsitteen tukemiseksi tasakylkiselle puolisuunnikkaan ABCD:lle, jos AB on yhdensuuntainen CD:n kanssa ja AD on yhtä kuin CD, niin tiedämme, että ∠A = ∠B ja ∠C = ∠D silloin,
∠A + ∠B + ∠C + ∠D = 360°
Tässä ∠A = ∠B ja ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Vastaavasti (∠B + ∠D) = 180°
Trapetsion diagonaali
Trapetsium on erityinen nelikulmio; näin ollen myös puolisuunnikkaan kaksi diagonaalia. Puolisuunnikkaan diagonaalit eivät ole yhtä pitkiä, toisin kuin joissakin muissa nelikulmioissa, kuten suorakulmioissa tai suunnikkaissa. Puolisuunnikkaan lävistäjät eivät ole yhtä pitkiä ja diagonaalien pituudet riippuvat puolisuunnikkaan kannan pituuksista ja kulmista.
Esimerkki: Tasakylkisen puolisuunnikkaan ABCD kantakulma ∠A on 80° ja etsi sitten toinen kulma ∠C.
Tiedämme, että tasakylkisen puolisuunnikkaan ABCD,
(∠A + ∠C) = 180°
Annettu ∠A = 80°
Nyt 80° + ∠C = 180°
∠C = 180-80
∠C = 100°
Siten vaadittu kulma ∠C on 100°
Puolisuunnikkaan kaavat – Puolisuunnikkaan pinta-ala ja ympärysmitta
Trapetsiumiin liittyvät kaavat on koottu seuraavaan taulukkoon:
| Omaisuus | Kaava |
|---|---|
| Alue | 1/2 × ( a + b ) × h |
| Alue (Isosceles Trapezium) | 1/2 × [√(n2– (a–b)2) (a+b)] |
| Kehä | a + b + c + d |
| Kehä (tasakylkinen puolisuunnikas) | a + b + 2 c |
| Mediaani | (a + b)/2 |
Ihmiset lukevat myös:
voiko luokka laajentaa useita luokkia
- Rombi
- Kolmio
- Mikä on kaava Trapezium-alueen löytämiseksi?
Esimerkkejä trapetsiumista
Esimerkki 1: Etsi puolisuunnikkaan neljäs sivu, jos muut kolme sivua ovat 8 cm, 12 cm ja 16 cm ja ympärysmitta on 40 cm.
Ratkaisu:
Kehä on annettu kaikkien sen sivujen summana. Olkoon pituus o tuntematon 'x' yksikköä.
Kehä = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Tuntemattoman sivun pituus on siis 4 cm
Esimerkki 2: Puolisuunnikkaan yhdensuuntaiset sivut, joiden pituus on 15 cm ja 11 cm, ja ei-rinnakkaiset sivut, joiden pituus on 5 cm. Laske kehä trapetsi.
Ratkaisu:
Se on tasakylkinen puolisuunnikas, koska siinä mainitaan selvästi, että 5 cm:n pituiset sivut ovat yhtä suuret.
Isosceles Trapeziumin mukaan, jos puolisuunnikkaan kaksi ei-rinnakkaista sivua ovat yhtä pitkiä, tunnetaan se isokylkinä puolisuunnikkaana.
Annettu,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Kehä = a + b + 2c
P = 15 + 11 + 2 (5)
P = 15 + 11 + 10
P = 36 cm
Esimerkki 3: Etsi puolisuunnikkaan, jonka sivut ovat 12 cm, 14 cm, 16 cm ja 18 cm, kehä.
Ratkaisu:
P = Kaikkien puolien summa
P = 12 + 14 + 16 + 18
P = 60 cm
Näin ollen puolisuunnikkaan ympärysmitta on 60 cm
Esimerkki 4: Etsi puolisuunnikkaan pinta-ala, jossa yhdensuuntaisten sivujen summa on 60 cm ja korkeus 10 cm.
Ratkaisu:
Annettu,
- Yhdensuuntaisten sivujen summa 60 cm
- korkeus, h = 10 cm
Puolisuunnikkaan pinta-ala, A = 1/2 × yhdensuuntaisten sivujen summa × rinnakkaisten sivujen välinen etäisyys
Annettujen arvojen korvaaminen,
A = 1/2 × 60 × 10
A = 30 × 10
A = 300 cm2
Siksi puolisuunnikkaan pinta-ala = 300 cm2
Harjoittele matematiikan trapeziumin tehtäviä
1. Etsi puolisuunnikkaan pinta-ala, jonka kantat ovat 10 cm ja 15 cm ja korkeus 6 cm.
2. Puolisuunnikkaan pinta-ala on 54 neliömetriä. Jos yksi jalustoista on 12 metriä pitkä ja korkeus 6 metriä, laske toisen jalustan pituus.
3. Laske puolisuunnikkaan kehä, jonka kantat ovat 8 cm ja 14 cm ja sivut 5 cm ja 7 cm.
4. Määritä keskisegmentin pituus puolisuunnikkaan, jossa pohjat ovat 18 cm ja 30 cm.
5. Tasakylkisessä puolisuunnikkaan kulmat yhden kannan kohdalla ovat kukin 45 astetta. Etsi toisen kannan kulmien mitat. Oletetaan, että trapetsi ei ole oikea puolisuunnikkaan.
Yhteenveto – Trapetsium matematiikassa
Puolisuunnikas on nelisivuinen monikulmio tai nelikulmio, jolle on ominaista yksi pari yhdensuuntaisia sivuja, joita kutsutaan kannaksi, kun taas kaksi muuta sivua, jotka tunnetaan jaloina, eivät ole yhdensuuntaisia. Tavallisissa esineissä, kuten pöydissä, yleinen puolisuunnikas on huomattava geometrisista ominaisuuksistaan: sillä on korkeus, joka on kohtisuora etäisyys jalkojen välillä, ja mediaani, joka yhdistää ei-samansuuntaisten sivujen keskipisteet ja on yhdensuuntainen jalkojen kanssa.
Puolisuunnikkaan pinta-ala lasketaan laskemalla pohjan pituuksien keskiarvo ja kertomalla korkeudella, kun taas sen ympärysmitta on sen kaikkien sivujen summa. Eri luokitukset, kuten skaala, tasakylkiset ja oikeat puolisuunnikkaat, joilla kullakin on ainutlaatuiset sivu- ja kulmaominaisuudet, ovat perustavanlaatuisia sekä käytännön sovelluksissa että geometrisessa teoriassa.
Usein kysytyt kysymykset matematiikan Trapeziumista
Mikä on Trapezium Shape?
Puolisuunnikas on nelikulmio, jossa suorapari on aina yhdensuuntainen. Se muistuttaa pöydän muotoa. Sen nimi on peräisin kreikan sanasta trapeze, joka tarkoittaa pöytää.
Kuinka monta trapetsityyppiä?
Trapeziumia on kahta tyyppiä,
- Tavallinen trapezium: Jossa muut suoraparit ovat yhtä suuret.
- Epäsäännöllinen trapetsi: Jossa toinen rivipari ei ole yhtä suuri.
Kuinka monta yhdensuuntaista sivua trapeziumilla on?
Tiedämme, että puolisuunnikas on nelikulmio, jossa on yksi pari yhdensuuntaisia sivuja. Siten trapetsissa on pari yhdensuuntaisia viivoja (sivuja).
Voidaanko puolisuunnikkaan pitää nelikulmio?
A:lla on neljä sivua, neljä kärkeä ja neljä kulmaa. Näin ollen sitä voidaan pitää nelikulmiona, puolisuunnikkaan kaikkien neljän sisäkulman summa on 360 astetta.
Voidaanko neliötä kutsua puolisuunnikkaan?
Puolisuunnikas on nelikulmio, jossa on vain yksi pari yhdensuuntaisia sivuja ja kaksi muuta sivua eivät ole yhdensuuntaisia. Mutta neliön tapauksessa siinä on kaksi paria yhdensuuntaisia sivuja, joten sitä ei voida pitää puolisuunnikkaana.
Ovatko puolisuunnikkaan diagonaalit aina yhtä suuria?
Puolisuunnikkaan diagonaalit eivät välttämättä ole yhtä suuret. Säännöllisen monikulmion tapauksessa diagonaalit ovat yhtä suuret, mutta tämä ei pidä paikkaansa epäsäännöllisen monikulmion tapauksessa.
Mitkä ovat puolisuunnikkaan ominaisuudet?
Trapeziumin 5 ominaisuutta ovat:
- Puolisuunnikkaan emäkset ovat yhdensuuntaiset toistensa kanssa.
- Puolisuunnikkaan on lisäkulmia vierekkäin.
- Vain yksi pari vastakkaisia sivuja on yhdensuuntainen.
- Puolisuunnikkaan sisäkulmien summa on aina 360°.
- Ei-rinnakkaisten sivujen keskipisteen yhdistävä viiva on aina yhdensuuntainen kantaan nähden.
