Kolmion muotoisen pyramidin tilavuus löydetään kaavalla V = 1/3A.H . Kolmion muotoinen pyramidi, joka tunnetaan myös nimellä tetraedri, on eräänlainen pyramidi, jossa on kolmion muotoinen pohja ja kolme kolmion muotoista pintaa, jotka kohtaavat yhdessä pisteessä, jota kutsutaan huipuksi.

Tässä artikkelissa opimme yksityiskohtaisesti pyramidimäärityksestä, kolmiopyramidimäärityksestä, kolmiopyramidikaavasta, esimerkeistä ja muista.

Sisällysluettelo

Android-sovelluksen lukitseminen

• Mikä on pyramidi?
• Kolmiopyramidin määritelmä
• Kolmiopyramidikaava
• Kolmiopyramidin pinta-ala
• Kolmion muotoisen pyramidin tilavuus

Mikä on pyramidi?

A pyramidi pyramidi luokitellaan eri tyyppeihin pohjan muodon perusteella, kuten kolmiopyramidi, neliöpyramidi, viisikulmainen pyramidi, kuusikulmainen pyramidi jne. Huippu on pyramidin sivupintojen tai sivupintojen kohtauskohta . Pystysuora etäisyys pyramidin huipusta sen pohjan keskustaan ​​on pyramidin korkeus tai korkeus. Pyramidin kärjen ja pohjan välinen kohtisuora etäisyys lateraalisen pinnan vinon korkeuden välillä.

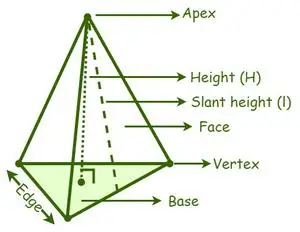
Pyramidi

Kolmiopyramidin määritelmä

Kolmion muotoinen pyramidi on pyramidi, jonka pohjana on kolmio. Se tunnetaan myös tetraedrina, ja siinä on kolme kolmion muotoista pintaa ja yksi kolmiokanta, jossa kolmion kanta voi olla skalaari, tasakylkinen tai tasasivuinen kolmio. Kolmio luokitellaan edelleen kolmeen tyyppiin, eli säännölliseen kolmion muotoiseen pyramidiin, epäsäännölliseen kolmiopyramidiin ja suorakulmaiseen kolmiopyramidiin.

• Tavallinen kolmiopyramidi: Kolmiopyramidia, jonka neljä sivua ovat tasasivuisia kolmioita, kutsutaan säännölliseksi kolmiopyramidiksi. Koska pyramidi koostuu tasasivuisista kolmioista, sen kaikkien sisäkulmien mitta on 60°.

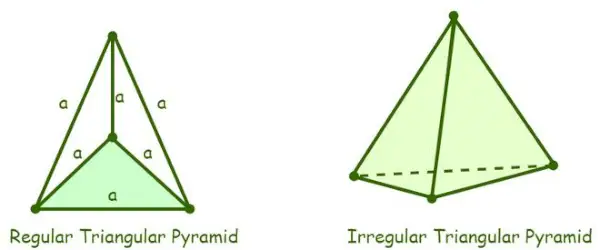
Kolmiopyramidin määritelmä

• Epäsäännöllinen kolmiopyramidi: Epäsäännöllinen kolmiopyramidi on sellainen, jonka kannan reunat eivät ole yhtä suuret, eli epäsäännöllisen kolmion muotoisen pyramidin kanta on joko mittakaavainen kolmio tai tasakylkinen kolmio. Kaikkien kolmiomaisten pyramidien oletetaan olevan säännöllisiä kolmion muotoisia pyramideja, ellei kolmiomaista pyramidia mainita erityisesti epäsäännöllisenä.

• Oikea kolmiopyramidi: Suorakulmainen kolmiopyramidi on pyramidi, jonka kanta on suorakulmainen kolmio ja jonka kärki on kohdistettu kannan keskustan yläpuolelle.

Kolmiopyramidikaava

Kolmiopyramidille on kaksi kaavaa: kolmiopyramidin pinta-ala ja kolmiopyramidin tilavuus.

• Kolmiopyramidin pinta-ala
  • Kolmiopyramidin sivupinta-ala
  • Kolmiopyramidin kokonaispinta-ala
• Kolmion muotoisen pyramidin tilavuus

Kolmiopyramidin pinta-ala

Pyramidin pinta-alalla on kahden tyyppisiä pinta-aloja, nimittäin: sivupinta-ala ja kokonaispinta-ala, jolloin pyramidin pinta-ala on sivupintojen eli sivupintojen pinta-alojen ja pohja-alan summa. pyramidista.

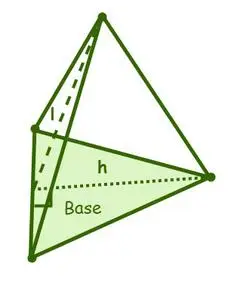
Kolmiopyramidin pinta-ala

Kolmiopyramidin sivupinta-ala

Kolmiopyramidin sivupinta-ala lasketaan kaavalla:

Kolmiopyramidin sivupinta-ala (LSA) = ½ × kehä × vinon korkeus

Kolmiopyramidin kokonaispinta-ala

Pyramidin kokonaispinta-ala (TSA) = pyramidin sivupinta-ala + pohjan pinta-ala

Joten TSA = ½ × kehä × vino korkeus + ½ × pohja × korkeus

Kolmiopyramidin kokonaispinta-ala (TSA) = ½ × P × l + ½ bh

missä,

• P on tukikohdan ympärysmitta
• l on pyramidin vino korkeus
• b on kolmion tukikohta tukikohdassa
• h on pyramidin korkeus

Kolmion muotoisen pyramidin tilavuus

Pyramidin tilavuus on pyramidin kaikkien pintojen välissä oleva kokonaistila. Pyramidin tilavuus esitetään yleensä kirjaimella V, ja sen kaava on yhtä kuin kolmasosa pyramidin perusalan ja korkeuden tulosta.

Pyramidin tilavuuden kaava annetaan seuraavasti:

Kolmiopyramidin tilavuus = 1/3 × pohjapinta-ala × korkeus

V = 1/3 × AH kuutioyksikköä

missä,

• SISÄÄN on Pyramidin tilavuus
• A on pyramidin pohjan alue
• H on pyramidin korkeus tai korkeus

Säännöllisen kolmion muotoisen pyramidin tilavuuden kaava on annettu seuraavasti

poista viimeinen commit git

Säännöllisen kolmiopyramidin tilavuus = a ³ /6√2 kuutioyksikköä

Missä a on Reunojen pituus

Kolmiopyramidiin liittyvä artikkeli:

• Suorakaiteen muotoinen pyramidi
• Neliömäinen pyramidi
• Viisikulmainen pyramidi
• Kuusikulmainen pyramidi
• Pyramidikaavan tilavuus
• Pyramidikaavan pinta-ala

Esimerkkejä kolmiopyramidikaavasta

Esimerkki 1: Määritä kolmiopyramidin tilavuus, jonka pohjapinta-ala ja korkeus ovat 50 cm ² ja 12 cm, vastaavasti.

Ratkaisu:

Annetut tiedot,

• Kolmiopohjan pinta-ala = 100 cm²
• Pyramidin korkeus = 12 cm

Tiedämme sen,

Kolmion muotoisen pyramidin tilavuus (V) = 1/3 × kolmion pohjan pinta-ala × korkeus

K = 1/3 × 50 × 12 = 200 cm³

Näin ollen annetun kolmion muotoisen pyramidin tilavuus on 200 cm³.

java vertailukelpoinen käyttöliittymä

Esimerkki 2: Etsi säännöllisen kolmiopyramidin kokonaispinta-ala, kun kunkin reunan pituus on 8 tuumaa.

Ratkaisu:

Annetut tiedot,

• Säännöllisen kolmiopyramidin kunkin reunan pituus (a) = 8 tuumaa

Tiedämme sen,

Säännöllisen kolmion muotoisen pyramidin kokonaispinta-ala = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 neliötuumaa

Näin ollen säännöllisen kolmion muotoisen pyramidin kokonaispinta-ala on 110,851 neliömetriä.

Esimerkki 3: Määritä säännöllisen kolmion muotoisen pyramidin tilavuus, kun sen reunan pituus on 10 cm.

Ratkaisu:

Annetut tiedot,

• Säännöllisen kolmiopyramidin (a) kunkin reunan pituus = 10 cm

Tiedämme sen,

Säännöllisen kolmion muotoisen pyramidin tilavuus = a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Näin ollen säännöllisen kolmion muotoisen pyramidin tilavuus on 117,85 cu. cm.

Esimerkki 4: Etsi kolmiopyramidin vinon korkeus, jos sen sivupinta-ala on 600 neliötuumaa ja pohjan ympärysmitta on 60 tuumaa.

Ratkaisu:

Annetut tiedot,

• Sivuttaispinta-ala = 600 neliömetriä
• Pohjan ympärysmitta = 60 tuumaa

Tiedämme sen,

Sivuttaispinta-ala = ½ × kehä × vinon korkeus

600 = ½ × 60 × l

l = 600/30 = 20 tuumaa

Näin ollen annetun pyramidin vinon korkeus on 20 tuumaa.

yksinkertainen python-ohjelma

Esimerkki 5: Määritä kolmion muotoisen pyramidin kokonaispinta-ala, jonka pohjapinta-ala on 28 cm2, kolmion ympärysmitta on 18 cm ja pyramidin vinon korkeus on 20 cm.

Ratkaisu:

Annetut tiedot,

• Kolmiopohjan pinta-ala = 28 cm²
• Kallistuskorkeus (l) = 20 cm
• Kehä (P) = 18 cm

Tiedämme sen,

Kolmiopyramidin kokonaispinta-ala (TSA) = ½ × kehä × vinon korkeus + pohjapinta-ala

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 neliöcm

tring to int

Näin ollen annetun pyramidin kokonaispinta-ala on 208 neliöcm.

Harjoittele ongelmia kolmiopyramidikaavalla

Q1. Mikä on pyramidin tilavuus, kun otetaan huomioon kolmiopyramidi, jonka pohjapinta-ala on 15 neliöyksikköä ja korkeus 10 yksikköä?

Q2. Mikä on pyramidin kokonaispinta-ala, kun annetaan säännöllinen kolmiopyramidi, jonka tasasivuisen kolmiomaisen kannan jokainen reuna on 6 yksikköä?

Q3. Mikä on pyramidin tilavuus ja kokonaispinta-ala, kun annetaan säännöllinen kolmiopyramidi, jonka tasasivuisen kolmiomaisen pohjan jokainen reuna on 4 yksikköä ja korkeus 5 yksikköä?

Q4. Jos kolmiopyramidin pohjan sivupituudet ovat 3 yksikköä, 4 yksikköä ja 5 yksikköä ja pyramidin korkeus on 12 yksikköä, mikä on pyramidin tilavuus?

Q5. Kolmiopyramidille, jonka kanta on suorakulmaisen kolmion muotoinen ja jonka jalat ovat 3 yksikköä ja 4 yksikköä ja hypotenuusa 5 yksikköä, mikä on kokonaispinta-ala, jos pyramidin korkeus alustasta kärkeen on 10 yksikköä ?

Usein kysytyt kysymykset kolmiopyramidikaavasta

Mikä on kolmiopyramidin määritelmä?

Kolmion muotoinen pyramidi on geometrinen muoto, jolla on kolmion muotoinen pohja ja kolme kolmion muotoista pintaa, joilla on yhteinen kärki.

Kuinka monta pintaa ja pistettä kolmiopyramidilla on?

Kolmion muotoisella pyramidilla on neljä pintaa ja neljä kärkeä. Yksi kärki on yhteinen kaikille pyramidin kolmelle pinnalle.

Mikä on pyramidin peruskaava?

Pyramidin peruskaavat ovat:

• LSA = ½ × kehä × vinon korkeus
• TSA = ½ × P × l + ½ bh
• V = 1/3 × AH

Mitkä ovat kolmiopyramidityypit?

Kolmion muotoisia pyramideja on kolmenlaisia

• Säännöllinen kolmiopyramidi
• Epäsäännöllinen kolmiopyramidi
• Suorakulmainen kolmiopyramidi

Mikä on kolmioiden kaava?

Kolmion pinta-alan kaava on:

• (pinta-ala) A = 1/2 × b × h