TRIGONOMETRIATAULUKKO

Trigonometriataulukko on vakiotaulukko, joka auttaa meitä löytämään trigonometristen suhteiden arvot standardikulmille, kuten 0°, 30°, 45°, 60° ja 90°. Se koostuu kaikista kuudesta trigonometrisesta suhteesta: sini, kosini, tangentti, kosekantti, sekantti ja kotangentti.

Tutustutaan trigonometriataulukkoon yksityiskohtaisesti.

Sisällysluettelo

Trigonometriataulukko
Trigonometrinen funktiotaulukko
Temppu trigonometristen suhteiden oppimiseen
Kuinka muistaa trigonometrinen taulukko
Trig-taulukon luominen
Trigonometriset kaavat
Trigonometrinen identiteettitaulukko
Esimerkkejä trigonometrisista taulukoista

Trigonometrinen taulukko on kaikkien kuuden trigonometrisen funktion arvojen järjestely niiden yhteisille kulmille taulukkomuodossa.

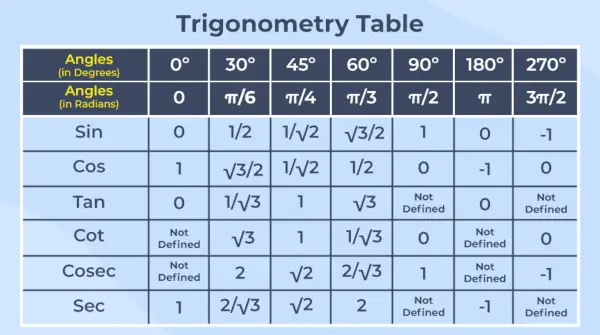
Trigonometriataulukko

Huomautus – Trigonometria on matematiikan haara, joka käsittelee suorakulmaisten kolmioiden kulmien ja sivujen välisiä suhteita.

Trigonometrinen funktiotaulukko

Trigonometrialla on kuusi trigonometrista perusfunktiota, jotka ovat sini, kosini, tangentti, kosekantti, sekantti ja kotangentti. Katsotaanpa nyt trigonometrisiä funktioita.

Jokaiselle suorakulmaiselle kolmiolle, jossa on kohtisuora (P), kanta (B) ja hypotenuusa (H), kuusi trigonometristä funktiota ovat seuraavat:

Trigonometristen funktioiden taulukko
Toiminto	Määritelmä	Edustus	Suhde suorakulmaisen kolmion sivuihin
Hänen	Pystysuoran ja hypotenuusan suhde	ilman i	Vastakkainen puoli / hypotenuusa
Kosini	Pohjan ja hypotenuusan suhde	cos i	Viereinen puoli / hypotenuusa
Tangentti	Kulman sinin ja kosinin suhde	niin i	Vastakkainen puoli / viereinen puoli
Kosekantti	Sin θ käänteisluku	csc i tai cosec i	Hypotenuusa / vastakkainen puoli
Sekantti	Cos θ:n käänteisluku	sek i	Hypotenuusa / viereinen puoli
Kotangentti	Tan θ käänteisluku	pinnasänky i	Viereinen puoli / vastakkainen puoli

Huomautus – Trigonometria on matematiikan haara, joka käsittelee kolmioiden, erityisesti suorakulmaisten kolmioiden, kulmien ja sivujen välisiä suhteita. Se sisältää sini-, kosini-, tangentti- ja muiden trigonometristen funktioiden tutkimisen ja soveltamisen ongelmien ratkaisemiseksi eri aloilla.

Tarkistaa : Trigonometria: kaavat, taulukko, identiteetit ja suhteet

Temppu trigonometristen suhteiden oppimiseen

Tutki alla olevaa taulukkoa oppiaksesi trigonometriset suhteet helposti muistettavalla tavalla.

Joillakin ihmisillä on kiharat mustat hiukset kauneuden tuottamiseksi

sin θ (Jotkut) = kohtisuora (ihmiset) / hypotenuusa (on)

cos θ (kihara) = pohja (musta) / hypotenuusa (hiukset)

tan θ (to) = kohtisuora (tuote) / perusta (kauneus)

Kuinka muistaa trigonometrinen taulukko

Trigonometriataulukko on melko helppo muistaa, jos tiedät kaikki trigonometriakaavat. On myös temppu nimeltä yhden käden temppu muistaaksesi trigonometriataulukon.

Kuinka muistaa trigonometrinen taulukko

Vaihe 1: Yllä olevassa kuvassa, sinitaulukossa, laske vasemman puolen sormet vakiokulmaa varten.

Vaihe 2: Jaa vasemmalla puolella olevien sormien määrä (laske ensimmäisessä vaiheessa) 4:llä

Vaihe 3: Etsi vaiheessa 2 lasketun arvon neliöjuuri.

Tarkistaa: Trigonometriakaavat – Luettelo kaikista trigonometrisista identiteeteistä ja kaavoista

Trig-taulukon luominen

Tutustu seuraaviin vaiheisiin luodaksesi trigonometrisen taulukon standardikulmille.

Vaihe 1: Luo taulukko

Luo taulukko ja luettele kaikki kulmat, kuten 0°, 30°, 45°, 60° ja 90°, ylimmässä rivissä. Syötä kaikki trigonometriset funktiot sin, cos, tan, cosec, sec ja cot ensimmäiseen sarakkeeseen.

Vaihe 2: Arvioi syntifunktion kaikkien kulmien arvo.

Saadaksesi syntifunktion arvot, jaa 0, 1, 2, 3 ja 4 4:llä ja ota kunkin arvon juuren alle, vastaavasti,

Sillä arvo sin 0° = √(0/4) = 0
Samalla lailla,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1

ilman 0°	ilman 30°	ilman 45°	ilman 60°	ilman 90°
0	1/2	1/√2	√3/2	1

Vaihe 3: Arvioi cos-funktion kaikkien kulmien arvo

Cos-funktion arvo on päinvastainen kuin sin-funktion arvo, eli cos 0° = sin 90°, cos 30° = sin 60° ja cos 45° = sin 45°, joten

cos 0°	cos 30°	cos 45°	cos 60°	cos 90°
1	√3/2	1/√2	1/2	0

Vaihe 4: Arvioi kaikkien rusketusfunktion kulmien arvo

Tan-funktion arvo on yhtä suuri kuin sin-funktio jaettuna cos-funktiolla, eli tan x = sin x / cos x. Kaikkien kulmien arvo tan-funktiossa lasketaan seuraavasti:

tan 0° = sin 0° / cos 0° = 0/1 = 0, samoin

siis 0°	siis 30°	siis 45°	siis 60°	siis 90°
0	1/√3	1	√3	Ei määritelty

Vaihe 5: Arvioi cosec-funktion kaikkien kulmien arvo

Cosec-funktion arvo on yhtä suuri kuin sinifunktion käänteisluku. Cosec 0°:n arvo saadaan ottamalla sin 0°:n käänteisluku

cosec 0° = 1 / sin 0° = 1 / 0 = Ei määritelty. Samalla lailla,

cosec 0°	cosec 30°	cosec 45°	cosec 60°	cosec 90°
Ei määritelty	2	√2	23	1

Vaihe 6: Arvioi sek-funktion kaikkien kulmien arvo

Sekuntifunktion arvo on yhtä suuri kuin cos-funktion käänteisluku. Arvo sec 0° saadaan ottamalla cos 0°:n käänteisluku

sek 0° = 1 / cos 0° = 1 / 1 = 1. Vastaavasti

sek 0°	sek 30°	sek 45°	sek 60°	sek 90°
1	23	√2	2	Ei määritelty

Vaihe 7: Arvioi pinnasänkytoiminnon kaikkien kulmien arvo

Pinnasänkyfunktion arvo on yhtä suuri kuin rusketusfunktion käänteisluku. Cot 0°:n arvo saadaan ottamalla tan 0°:n käänteisluku

pinnasänky 0° = 1 /rusketus 0° = 1 / 0 = Ei määritelty. Samalla lailla,

pinnasänky 0°	pinnasänky 30°	pinnasänky 45°	pinnasänky 60°	pinnasänky 90°
Ei määritelty	√3	1	1/√3	0

Tällä tavalla voimme luoda seuraavan trigonometrisen suhdetaulukon:

Asteiden ja radiaanien trigonometrinen taulukko
Kulma (asteina)	Kulma (radiaaneina)	Ilman	Cos	Niin	Cosec	Sec	Pinnasänky
0°	0	0	1	0	Määrittämätön	1	Määrittämätön
30°	p/6	1/2	√3/2	1/√3	2	23	√3
45°	p/4	√2/2	√2/2	1	√2	√2	1
60°	p/3	√3/2	1/2	√3	23	2	1/√3
90°	p/2	1	0	Määrittämätön	1	Määrittämätön	0

Trigonometriset kaavat

Opitaanpa joitain täydentäviin ja täydentäviin kulmiin liittyviä trigonometriakaavoja.

Täydentävät kulmat: Kulmapari, jonka summa on 90°

Lisäkulmat: Kulmapari, jonka summa on 180°

Tarkistaa: Trigonometriset suhteet

Täydentävien kulmien laukaisuiden identiteetit

Täydentävien kulmien identiteetit perustuvat kahden kulman trigonometristen funktioiden väliseen suhteeseen, joiden summa on 90 astetta (tai π/2 radiaania). Nämä tunnetaan nimellä yhteistoiminnalliset identiteetit .

Trigonometrinen funktio	Identiteetti
Hänen	sin(90°− i )=cos i
Kosini	cos(90°− i )=ilman i
Tangentti	tan(90°− i ) = pinnasänky i
Kotangentti	pinnasänky (90°− i )=niin i
Sekantti	sec(90°− i )=csc i
Kosekantti	kosek(90°− i )=sek i

Täydentävien kulmien laukaisuiden identiteetit

Lisäkulmien identiteetit liittyvät kahden kulman trigonometrisiin funktioihin, joiden summa on 180 astetta (tai π radiaania).

Trigonometrinen funktio	Identiteetti
Hänen	sin(180°− i )=ilman i
Kosini	cos(180°− i )=-cos i
Tangentti	tan(180°− i )=-rusketus i
Kotangentti	pinnasänky (180°− i )=− pinnasänky i
Sekantti	sec(180°− i )=−sek i
Kosekantti	kosek(180°− i )=cosec i

Trigonometrinen identiteettitaulukko

Trigonometriset identiteetit ovat identiteetit, joita käytetään paljon trigonometristen ongelmien ratkaisemisessa. On olemassa erilaisia trigonometrisiä identiteettejä, mutta kolme tärkeintä trigonometristä identiteettiä ovat

Trigonometristen identiteettien taulukko
Trigonometrinen identiteetti	Kaava
Pythagoraan identiteetti	ilman²θ + cos²θ = 1
Sekantti-tangentti-identiteetti	sek²θ – niin²θ = 1
Cosecant-Cotangent Identity	cosec²θ – pinnasänky²θ = 1

Tarkista myös:

Trigonometriset suhteet

Käänteiset trigonometriset identiteetit

Korkeudet ja etäisyydet

Esimerkkejä trigonometrisista taulukoista

Ratkaistaan joitain kysymyksiä trigonometrisesta taulukosta.

Esimerkki 1: Jos sin θ = 4/5, niin etsi kaikki trigonometriset arvot.

Ratkaisu:

Tässä meillä on,

sin θ = 4/5

as, sin θ = Perpendicular / Hypotenuse

joten meillä on kohtisuora (P) = 4 ja hypotenuusa (H) = 5

Pythagoras-lauseen mukaan H ² = P ² +B ²

Selvitetään perusarvon (B) arvo

5²= B²+ 4²
25 = B²+ 16
25-16 = B²
B²= 9
B = 3

Nyt meillä on,

Sin θ = kohtisuora/hypotenuusa
= AB/AC = 4/5

Kosini θ = emäs/hypotenuusa
= BC/AC = 3/5

Tangentti θ = kohtisuora/kanta
= AB/BC = 4/3

Kosekantti θ = hypotenuusa/ kohtisuora
= AC/AB = 5/4

Sekantti θ = hypotenuusa/kanta
= AC/BC = 5/3

Kotangentti θ = kanta/ kohtisuora
= BC/AB = 3/4

Esimerkki 2: Etsi cos 45° + 2 sin 60° – tan 60° arvo.

Ratkaisu:

Trigonometriataulukosta,

cos 45° = 1/√2, sin 60° = √3/2 ja tan 60° = √3

Täten,

cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2

Esimerkki 3: Etsi cos 75°:n arvo.

Ratkaisu:

Tiedämme sen,

cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2

cos 75°= (√3 – 1)/2√2.

Johtopäätös – Trigonometriataulukko

Trigonometriataulukko tarjoaa kattavan viittauksen trigonometrisille funktioille sini, kosini, tangentti, kosekantti, sekantti ja kotangentti sekä niiden arvot eri kulmille. minä t toimii arvokkaana ratkaisuna trigonometriset yhtälöt, geometristen suhteiden analysointi ja jaksollisten ilmiöiden käyttäytymisen ymmärtäminen. Onko sisällä matematiikan, fysiikan, tekniikan tai muiden alojen trigonometriataulukko auttaa laskelmissa, ongelmanratkaisussa ja visualisoinnissa, mikä auttaa ymmärtämään paremmin trigonometrisiä käsitteitä ja niiden sovelluksia tosielämän skenaarioissa.