Tämä opetusohjelma on aloittelijaystävällinen opas tietorakenteiden ja algoritmien oppiminen Pythonin avulla. Tässä artikkelissa käsittelemme sisäänrakennettuja tietorakenteita, kuten luetteloita, monikoita, sanakirjoja jne., ja joitain käyttäjän määrittämiä tietorakenteita, kuten esim. linkitetyt luettelot , puita , kaavioita jne. ja läpikulkua sekä haku- ja lajittelualgoritmeja hyvien ja hyvin selitettyjen esimerkkien ja harjoituskysymysten avulla.

Luettelot

Python-listat ovat järjestettyjä tietokokoelmia aivan kuten muiden ohjelmointikielien taulukot. Se sallii erityyppiset elementit luettelossa. Python Listin toteutus on samanlainen kuin Vectors C++:ssa tai ArrayList JAVA:ssa. Kallis toiminto on elementin lisääminen tai poistaminen luettelon alusta, koska kaikkia elementtejä on siirrettävä. Listan lopusta lisääminen ja poistaminen voi myös tulla kalliiksi, jos esivarattu muisti täyttyy.

Esimerkki: Python-luettelon luominen

List = [1, 2, 3, 'GFG', 2.3] print(List)>

[1, 2, 3, 'GFG', 2.3]>

Luettelon elementtejä voi käyttää määritetyllä indeksillä. Listan python-aloitusindeksissä sekvenssi on 0 ja loppuindeksi (jos siinä on N elementtiä) N-1.

Esimerkki: Python List Operations

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3])>

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks>

Tuple

Python-kirjaimet ovat samanlaisia ​​kuin luettelot, mutta Tuples ovat muuttumaton luonnossa eli kerran luotua sitä ei voi muokata. Kuten luettelo, myös Tuple voi sisältää erityyppisiä elementtejä.

Pythonissa monikot luodaan sijoittamalla arvosarja, joka on erotettu 'pilkulla' joko sulkuilla tai ilman datasekvenssin ryhmittelyä.

Huomautus: Jos haluat luoda yhdestä elementistä monikon, sen lopussa on oltava pilkku. Esimerkiksi (8,) luo monikon, jonka elementtinä on 8.

Esimerkki: Python Tuple Operations

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3])>

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4>

Aseta

Python setti on muuttuva datakokoelma, joka ei salli päällekkäisyyttä. Sarjoja käytetään periaatteessa jäsentestaukseen ja päällekkäisten merkintöjen poistamiseen. Tässä käytetty tietorakenne on Hashing, suosittu tekniikka lisätä, poistaa ja kulkea keskimäärin O(1):ssä.

Jos samassa indeksikohdassa on useita arvoja, arvo liitetään kyseiseen indeksipaikkaan linkitettyjen listan muodostamiseksi. Vuonna CPython Sets on toteutettu käyttämällä sanakirjaa, jossa on valemuuttujia, joissa avainolennot jäsenet asettavat suuremmilla optimoinnilla ajan monimutkaisuuteen.

Aseta toteutus:

Sarjat, joissa on useita toimintoja yhdessä hash-taulukossa:

Esimerkki: Python Set Operations

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set)>

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True>

Jäädytetyt sarjat

Jäädytetyt setit Pythonissa ovat muuttumattomia objekteja, jotka tukevat vain menetelmiä ja operaattoreita, jotka tuottavat tuloksen vaikuttamatta jäädytettyyn joukkoon tai sarjoihin, joihin niitä sovelletaan. Vaikka joukon elementtejä voidaan muokata milloin tahansa, jäädytetyn joukon elementit pysyvät samoina luomisen jälkeen.

Esimerkki: Python Frozen -sarja

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h')>

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'})>

merkkijono

Python-merkkijonot on muuttumaton tavutaulukko, joka edustaa Unicode-merkkejä. Pythonilla ei ole merkkitietotyyppiä, yksi merkki on yksinkertaisesti merkkijono, jonka pituus on 1.

Huomautus: Koska merkkijonot ovat muuttumattomia, merkkijonon muokkaaminen johtaa uuden kopion luomiseen.

Esimerkki: Python-merkkijonotoiminnot

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1])>

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s>

Sanakirja

Python-sanakirja on järjestämätön tietojen kokoelma, joka tallentaa tiedot muodossa avain:arvo-pari. Se on kuin hash-taulukot missä tahansa muussa kielessä, jonka aikamonimutkaisuus on O(1). Python-sanakirjan indeksointi tapahtuu avainten avulla. Nämä ovat mitä tahansa tiivistettävää tyyppiä eli objekteja, jotka eivät voi koskaan muuttua, kuten merkkijonot, numerot, monikot jne. Voimme luoda sanakirjan käyttämällä aaltosulkeiden ({}) tai sanakirjan ymmärtämistä.

Esimerkki: Python-sanakirjatoiminnot

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict)>

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25}>

Matriisi

Matriisi on 2D-taulukko, jossa jokainen elementti on täsmälleen samankokoinen. Matriisin luomiseksi käytämme NumPy-paketti .

Esimerkki: Python NumPy Matrix Operations

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m)>

Lähtö

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]]>

Bytearray

Python Bytearray antaa muuttuvan kokonaislukujonon välillä 0 <= x < 256.

Esimerkki: Python Bytearray -toiminnot

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a)>

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')>

Linkitetty lista

A linkitetty lista on lineaarinen tietorakenne, jossa elementtejä ei ole tallennettu vierekkäisiin muistipaikkoihin. Linkitetyn luettelon elementit linkitetään osoittimilla alla olevan kuvan mukaisesti:

Linkitettyä luetteloa edustaa osoitin linkitetyn luettelon ensimmäiseen solmuun. Ensimmäistä solmua kutsutaan pääksi. Jos linkitetty lista on tyhjä, pään arvo on NULL. Jokainen listan solmu koostuu vähintään kahdesta osasta:

• Data
• Osoitin (tai viittaus) seuraavaan solmuun

Esimerkki: Linkitetyn luettelon määrittäminen Pythonissa

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None>

Luodaan yksinkertainen linkitetty luettelo, jossa on 3 solmua.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | nolla | | 3 | nolla |  +----+------+ +----+------+ +----+------+ ''' toinen.seuraava = kolmas ; # Linkitä toinen solmu kolmanteen solmuun ''' Nyt toisen solmun seuraava viittaa kolmanteen. Joten kaikki kolme solmua on linkitetty.  list.head toinen kolmas | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | nolla |  +----+------+ +----+------+ +----+------+ '''>

Linked List Traversal

Edellisessä ohjelmassa olemme luoneet yksinkertaisen linkitetyn luettelon, jossa on kolme solmua. Käydään läpi luotu lista ja tulostetaan kunkin solmun tiedot. Läpikulkua varten kirjoitetaan yleiskäyttöinen funktio printList(), joka tulostaa minkä tahansa listan.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()>

1 2 3>

Lisää artikkeleita linkitetyistä luetteloista

• Linkitetyn luettelon lisäys
• Linkitetyn luettelon poistaminen (tietyn avaimen poistaminen)
• Linkitetyn luettelon poistaminen (avaimen poistaminen annetusta sijainnista)
• Etsi linkitetyn luettelon pituus (iteratiivinen ja rekursiivinen)
• Hae elementtiä linkitetystä luettelosta (iteratiivinen ja rekursiivinen)
• N. solmu linkitetyn luettelon lopusta
• Kääntää linkitetty luettelo

A pino on lineaarinen tietorakenne, joka tallentaa kohteita Last-In/First-Out (LIFO) tai First-In/Last-Out (FILO) tavalla. Pinossa uusi elementti lisätään toiseen päähän ja elementti poistetaan vain siitä päästä. Lisää- ja poistotoimintoja kutsutaan usein push- ja pop-toiminnoiksi.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty>

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []>

Pinona, jonottaa on lineaarinen tietorakenne, joka tallentaa kohteet FIFO (First In First Out) -tavalla. Jonossa viimeksi lisätty kohde poistetaan ensin. Hyvä esimerkki jonosta on mikä tahansa kuluttajien jono resurssille, jossa ensin palvellaan ensin tullutta kuluttajaa.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty>

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []>

Prioriteettijonot ovat abstrakteja tietorakenteita, joissa jokaisella jonon tiedolla/arvolla on tietty prioriteetti. Esimerkiksi lentoyhtiöillä matkatavarat, joiden otsikko on Business tai First Class, saapuvat aikaisemmin kuin muut. Priority Queue on jonon laajennus seuraavilla ominaisuuksilla.

• Korkean prioriteetin elementti poistetaan jonosta ennen matalan prioriteetin elementtiä.
• Jos kahdella elementillä on sama prioriteetti, ne toimitetaan niiden järjestyksen mukaan jonossa.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] palauttaa kohteen paitsi IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) mutta ei myQueue.isEmpty(): print(myQueue.delete())>

12 1 14 7 14 12 7 1>

Pino

heapq-moduuli Pythonissa tarjoaa keon tietorakenteen, jota käytetään pääasiassa edustamaan prioriteettijonoa. Tämän tietorakenteen ominaisuus on, että se antaa aina pienimmän elementin (min kasan) aina kun elementti pompataan. Aina kun elementtejä työnnetään tai poksetaan, kasarakenne säilyy. Hep[0]-elementti palauttaa myös pienimmän elementin joka kerta. Se tukee pienimmän elementin poistamista ja lisäämistä O(log n)-ajoissa.

Yleensä kasoja voi olla kahta tyyppiä:

• Max-keko: Max-Heapissa juurisolmussa olevan avaimen on oltava suurin kaikissa sen lapsissa olevista avaimista. Saman ominaisuuden on oltava rekursiivisesti totta kaikille kyseisen binaaripuun alipuille.
• Vähimmäiskeko: Min-Keapissa juurisolmussa olevan avaimen on oltava pienin kaikkien sen alaryhmien avainten joukossa. Saman ominaisuuden on oltava rekursiivisesti totta kaikille kyseisen binaaripuun alipuille.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li))>

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1>

Lisää artikkeleita Heapista

• Binäärikasa
• K':n suurin elementti taulukossa
• K'th pienin/suurin elementti lajittelemattomassa taulukossa
• Lajittele lähes lajiteltu matriisi
• K. suurimman summan vierekkäinen alialue
• Kahden taulukon numeroista muodostetun luvun vähimmäissumma

Puu on hierarkkinen tietorakenne, joka näyttää alla olevasta kuvasta -

 tree  ----  j <-- root  /   f k  /   a h z <-- leaves>

Puun ylintä solmua kutsutaan juureksi, kun taas alimpia solmuja tai solmuja, joissa ei ole lapsia, kutsutaan lehtisolmuiksi. Solmuja, jotka ovat suoraan solmun alla, kutsutaan sen lapsiksi ja solmuja, jotka ovat suoraan jonkin solmun yläpuolella, kutsutaan sen yläpääksi.

A binäärinen puu on puu, jonka elementeillä voi olla melkein kaksi lasta. Koska jokaisella binääripuun elementillä voi olla vain 2 alaosaa, annamme yleensä nimet vasemmalle ja oikealle lapselle. Binaaripuusolmu sisältää seuraavat osat.

• Data
• Osoitin vasemmalle lapselle
• Osoita oikeaa lasta

Esimerkki: Solmuluokan määrittäminen

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key>

Luodaan nyt puu, jossa on 4 solmua Pythonissa. Oletetaan, että puurakenne näyttää alla olevalta -

 tree  ----  1 <-- root  /   2 3   /  4>

Esimerkki: Tietojen lisääminen puuhun

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None'''>

Puun läpikulku

Puut voidaan ajella eri tavoin. Seuraavassa on yleisesti käytettyjä tapoja puiden ylittämiseen. Tarkastellaanpa alla olevaa puuta -

 tree  ----  1 <-- root  /   2 3   /  4 5>

Syvyys ensimmäiset matkat:

• Järjestys (vasen, juuri, oikea): 4 2 5 1 3
• Ennakkotilaus (juuri, vasen, oikea): 1 2 4 5 3
• Postorder (vasen, oikea, juuri): 4 5 2 3 1

Algoritmin järjestys(puu)

• Kävele vasemman alipuun läpi, eli kutsu Inorder(vasen-alipuu)
• Vieraile juurella.
• Kulje oikeanpuoleisen alipuun läpi, eli kutsu Inorder(oikea-alipuu)

Algoritmin ennakkotilaus (puu)

• Vieraile juurella.
• Kävele vasemman alipuun läpi, eli kutsu Preorder(left-subtree)
• Kulje oikeanpuoleisen alipuun läpi, eli kutsu Preorder(oikea-alipuu)

Algoritmi Postimääräys (puu)

• Kävele vasemman alipuun läpi, eli kutsu Postorder(vasen-alipuu)
• Kulje oikeanpuoleisen alipuun läpi, eli kutsu Postorder(oikea-alipuu)
• Vieraile juurella.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root)>

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1>

Aika monimutkaisuus – O(n)

Leveys-First tai Level Order Traversal

Tasotilauksen läpikulku puu on leveys-ensimmäinen läpikulku puulle. Yllä olevan puun tasojärjestyksen läpikulku on 1 2 3 4 5.

valinta lajittelu

Jokaisen solmun kohdalla käydään ensin solmussa ja sitten sen lapsisolmut asetetaan FIFO-jonoon. Alla on algoritmi samalle -

• Luo tyhjä jono q
• temp_node = juuri /*aloita juuresta*/
• Silmukka kun temp_node ei ole NULL
  • tulosta temp_node-> data.
  • Jonota temp_node:n lapset (ensin vasen ja sitten oikea lapsi) kohtaan q
  • Pura solmu q:sta

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Tulosta jonon etuosa ja # poista se jonosta print (queue[0].data) node = queue.pop(0) # Lisää jonoon vasen lapsi, jos node.left ei ole Ei mitään: queue.append(node.left ) # Lisää jonoon oikea lapsi, jos solmu.oikea ei ole Ei mitään: queue.append(node.right) # Ohjainohjelma testattava yllä oleva funktio root = Solmu(1) root.left = Solmu(2) root.right = Node(3) root.left.left = Solmu(4) root.left.right = Solmu(5) print ('Tasojärjestys Binääripuun läpikäynti on -') printLevelOrder(root)>

Level Order Traversal of binary tree is - 1 2 3 4 5>

Aika monimutkaisuus: O(n)

Lisää artikkeleita Binaaripuusta

• Lisäys binaaripuuhun
• Poistaminen binääripuussa
• Inorder Tree Traversal ilman rekursiota
• Inorder Tree Traversal ilman rekursiota ja ilman pinoa!
• Tulosta postorder-läpikulku annetuista tilaus- ja ennakkotilauskierroksista
• Etsi BST:n postorder traversal preorder traversalista

Binäärihakupuu on solmupohjainen binääripuutietorakenne, jolla on seuraavat ominaisuudet:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)>

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)>

20 30 40 50 60 70 80>

A kaavio on epälineaarinen tietorakenne, joka koostuu solmuista ja reunoista. Solmuja kutsutaan joskus myös kärkipisteiksi ja reunat ovat viivoja tai kaaria, jotka yhdistävät mitä tahansa kahta graafin solmua. Muodollisemmin Graafi voidaan määritellä kuvaajaksi, joka koostuu äärellisestä joukosta pisteitä (tai solmuja) ja joukosta reunoja, jotka yhdistävät solmuparin.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0<=vtx<=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix())>

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Ohjainohjelma yllä olevaan kuvaajaluokkaan if __name__ == '__main__' : V = 5 kaavio = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph()>

Adjacency list of vertex 0 head ->4 -> 1 vierekkäisyyslista kärjestä 1 pää -> 4 -> 3 -> 2 -> 0 vierekkäisyyslista kärjestä 2 pää -> 3 -> 1 vierekkäinen luettelo kärjestä 3 pää -> 4 -> 2 -> 1 vierekkäisyys lista kärjestä 4 head -> 3 -> 1 -> 0>> 
Kaavion läpikulku
Breadth-First Search tai BFS 
    Breadth-First Traversal  kaavio on samanlainen kuin puun leveys-ensimmäinen läpikulku. Ainoa saalis tässä on, toisin kuin puut, graafit voivat sisältää syklejä, joten voimme päästä samaan solmuun uudelleen. Jotta vältetään solmun käsittely useammin kuin kerran, käytämme loogista vierailtua taulukkoa. Yksinkertaisuuden vuoksi oletetaan, että kaikki kärjet ovat saavutettavissa aloituspisteestä.
 
Esimerkiksi seuraavassa graafissa aloitamme kulkemisen kärjestä 2. Kun saavumme kärkeen 0, etsimme sen kaikki vierekkäiset kärjet. 2 on myös 0:n viereinen kärkipiste. Jos emme merkitse vierailtuja pisteitä, 2 käsitellään uudelleen ja siitä tulee ei-päättyvä prosessi. Seuraavan kaavion Leveys-First Traversal on 2, 0, 3, 1.
 
  
Python 3 
# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2)>
   
  Lähtö  Aika monimutkaisuus: O(V+E) missä V on graafin kärkien lukumäärä ja E on graafin reunojen lukumäärä.
 
Syvyys ensimmäinen haku tai DFS
  Syvyys ensimmäinen läpikulku  kaavio on samanlainen kuin puun syvyys ensimmäinen läpikulku. Ainoa saalis tässä on, toisin kuin puut, kaaviot voivat sisältää jaksoja, solmussa voidaan käydä kahdesti. Voit välttää solmun käsittelyn useammin kuin kerran käyttämällä loogista vierailtua taulukkoa.
 
    Algoritmi:    
 
Luo rekursiivinen funktio, joka ottaa solmun indeksin ja vieraillun taulukon.
Merkitse nykyinen solmu vierailluksi ja tulosta solmu.
Käy läpi kaikki viereiset ja merkitsemättömät solmut ja kutsu rekursiivista funktiota viereisen solmun indeksillä.
Python 3 
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2)>
   
  Lähtö  
Following is DFS from (starting from vertex 2) 2 0 1 3>
 
Lisää artikkeleita kaaviosta
 Graafiset esitykset joukkoa ja tiivistettä käyttäen 
 Etsi emopiste kaaviosta 
 Iteratiivinen syvyys ensimmäinen haku 
 Laske solmujen määrä tietyllä tasolla puussa käyttämällä BFS:ää 
 Laske kaikki mahdolliset polut kahden kärjen välillä 
 Prosessia, jossa funktio kutsuu itseään suoraan tai epäsuorasti, kutsutaan rekursioksi ja vastaavaa funktiota kutsutaan a  rekursiivinen funktio . Rekursiivisten algoritmien avulla tietyt ongelmat voidaan ratkaista melko helposti. Esimerkkejä tällaisista ongelmista ovat Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph jne. 
  
Mikä on perusehto rekursiossa?
Rekursiivisessa ohjelmassa tarjotaan ratkaisu perustapaukseen ja suuremman ongelman ratkaisu ilmaistaan ​​pienempinä ongelmina.
 
def fact(n):  # base case  if (n <= 1)   return 1  else   return n*fact(n-1)>
Yllä olevassa esimerkissä perustapaus arvolle n <= 1 on määritelty ja suurempi luvun arvo voidaan ratkaista muuttamalla pienemmäksi, kunnes perustapaus saavutetaan.
 
Miten muistia varataan eri funktiokutsuille rekursiossa?
Kun mitä tahansa funktiota kutsutaan main(:sta), sille varataan muisti pinossa. Rekursiivinen funktio kutsuu itseään, kutsutun funktion muisti varataan kutsuvalle funktiolle varatun muistin päälle ja jokaiselle funktiokutsulle luodaan eri kopio paikallisista muuttujista. Kun perustapaus saavutetaan, funktio palauttaa arvonsa funktiolle, joka kutsuu sitä ja muisti puretaan ja prosessi jatkuu.
 
Otetaan esimerkki siitä, kuinka rekursio toimii ottamalla yksinkertainen funktio.
Python 3 
# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)>
   
  Lähtö  
3 2 1 1 2 3>
 
Muistipino on esitetty alla olevassa kaaviossa.
 
 
 
Lisää artikkeleita Recursionista 
 
 Rekursio  
    Rekursio Pythonissa  
 Rekursion harjoituskysymyksiä | Sarja 1 
 Rekursion harjoituskysymyksiä | Sarja 2 
 Rekursion harjoituskysymyksiä | Sarja 3 
 Rekursion harjoituskysymyksiä | Sarja 4 
 Rekursion harjoituskysymyksiä | Sarja 5 
 Rekursion harjoituskysymyksiä | Sarja 6 
 Rekursion harjoituskysymyksiä | Sarja 7 
     >>> Lisää     
 
    Dynaaminen ohjelmointi    
  Dynaaminen ohjelmointi  on pääasiassa optimointia pelkällä rekursiolla. Aina kun näemme rekursiivisen ratkaisun, jossa on toistuvia kutsuja samoihin tuloihin, voimme optimoida sen dynaamisen ohjelmoinnin avulla. Ajatuksena on yksinkertaisesti tallentaa osaongelmien tulokset, jotta meidän ei tarvitse laskea niitä uudelleen tarvittaessa myöhemmin. Tämä yksinkertainen optimointi vähentää aikamonimutkaisuutta eksponentiaalisesta polynomiin. Jos esimerkiksi kirjoitamme yksinkertaisen rekursiivisen ratkaisun Fibonacci-luvuille, saamme eksponentiaalisen aikamonimutkaisuuden ja jos optimoimme sen tallentamalla aliongelmien ratkaisuja, aikamonimutkaisuus pienenee lineaariseksi.
 
 
 
Taulukko vs muistiinpano
Arvot voidaan tallentaa kahdella eri tavalla, jotta aliongelman arvoja voidaan käyttää uudelleen. Tässä käsitellään kahta mallia dynaamisen ohjelmoinnin (DP) ongelman ratkaisemiseksi:
 
    Taulukko:    Alhaalta ylös
    Muistiinpano:    Ylhäältä alas
Taulukko
Kuten nimi itsessään viittaa, aloita alhaalta ja kerää vastauksia ylös. Keskustellaan valtionvaihdoksesta.
 
Kuvataan DP-ongelmamme tilaksi dp[x], jossa dp[0] on perustila ja dp[n] kohdetilana. Joten meidän on löydettävä kohdetilan arvo eli dp[n].
 
Jos aloitamme siirtymisemme perustilastamme eli dp[0] ja seuraamme tilasiirtymäsuhdettamme saavuttaaksemme kohdetilan dp[n], kutsumme sitä alhaalta ylös -lähestymistapaksi, koska on aivan selvää, että aloitimme siirtymisemme alimman perustilan ja saavutti ylimmän halutun tilan.
 
Miksi kutsumme sitä taulukkomenetelmäksi?
 
Tietääksesi tämän, kirjoitetaan ensin koodi luvun kertoimen laskemiseksi alhaalta ylös -lähestymistapaa käyttäen. Jälleen kerran yleisenä menettelynä DP:n ratkaisemiseksi määrittelemme ensin tilan. Tässä tapauksessa määritetään tilaksi dp[x], jossa dp[x] on x:n kertoimen löytäminen.
 
Nyt on aivan ilmeistä, että dp[x+1] = dp[x] * (x+1)
 
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i>
Memoisointi
Kuvataanpa sitä vielä kerran tilasiirtymän kannalta. Jos jollekin tilalle pitää löytää arvo, sano dp[n] ja sen sijaan, että lähdettäisiin perustilasta eli dp[0], kysytään vastausta tiloista, jotka voivat saavuttaa kohdetilan dp[n] tilasiirtymän jälkeen Se on DP:n ylhäältä alas -muoti.
 
Tässä aloitamme matkamme ylimmästä määrätilasta ja laskemme sen vastauksen ottamalla huomioon niiden tilojen arvot, jotka voivat saavuttaa kohdetilan, kunnes saavutamme alimman perustilan.
 
Jälleen kerran kirjoitetaan tekijäongelman koodi ylhäältä alaspäin
 
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1))>
 
 
Lisää artikkeleita dynaamisesta ohjelmoinnista
 Optimaalinen alustan ominaisuus 
 Päällekkäiset aliongelmat -ominaisuus 
  Fibonaccin numerot  
 Osajoukko, jonka summa on jaollinen m:llä 
 Suurin summa, joka lisää jaksoa 
 Pisin yhteinen alimerkkijono 
      >>> Lisää      
 
Hakualgoritmit
Lineaarinen haku
Aloita arr[]:n vasemmanpuoleisesta elementistä ja vertaa x:ää yksitellen jokaiseen arr[]-elementtiin
Jos x vastaa elementtiä, palauta indeksi.
Jos x ei täsmää minkään elementin kanssa, palauta -1.
 
  
Python 3 
# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result)>
   
  Lähtö  
Element is present at index 3>
 
Yllä olevan algoritmin aikamonimutkaisuus on O(n).
 
Lisätietoja on kohdassa Lineaarinen haku .
 
Binäärihaku
Hae lajiteltua taulukkoa jakamalla hakuväli toistuvasti puoliksi. Aloita intervallista, joka kattaa koko taulukon. Jos hakunäppäimen arvo on pienempi kuin välin keskellä oleva kohde, kavenna väli alempaan puoliskoon. Muussa tapauksessa kavenna se yläosaan. Tarkista toistuvasti, kunnes arvo löytyy tai väli on tyhjä.
 
  
Python 3 
# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Jos elementti on itse keskellä jos arr[mid] == x: return mid # Jos elementti on pienempi kuin mid, se # voi olla vain läsnä vasemmassa alijärjestelmässä elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # Muutoin elementti voi olla läsnä vain # oikeassa alijärjestelmässä else: return binarySearch(arr, mid + 1, r, x ) else: # Elementti ei ole taulukossa return -1 # Ohjainkoodi arr = [ 2, 3, 4, 10, 40 ] x = 10 # Funktiokutsun tulos = binarySearch(arr, 0, len(arr)-1 , x) if result != -1: print ('Elementti on indeksissä % d' % tulos) else: print ('Elementti ei ole taulukossa')>
   
  Lähtö  
Element is present at index 3>
 
Yllä olevan algoritmin aikamonimutkaisuus on O(log(n)).
 
Lisätietoja on kohdassa  Binäärihaku  .
 
Lajittelualgoritmit
Valinta Lajittele
The  valinta lajittelu  Algoritmi lajittelee taulukon etsimällä toistuvasti vähimmäiselementin (nousevassa järjestyksessä) lajittelemattomasta osasta ja sijoittamalla sen alkuun. Jokaisessa valintalajittelun iteraatiossa vähimmäiselementti (nousevassa järjestyksessä) lajittelemattomasta alitaulukosta poimitaan ja siirretään lajiteltuun alitaulukkoon.
 
Valinnan lajittelun vuokaavio:
 
  
Python 3 
# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Vaihda löydetty minimielementti #:llä ensimmäisellä elementillä A[i], A[min_idx] = A[min_idx], A[i] # Testattava ohjainkoodi yllä olevan tulosteen ('Sorted array) ') i:lle alueella(len(A)): print('%d' %A[i]),>
   
  Lähtö  
Sorted array 11 12 22 25 64>
 
    Aika monimutkaisuus:    Päällä2), koska siinä on kaksi sisäkkäistä silmukkaa.
 
    Aputila:    O(1)
 
Kuplalajittelu
  Kuplalajittelu  on yksinkertaisin lajittelualgoritmi, joka toimii vaihtamalla toistuvasti vierekkäisiä elementtejä, jos ne ovat väärässä järjestyksessä.
 
    Kuva :    
 
  
Python 3 
# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Testattava kuljettajakoodi yllä arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Lajiteltu matriisi on:') for i in range(len(arr)): print ('%d' %arr[i]),>
   
  Lähtö  
Sorted array is: 11 12 22 25 34 64 90>
 
    Aika monimutkaisuus:    Päällä2)
 
Lisäys Lajittele
Lajitellaksesi n-koon taulukon nousevaan järjestykseen käyttämällä  lisäyslajittelu  :
 
Toisto arr[1]:stä arr[n]:iin taulukon yli.
Vertaa nykyistä elementtiä (avainta) edeltäjäänsä.
Jos avainelementti on pienempi kuin edeltäjänsä, vertaa sitä edellisiin elementteihin. Siirrä suurempia elementtejä yksi paikka ylöspäin, jotta vaihdetulle elementille tulee tilaa.
    Kuva:    
 
  
Python 3 
# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 ja avain< arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i])>
   
  Lähtö  
 5 6 11 12 13>
 
    Aika monimutkaisuus:    Päällä2))
 
Yhdistä lajittelu
Kuten QuickSort,  Yhdistä lajittelu  on hajota ja hallitse -algoritmi. Se jakaa syöttötaulukon kahteen puolikkaaseen, kutsuu itseään kahdeksi puolikkaaksi ja yhdistää sitten kaksi lajiteltua puoliskoa. Merge()-funktiota käytetään kahden puolikkaan yhdistämiseen. Yhdistäminen (arr, l, m, r) on avainprosessi, joka olettaa, että arr[l..m] ja arr[m+1..r] lajitellaan ja yhdistää kaksi lajiteltua alitaulukkoa yhdeksi.
 
MergeSort(arr[], l, r) If r>l 1. Etsi keskipiste jakaaksesi taulukon kahteen puolikkaaseen: keskim = l+ (r-l)/2 2. Soita mergeSort ensimmäiselle puolikkaalle: Soita mergeSort(arr, l, m) 3. Soita mergeLajittele toinen puolisko: Soita mergeSort(arr, m+1, r) 4. Yhdistä vaiheissa 2 ja 3 lajitellut puolikkaat: Kutsu merge(arr, l, m, r)>
 
  
Python 3 
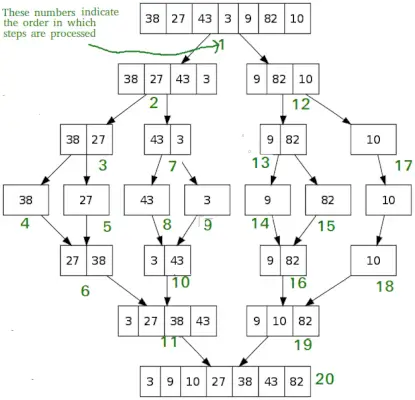
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Taulukon keskikohdan löytäminen mid = len(arr)//2 # Matriisielementtien jakaminen L = arr[:mid] # kahteen puolikkaaseen R = arr[mid:] # Ensimmäisen puolikkaan lajittelu mergeSort(L) # Toisen puoliskon lajittelu mergeSort(R) i = j = k = 0 # Kopioi tiedot väliaikaisiin taulukoihin L[] ja R[] samalla kun i< len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr)>
   
  Lähtö  
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13>
 
    Aika monimutkaisuus:    O(n(logn))
 
QuickSort
Kuten yhdistämislajittelu,  QuickSort  on hajota ja hallitse -algoritmi. Se valitsee elementin pivotiksi ja jakaa annetun taulukon valitun pivotin ympärille. QuickSortista on monia eri versioita, jotka valitsevat nivelen eri tavoilla.
 
Valitse aina ensimmäinen elementti pivoiksi.
 
Valitse aina viimeinen elementti pivoiksi (toteutettu alla)
Valitse satunnainen elementti pivotiksi.
Valitse kääntöpisteeksi mediaani.
QuickSortin avainprosessi on partition(). Osioiden kohde on, kun taulukon ja taulukon elementin x pivotiksi annetaan, x asetetaan oikeaan paikkaansa lajiteltuun taulukkoon ja kaikki pienemmät elementit (pienemmät kuin x) x:n eteen ja kaikki suuremmat elementit (suuremmat kuin x) sen jälkeen. x. Kaikki tämä tulisi tehdä lineaarisessa ajassa.
 
/* low -->Aloitusindeksi, korkea --> Loppuindeksi */ quickSort(arr[], matala, korkea) { if (low { /* pi on osiointiindeksi, arr[pi] on nyt oikeassa paikassa */ pi = osio(arr, matala, korkea);
 
 
    Osioalgoritmi    
 
Osiointia voi tehdä monella eri tavalla  pseudokoodi  käyttää CLRS-kirjassa annettua menetelmää. Logiikka on yksinkertainen, aloitamme vasemmanpuoleisesta elementistä ja seuraamme pienempien (tai yhtä suurien) elementtien indeksiä kuten i. Ajettaessa, jos löydämme pienemmän elementin, vaihdamme nykyisen elementin arr[i]:lla. Muussa tapauksessa ohitamme nykyisen elementin.
  
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start < end: # Increment the start pointer till it finds an # element greater than pivot while start < len(array) and array[start] <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivot: end -= 1 # Jos alku ja loppu eivät ole risteäneet, # vaihda numerot alussa ja lopussa if(alku< end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}')>
   
  Lähtö  
Sorted array: [1, 5, 7, 8, 9, 10]>
 
    Aika monimutkaisuus:    O(n(logn))
 
ShellSort
 ShellSort on pääasiassa lisäyslajittelun muunnelma. Lisäyslajittelussa siirrämme elementtejä vain yhden kohdan eteenpäin. Kun elementtiä on siirrettävä kauas eteenpäin, siihen liittyy monia liikkeitä. ShellSortin idea on mahdollistaa kaukana olevien kohteiden vaihto. ShellSortissa taulukosta tehdään h-lajiteltu suuri h:n arvo. Jatkamme h:n arvon pienentämistä, kunnes siitä tulee 1. Taulukon sanotaan olevan h-lajiteltu, jos jokaisen h:n kaikki alilistatthelementti on lajiteltu.
Python 3 
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = aukko # tarkista taulukko vasemmalta oikealle # viimeiseen mahdolliseen indeksiin j samalla kun j< len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # nyt, katsomme taaksepäin i:nnestä indeksistä vasemmalle # vaihdamme arvot, jotka eivät ole oikeassa järjestyksessä. k = i, kun taas k - väli> -1: jos arr[k - väli]> arr[k]: arr[k-rako],arr[k] = arr[k],arr[k-väli] k -= 1 aukko //= 2 # ajuri koodin tarkistamiseksi arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('lajiteltu array', arr2)>>  
  Lähtö      Aika monimutkaisuus:    Päällä2).