logo

TechCodeview

Alueen kaavat

Alueen kaavat eri kohteille ovat kaavat, joita käytetään eri objektien alueen löytämiseen. Pinta-ala on minkä tahansa hahmon rajan viemä tila. Erilaisten geometristen muotojen pintakaavat ovat riippuvaisia ​​useista parametreista, kuten eri geometristen muotojen mitoista, korkeudesta ja säteestä. Geometrisiä muotoja on kahta tyyppiä, jotka ovat:

  • Kaksiulotteiset muodot (2-D-muodot)
  • Kolmiulotteiset muodot (3D-muodot)

Tässä artikkelissa opimme pintakaavoja erilaisille 2-D- ja 3-D-muodoille, kuten suorakulmion pinta-ala, neliön pinta-ala, ympyrän pinta-ala, kuution pinta-ala jne. ja muita yksityiskohtaisesti.



Sisällysluettelo

Mikä on Area?

Kuvan rajan viemää tilaa kutsutaan kuvion alueeksi. Se mitataan neliöyksikkönä. SI-yksikkö alueen mittaamiseksi on m2. Pinta-alaa käytetään erilaisissa matemaattisissa käsitteissä, ja sitä käytetään myös tosielämän skenaarioissa, kuten huoneen pinta-alan, pinta-alan taulukon jne. ja muiden löytämiseen.

Mitä ovat aluekaavat?

Alueen kaavat ovat olennaisia ​​työkaluja, joita käytetään matematiikassa erilaisten kaksiulotteisten muotojen ympäröimän tilan määrän laskemiseen. Näitä kaavoja voidaan käyttää geometrisen alueen löytämiseen hahmot, kuten neliöt, suorakulmiot, ympyrät, kolmiot, puolisuunnikkaat ja ellipsit. Näitä kaavoja käyttämällä voimme laskea tarkasti eri muotojen pinta-alat, jolloin voimme ratkaista todellisia ongelmia ja tehdä tärkeitä laskelmia.



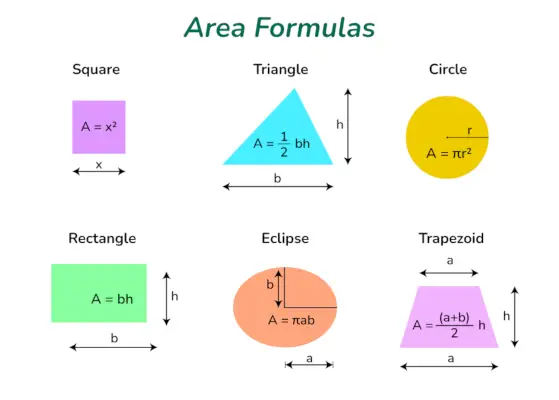
Alue-kaavat

Alueen kaavat

Mitä ovat 2D-muodot?

Muotoja, joilla on vain kaksi ulottuvuutta, kutsutaan nimellä 2-D muodot . Ne on piirretty 2-D-avaruudessa ja ovat riippuvaisia 2 parametria, yleensä pituus (l) ja leveys (b). Erilaiset 2D-muodot ovat Suorakulmio, neliö, kolmio, ympyrät ja muut.

2D-muotojen kaavan alue

2D-muotojen pinta-alakaavat ovat kaavoja, joita käytetään erilaisten 2D-muotojen pinta-alan miellyttämiseen, kuten kolmion pinta-ala, neliön pinta-ala, suorakulmion pinta-ala, rombin pinta-ala jne. Näitä aluekaavoja käytetään paljon matematiikassa ratkaista erilaisia ​​geometrisia ongelmia. Erilaisia ​​aluekaavoja eri muodoille ovat,



Suorakulmion aluekaava

Suorakulmio on 2-ulotteinen kuvio joka on nelikulmio, eli sillä on neljä sivua sen vastakkaiset sivut ovat yhdensuuntaiset ja yhtä suuret. Kaikki suorakulmion kulmat ovat yhtä suuret ja niiden mitta on 90 astetta. Suorakulmion lävistäjät ovat yhtä suuret ja ne ovat kohtisuorassa toisiinsa nähden.

Suorakulmion pinta-alan laskentakaava on pituudella ja l ja leveys b On,

  • Suorakulmion pinta-ala (A) = l×b neliöyksikköä

Neliön aluekaava

Neliö on kaksiulotteinen kuvio, joka on nelikulmio, eli sillä on neljä sivua sen vastakkaiset sivut ovat yhdensuuntaiset ja neliön kaikki neljä sivua ovat yhtä suuret. Kaikki neliön kulmat ovat yhtä suuret ja niiden mitta on 90 astetta. Neliön lävistäjät ovat yhtä suuret ja ne ovat kohtisuorassa toisiinsa nähden.

Kaava neliön, jossa on sivu, pinta-alan laskentakaava a On,

  • Neliön pinta-ala (A) = a 2 neliöyksikköä

Kolmion pintakaava

Kolmio on yksinkertaisin monikulmio, joka tehdään yhdistämällä kolme suoraa. Kuten nimestä voi päätellä, se on monikulmio, jossa on kolme kulmaa. Kolmion kaikkien sivujen pituuksien summa on kolmion kehä ja kolmion kehän sisällä oleva tila on kolmion pinta-ala.

kuinka lähettää merkkijono int: hen javassa

Kaava kantavan kolmion pinta-alan laskemiseksi b on ja korkeus h On,

  • Kolmion pinta-ala (A) = 1/2 × bh neliöyksikköä

Ympyrän aluekaava

Ympyrä on geometrinen kuvio, jossa ei ole suoraa viivaa. Se on pisteen paikka, joka on aina vakioetäisyydellä kiinteästä pisteestä. Kiinteä piste kutsutaan ympyrän keskipisteeksi ja kiinteä etäisyys on ympyrän säde.

Laskekaava ympyrän alue jossa r on ympyrän säde,

  • Ympyrän pinta-ala (A) = πr 2 neliöyksikköä

Suuntaviivan pintakaava

Parallelogrammi on kaksiulotteinen kuvio jossa vastakkaiset sivut ovat yhdensuuntaiset ja yhtä suuret. Kaava suunnikkaan pinta-alan laskemiseksi kantaan b ja korkeus h ovat,

  • Parallelogrammin pinta-ala (A) = bh neliöyksikköä

Rombin aluekaava

Rombi on nelikulmio, jonka kaikki neljä sivua ovat yhtä suuret ja yhdensuuntaiset, mutta kaikki kulmat eivät ole yhtä suuria. Kaava rombin pinta-alan laskemiseksi diagonaalilla d 1 ja d 2 ovat,

  • Rombin pinta-ala (A) = 1/2 × d 1 × d 2 neliöyksikköä

Trapetsin pintakaava

Trapezoid on toinen nimi trapetsi . Se on nelikulmio, jonka vastakkaiset sivut ovat yhdensuuntaiset. Kaava puolisuunnikkaan pinta-alan laskemiseksi yhdensuuntaisilla sivuilla a ja b ja korkeus h On,

  • Puolisuunnikkaan pinta-ala (A) = 1/2(a +b)h neliöyksikköä

Ellipsin aluekaava

Ellipsi on kaksiulotteinen muoto ja se tulee kartiomaisten osien alle. Kaava ellipsin pinta-alan laskemiseksi, jonka akseli on as a ja b ovat,

  • Ellipsin pinta-ala (A) = πab neliöyksikköä

Puoliympyrän pintakaava

Puoliympyrä on 2D-hahmo, joka on puolet ympyrästä. Kaava, jolla lasketaan puoliympyrän, jonka säde on r, pinta-ala on,

  • Puoliympyrän pinta-ala (A) = 1/4(πr 2 ) neliöyksikköä

Aluekaavojen taulukko

Eri 2D-kuvioiden pinta-alojen kaavat on lisätty alla olevaan taulukkoon,

Kuvat

Kaava

Muuttujat

Suorakulmio

Pinta-ala = l × b
  • l on pituus
  • b on leveys

Neliö

Alue = a2

a on neliön sivu

Kolmio

Pinta-ala = 1/2 × bh
  • b on kanta
  • h on korkeus

Ympyrä

Pinta-ala = πr2

r on ympyrän säde

Trapetsoidi

Pinta-ala = 1/2×(a+b)h
  • a on ensimmäinen kanta
  • b on toinen kanta

Rombi

Pinta-ala = 1/2×d1×d2
  • d1on yksi diagonaali
  • d2on toinen lävistäjä

Suunnikas

Pinta-ala = b × h
  • b on kanta
  • h on korkeus

Ellipsi

Pinta-ala = πab
  • a on pääakselin säde
  • b on sivuakselin säde

Mitä ovat 3D-muodot?

3-D-muodot ovat muotoja, jotka piirretään 3-D-tiloihin. Niillä on 3 ulottuvuutta, jotka ovat niiden parametrit. Näiden muotojen pinta-ala riippuu 3D-muotojen pituudesta, leveydestä ja korkeudesta. Erilaisia ​​3-D-muotoja ovat kuutio, kuutio, sylinteri, kartio, pallo ja muut. Kolmiulotteisten muotojen pinta-ala on jaettu kahteen luokkaan, jotka ovat kaareva pinta-ala (Lateral Surface Area){CSA} ja kokonaispinta-ala (TSA). CSA on 3D-muotojen kaikkien kaarevien pintojen pinta-ala ja TSA on 3D-muotojen kaikkien pintojen pinta-ala.

3D-muotojen kaavan alue

Kolmiulotteisten muotojen pinta-ala on tila, jonka hahmon kaikki kasvot vievät. Se mitataan yksiköissä2. Pinta-alan SI-yksikkö on m2. The kuution pinta-ala , pinta-ala kuutio , alue sylinteri, ala kartio ja muut tulevat alueella 3D muotoja. Alla lisätty taulukko näyttää eri 3D-kuvioiden kaavat.

merkkijonotaulukon luominen javassa

Muodon alue

Pinta-ala

Parametrit

Kuution alue

6a2

a on reunan pituus

Cuboidin alue

2 (lb + lh + bh)
  • l on reunan pituus
  • b on reunan leveys
  • h on reunan korkeus

Kartion alue

πr(r + l)
  • r = pyöreän kannan säde
  • l = vino korkeus

Sylinterin alue

2π(r + h)
  • r = pyöreän kannan säde
  • h = sylinterin korkeus

Pallon alue

4πr2

r on pallon säde

Puolipallon alue

3πr2

r on pallonpuoliskon säde

Suorakaiteen muotoisen prisman pinta-ala

2 (wl + hl + hw)
  • l on reunan pituus
  • w on reunan leveys
  • h on reunan korkeus

Myös Tarkista

  • Alue- ja kehäkaavat
  • Pinta-alakaavat

Esimerkkejä aluekaavoista

Esimerkki 1: Etsi suorakulmion pinta-ala, jonka pituus on 5 cm ja leveys 2 cm.

Ratkaisu:

Annettu,

  • Suorakulmion pituus (l) = 5 cm
  • Suorakulmion (b) leveys = 2 cm

Suorakulmion pinta-ala (A) = l × b

A = 5 cm × 2 cm
= 10 cm2

Esimerkki 2: Etsi neliöpuiston alue, jonka sivu on 4 m.

Ratkaisu:

Annettu,

  • Neliön (a) sivu = 4 m

Neliön pinta-ala = a2
= (4)2= 16 m2

Näin ollen neliöpuiston pinta-ala on 16 m2

Esimerkki 3: Etsi pinta-ala kolmiomaisesta levystä, jonka korkeus on 6 cm ja pohja on 6 cm.

Ratkaisu:

Annettu,

  • Kolmion korkeus (h) = 6 cm
  • Kolmion (b) pohja = 8 cm

Kolmion pinta-ala(A) = 1/2(b × h)

A = 1/2(8 × 6)
= 48/2 = 24 cm2

Kolmiolevyn pinta-ala on 24 cm2

Esimerkki 4: Etsi ympyränmuotoisen kiekon pinta-ala, jonka säde on 1,4 cm.

Ratkaisu:

Annettu,

  • Ympyrän säde (r) = 1,4 cm

Ympyrän pinta-ala(A) = πr2

A = π(1,4)2
= 22/7(1.4)(1.4) = (4.4)(1.4)
= 6,16 cm2

Pyöreän kiekon pinta-ala on 6,16 cm2

Aluekaavojen UKK

Mitä ovat aluekaavat?

Pinta-alakaavat ovat kaavoja, joita käytetään minkä tahansa kuvion alueen löytämiseen. Sitä käytetään hahmon viemän tilan määrän selvittämiseen. Yleensä alue esitetään kirjaimella 'A'. ja mitataan yksiköissä2, eli cm2, m2, jne.

Mikä on Area Formula For Square?

Neliön pinta-alakaava on kaava neliön käyttämän tilan laskemiseksi. Kaava neliön pinta-alan laskemiseksi on,

Neliön alue = (sivu) 2

Mikä on suorakulmion aluekaava?

Suorakulmion pinta-alakaava on kaava, jolla lasketaan suorakulmion viemä tila. Kaava suorakulmion pinta-alan laskemiseksi on,

Suorakulmion pinta-ala = pituus × leveys

java avoin tiedosto

Mikä on kolmion pintakaava?

Kolmion pinta-alakaava on kaava, jolla lasketaan kolmion viemä tila. Kaava kolmion pinta-alan laskemiseksi on,

Kolmion pinta-ala = 1/2 (pohja × korkeus)

Mikä on Area Formula For Circle?

Ympyrän pinta-alakaava on kaava, jolla lasketaan ympyrän viemä tila. Kaava ympyrän pinta-alan laskemiseksi on,

Ympyrän pinta-ala = π(säde) 2

Mikä on nelikulmion pinta-alakaava?

Kaava nelikulmion pinta-alan laskemiseksi,

Nelisivun pinta-ala = 1/2 × lävistäjä 1 × Diagonaali 2

Mikä on kolmioprisman pintakaava?

Kolmioprisman alueen kaava on,

Kolmion muotoisen prisman pinta-ala = (jalustan kehä × prisman pituus) + 2 × pohjan pinta-ala

Mikä on monikulmion aluekaava?

Kaava monikulmion alueen laskemiseksi on,

Monikulmion pinta-ala = 1/2 × (kehä × apoteemi)

Mikä on suorakulmaisen kolmion aluekaava?

Suorakulmaisen kolmion alueen kaava on,

Suoran kolmion pinta-ala = 1/2 × kohtisuora × kanta

Mikä on Pentagonin aluekaava?

Pentagonin alueen kaava on,

Pentagonin pinta-ala = 1/2 × Kehä × Apoteemi