the Kosinifunktio tai cos Lyhyesti sanottuna toiminto on yksi kuudesta Trigonometriset funktiot trigonometrian perusta. Trigonometriassa kosini annetaan suorakulmaisen kolmion kantan ja hypotenuusan suhteena. Kosinifunktio esitetään muodossa Cos x, jossa x on kulma, jolle kosinisuhde lasketaan. Funktiolla voidaan sanoa, että x on kosinifunktion syöte tai toimialue.

Sitä käytetään laajasti monissa eri aiheissa, kuten fysiikassa, geometriassa ja tekniikassa, muun muassa yleensä hyödyntämällä sen jaksollista luonnetta. Sitä käytetään esimerkiksi määrittämään ääniaaltojen aaltolaatua, laskemaan sähkövirtaa tasopinnan läpi jne. Tässä artikkelissa opimme yksityiskohtaisesti siitä, mikä on kosinifunktio, verkkotunnus ja alue kosinifunktiosta, jaksosta ja kosinifunktion kaaviosta.

Sisällysluettelo

• Mikä on kosinifunktio?
• Cos yksikköympyrässä
• Kosinifunktiokaavio
• Kosinifunktion käänteisfunktio
• Kosinifunktio Calculusissa
• Cos-funktioiden identiteetit

Mikä on kosinifunktio?

Kosinifunktio on trigonometrinen funktio, joka on periaatteessa jaksollinen. Kosinifunktio ilmaistaan ​​muodossa cos x, jossa x on yksi suorakulmaisen kolmion terävistä kulmista. Kosinifunktio etsii emäksen ja hypotenuusan suhteen annetulle x:n arvolle. Kosinifunktio on lyhennetty nimellä cos(x) tai cos(θ), missä x on kulma radiaaneina ja theta θ on kulma astetta yleisesti. Kosinifunktio voidaan määrittää käyttämällä yksikköympyrää eli yksikkösäteen ympyrää, kuten näemme myöhemmin tässä artikkelissa. Se on luonteeltaan jaksollinen ja toistaa arvonsa jokaisen täydellisen kulmien kierron jälkeen. Karteesisella tasolla sitä voidaan kutsua hypotenuusan vektorikomponentiksi, joka on yhdensuuntainen x-akselin kanssa.

Kosinifunktion määritelmä

Kosinifunktio määritellään suorakulmaisessa kolmiossa kyseisen kulman vieressä olevan sivun pituuden ja hypotenuusan pituuden suhteena. Matemaattisesti kosinifunktio annetaan muodossa

Cos x = Cos θ = pohjan pituus/hypotenuusan pituus = b/h = OB/OA

missä x on kulma radiaaneina ja θ on vastaava kulma asteina.

Verkkotunnus ja Cos-toiminnon alue

Tiedämme, että funktiolle verkkoalue on sallitut tuloarvot ja alue on kyseisen syötteen tai toimialueen arvon lähtöarvo. Tästä syystä voimme olettaa, että funktio toimii kuten prosessori, joka ottaa syötteen, käsittelee sen ja antaa tietyn tulosteen. Cos-toiminnon toimialuetta ja aluetta käsitellään alla:

• Kosinifunktion alue: R eli kaikkien reaalilukujen joukko.
• Kosinifunktion alue: [-1, 1], eli lähtö vaihtelee kaikkien reaalilukujen välillä välillä -1 ja 1.

Kosinifunktion jakso

The toiminto on luonteeltaan jaksollinen, eli se toistaa itseään 2π:n tai 360°:n jälkeen. Toisin sanoen se toistaa itseään jokaisen täydellisen kierroksen jälkeen. Siten kosinifunktion jakso on täydellinen kierto tai 360° (tai 2π) kulma.

Kosinifunktion käänteisluku

Kosinifunktion käänteisluku tunnetaan nimellä sekantti toiminto tai sek lyhyesti. Matemaattisesti kosinifunktion käänteisluku annetaan muodossa

java ohjelmoinnin alkuluvut

sek(θ) = 1/cos(θ)

Sääntöjen mukaan Vastavuoroiset , jos kerromme Cos x:n Sec x:llä, tulo on aina 1.

Kosinifunktiokaavio

Kosinifunktion kuvaaja muistuttaa sinifunktion kuvaajaa sillä peruserolla, että kun x = 0 sinifunktion graafi kulkee origosta, kun taas x = 0:ssa kosinifunktion graafi kulkee pisteestä (0, 1) y-aixissa. Seuraavassa on kosinifunktion arvon kaavio eli y = cos x

Yllä käsitellyt ominaisuudet näkyvät kaaviossa kuten funktion jaksollinen luonne.

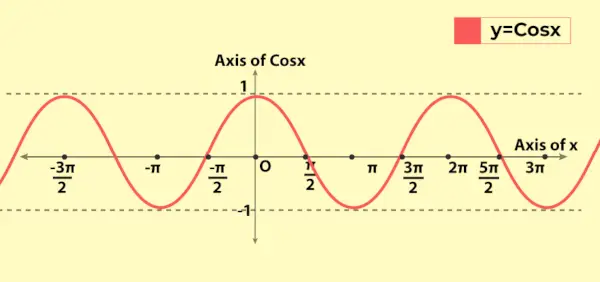
Kosinifunktion vaihtelu kaaviossa

Koska kosinifunktion alue on [-1, 1], se vaihtelee kaaviossa välillä -1:stä 1:een. Se osoittaa jaksollisen luonteensa, kun kaavio toistuu jokaisen pituuden 2π jälkeen x-akselilla. Tämä heijastaa sitä, että kosinifunktion jakso on 2π (tai 360°).

Cos yksikköympyrässä

Kosinifunktio voidaan määritellä yksikköympyrän avulla. Ymmärretään kuinka voimme määritellä kosinifunktion yksikköympyrän kannalta.

Tarkastellaan pisteen O ympäri pyörivää janaa OA, jossa O on suorakulmaisen tason origo. Siten OA:n rotaatio kuvaa yksikköympyrää (yksikkösäteen ympyrää), jonka keskipiste on origossa O ja piste A on aina tällä ympyrällä. Jos pudotamme kohtisuoran A:sta x-akselilla ja kutsumme leikkauspistettä B:ksi ja θ on kulma, jonka OA muodostaa x-akselin positiivisen suunnan kanssa, niin cos(θ) = hypotenuusan projektio x-akselilla -akseli = OB/|OA| = OB (koska |OA| = 1 yksikkö).

Huomaa, että suunta OB on tärkeä, kuten seuraavissa kuvissa näkyy. Vihreä segmentti ilmaisee cos(θ) pituuden/magnitudin ja nuoli suuntaa (+ve tai -ve)

Huomaa, että cos(θ):n arvo on positiivinen ensimmäiseen ja neljänteen neljännekseen kuuluvalle θ:lle, kun taas negatiivinen toiseen ja kolmanteen neljännekseen kuuluvalle θ:lle.

Kosinifunktion käänteisfunktio

Kosinifunktion käänteisarvo, joka tunnetaan nimellä kaari-kosinin funktio ja lyhennettynä arccos(x) tai cos ^-1 (x) määritellään seuraavasti

cos(x) = y

⇒ cos ^-1 (y) = x

Toimialue ja käänteisen kosinifunktion alue

Käänteisen kosinifunktion toimialue ja alue mainitaan alla:

• Käänteisen kosinifunktion toimialue: Kaikki reaaliluvut alueella [-1, 1]
• Käänteisen kosinifunktion alue: Kaikki reaaliluvut alueella [0, π]

Hyperbolinen kosinifunktio

Hyperboliset funktiot ovat analogisia ekvivalentteja trigonometriselle funktiolle, jonka algebrallinen lauseke on eksponentiaalisen funktion termeissä. Hyperbolinen kosinifunktio lyhennettynä cosh(x) missä x on hyperbolinen kulma on hyperbolisen geometrian käsite. Kuten (cos(x), sin(x)) edustaa yksikköympyrän pistettä, (cosh(x), sinh(x)) edustaa pistettä yksikköhyperbolissa eli xy = 1, jossa sinh(x) on hyperbolinen sinifunktio. Hyperbolisen cos-funktion algebrallinen laajennus on annettu muodossa

cosh(x) = (e ^x + ja ^-x )/2

Lisätiedot hyperbolisista funktioista eivät kuulu tämän artikkelin piiriin, mutta voit viitata niihin Tämä artikkeli .

Kosinifunktio Calculusissa

Matematiikan laskennan haara käsittelee eriyttäminen ja integrointi tietystä funktiosta. Toiminnon differentiointi on funktion muutosnopeus suhteessa riippumattomaan muuttujaan, kun taas integrointi on käänteinen differentiaatioprosessi, joka käsittelee funktion integraalin löytämistä, jonka derivaatta on olemassa.

Kosinifunktion johdannainen

The johdannainen kosinifunktion on yhtä suuri kuin sinifunktion negatiivinen. Matemaattisesti

d(cos(x))/dx = -sin(x)

Kosinifunktion integrointi

The epämääräinen integraali kosinifunktio on yhtä suuri kuin sinifunktio. Matemaattisesti -

∫cos(x)dx = sin(x) + C, missä C on integroinnin vakio.

Sini- ja kosinifunktiot

Seuraava kaavio edustaa keskeistä eroa sekä sini- että kosinifunktion välillä:

Ero sini- ja kosinifunktioiden välillä

Seuraavassa taulukossa on lueteltu erot sini- ja kosinifunktion välillä –

Cos-arvotaulukko

Seuraavassa taulukossa on kosinifunktion arvot joillekin yhteisille kulmille suorakulmaisen tason ensimmäisessä kvadrantissa –

Voimme helposti laskea muiden yleisten kulmien, kuten 15°, 75°, 195°, -15° jne. arvot käyttämällä näitä arvoja käyttämällä kaavoja cos (x + y) ja cos (x - y), jotka kuvataan myöhemmin tässä. artikla.

Tarkistaa, Trigonometrinen taulukko

Cos-funktioiden identiteetit

Alla mainitaan kosinifunktioon liittyvät trigonometriset perusidentiteetit:

• ilman²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/s(x)
• cos 2x = cos²x – synti²x = 1 – 2sin²x = 2cos²x – 1 = (1 – ruskea²x/1 + rusketus²x)
• cos 3x = 4cos³x – 3cos x

Aiheeseen liittyvät artikkelit

• Trigonometristen funktioiden erottelu
• Käänteiset trigonometriset funktiot
• Käänteiset trigin johdannaiset

Ratkaistiin esimerkkejä kosinifunktiosta

Tässä on joitain ratkaistuja esimerkkejä, jotka auttavat sinua ymmärtämään paremmin kosinifunktion käsitteen.

Esimerkki 1: Mitkä ovat kosinifunktion maksimi- ja minimiarvot?

Ratkaisu:

Kosinifunktion maksimiarvo on 1 kulmassa 0° ja 180°, kun taas funktion minimiarvo on -1 kulmassa 180°.

Esimerkki 2: Missä kulmassa (kulmissa) alueella [0, 360] kosinifunktion arvo on 0?

Ratkaisu:

Kosinifunktion arvo on 0 kulmissa 90° ja 270°.

Esimerkki 3: Millä neljänneksillä kosinifunktion arvo on negatiivinen?

Ratkaisu:

Kosinifunktio on negatiivinen II^ndja III^rdkvadrantit.

Esimerkki 4: Laske cos (45°) arvo.

Ratkaisu:

csv-tiedoston lukeminen javassa

Yllä annetun identiteetin 4 mukaisesti cos(-x) = cos(x).

Siksi cos(-45°) = cos(45°) = 1/√2

Esimerkki 5: Laske cos(15°) arvo.

Ratkaisu:

Käyttämällä yllä annettua identiteettiä 3 -

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Esimerkki 6: Mikä on cos ^-1 (1/2) alueella [0,π]?

Ratkaisu:

Anna cos^-1(1/2) = y.

Siksi cos(y) = 1/2 ⇒ y = π/3 yllä annetulla alueella.

Siksi vastaus on π/3.

Esimerkki 7: Mikä on cos(-15°):n arvo?

Ratkaisu:

Käyttämällä yllä annettua identiteettiä 3 -

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Vaihtoehtoisesti voimme myös käyttää identiteettiä cos(-x) = cos(x) ja käyttää esimerkissä 5 laskettua cos(15°):n arvoa.

Esimerkki 8: Laske kosinifunktion kaavion alla oleva pinta-ala x = 0 - x = π/2.

Ratkaisu:

Annettu pinta-ala voidaan laskea ratkaisemalla seuraava kiinteä integraali -

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Siksi vastaus on 1 neliöyksikkö.

Esimerkki 9: Jos cos(x) = π/3, etsi cos(3x):n arvo (desimaalimuodossa kahden desimaalin tarkkuudella).

Ratkaisu:

Identiteettiä käyttämällä – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Esimerkki 10: Etsi cos(120°) arvo.

Ratkaisu:

Cos(2x) identiteetin käyttäminen

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1-2⨉(√3/2)²= 1 – 3/2 = -1/2

Harjoituskysymykset: Cos-funktiot

Q1. Millä kaavalla lasketaan kulman cos suorakulmaisessa kolmiossa?

Q2. Mikä on cosin geometrinen tulkinta karteesisella tasolla?

Q3. Laske cos(120°) arvo.

Q4. Etsi cos:n arvo ^-1 (√3/2) alueella [π, 2π].

Q5. Jos pylväs heittää maahan samanpituisen varjon, selvitä auringon kulma maahan nähden, jos aurinko on itään.

Yhteenveto – kosinifunktio

Kosinifunktio, jota kutsutaan nimellä cos(x), on perustavanlaatuinen trigonometrinen funktio, joka määritellään kannan ja hypotenuusan suhteeksi suorakulmaisessa kolmiossa ja on jaksollisen luonteensa vuoksi olennainen useilla aloilla, kuten fysiikassa, tekniikassa ja geometriassa. , joka on tärkeä aaltokäyttäytymisen mallintamisessa. Sillä on kaikkien reaalilukujen verkkoalue ja alue -1:stä 1:een, toistaen syklinsä joka 2 Pi radiaania tai 360 astetta, mikä käy ilmi sen aaltomaisesta kaaviosta, joka alkaa arvosta (0,1). Laskennassa cos(x):n derivaatta on − sin( x ), ja sen integraali tuottaa sin( x )+ C , jossa C integroinnin vakiona. Tämä toiminto ulottuu myös hyperbolisiin muotoihin, kuten cosh(x), parantaen sen käyttöä erilaisissa matemaattisissa yhteyksissä ja ratkaisuissa, mukaan lukien aaltolaskelmat ja värähtelyt fysikaalisissa järjestelmissä.

Kosinifunktio: UKK

1. Mikä on kosinifunktio?

Kosinifunktio on yksi tärkeimmistä trigonometrisista funktioista. Se määritellään suorakulmaisessa kolmiossa kyseisen kulman vieressä olevan sivun pituuden ja hypotenuusan pituuden suhteena.

2. Ovatko Cos ja Cosini samat trigonometriassa?

Joo. cos on kosinifunktion lyhenne/lyhenne.

3. Mikä on Cos-funktion alue?

Cos- tai kosinifunktion alue on kaikki reaaliluvut, jotka vaihtelevat -1:stä 1:een, eli [-1,1].

4. Mikä on Cos-funktion toimialue?

Cos- tai kosinifunktion toimialue on kaikkien reaalilukujen ser, eli R .

5. Mikä on kosinifunktion enimmäisarvo?

Kosinifunktion maksimiarvo on 1 kaikille kulmille, jotka vastaavat 0° tai 360°.

6. Mikä on kosinifunktion vähimmäisarvo?

Kosinifunktion minimiarvo on -1 kaikille kulmille, jotka vastaavat 180°.

7. Kuinka löytää Cos(-x)-arvo?

Cos(-x):n arvo voidaan laskea laskemalla cos(x):n arvo seuraavan identiteetin olemassaolon vuoksi: cos(-x) = cos(x).

8. Miten kosinifunktio piirretään?

Piirtääksesi kosinifunktion kaavion suorakulmaiselle tasolle, katso, että x-akseli edustaa kulmia radiaaneina (tai asteina) ja y-akseli edustaa kosinifunktion arvoja vastaavalle kulman x-akselilla. Nyt,

• Vaihe 1: Ota x-akselin osajoukko, jolle haluat piirtää kaavion.
• Vaihe 2: Jaa tällä alueella oleva x-akseli tasaetäisyydellä oleviin pisteisiin (eli kaikkien alipisteiden välillä on yhtä suuri tila). Huomaa, että mitä enemmän jakoja on, sitä suurempi on tuloksena olevan graafin tarkkuus.
• Vaihe 3: Merkitse jokaiselle näistä alipisteistä x piste (x, cos(x)) kuvaajaan.
• Vaihe 4: Yhdistä kaikki merkityt pisteet saadaksesi kosinifunktion kaavion (valitsemasi x-akselin osajoukolle).

9. Kuinka löytää kosinifunktion jakso?

Kosinifunktion jakso viittaa minimiarvoalueeseen, jonka jälkeen funktio alkaa toistaa itseään. Tiedämme, että kosinifunktio toistaa itseään jokaisen täydellisen kierroksen jälkeen, mikä tarkoittaa 2π radiaania. Siksi kosinifunktion jakso on 2π radiaania tai 360°.

10. Mikä on kosinifunktion amplitudi?

Kosinifunktion amplitudi viittaa funktion arvon maksimisiirtoon keskimääräisestä sijainnista eli x-akselista. Kosinifunktion amplitudi on 1, koska suurin siirtymä on 1 (arvoille -1 ja 1 180 ja 0 asteessa. Huomaa, että kosinifunktion alue on [-amplitudi, amplitudi].