A Toiminto matematiikassa on erityinen suhde syöttöarvojen joukon ja lähtöarvojen joukon välillä. Functionissa jokainen tuloarvo antaa tietyn lähtöarvon. Esitämme funktion matematiikassa muodossa, y = f(x) missä x on syöttöarvo ja jokaiselle x saamme lähtöarvon muodossa y.

Tässä artikkelissa opimme, matematiikan funktiot, niiden eri tyypit, esimerkit ja muut yksityiskohtaisesti.

Sisällysluettelo

• Mikä on funktio matematiikassa?
• Funktion määritelmä matematiikassa
• Toiminnot Esimerkkejä
• Tehtävän ehto
• Funktioiden esitys matematiikassa
• Toiminnon tunnistus
• Toimintojen tyypit
• Mikä on funktio algebrassa?
• Toimialue ja toiminnon alue
• Toimintojen kokoonpano
• Funktioiden algebra
• Mikä on funktio kaaviossa?
• Graafiset funktiot
• Yhteiset toiminnot
• Funktioiden sovellukset
• Esimerkkejä toiminnasta
• Harjoittele ongelmia siitä, mikä on toiminto

Mikä on funktio matematiikassa?

Matematiikan funktio on a suhde annettujen joukkojen syötearvojen (domain) ja lähtöarvojen (alue) välillä siten, että kahta muuttujaa domain-joukoista ei ole linkitetty samaan vaihteluvälijoukon muuttujaan. Yksinkertainen esimerkki funktiosta matematiikassa on f(x) = 2x, joka määritellään parametrilla R→R, tässä mikä tahansa alueen muuttuja liittyy vain yhteen muuttujaan alueella.

Matematiikan funktiolla on toimialue, koodialue ja alue. Toimialue on kaikkien x:n mahdollisten arvojen joukko ja funktion alue on kaikkien y:n lähtöarvojen joukko. Alue on funktion koodialueen osajoukko. Voidaan myös sanoa, että funktio matematiikassa on relaatio, jolla on ainutlaatuinen tulos, eikä kahdella tuloarvolla ole samanlaista lähtöä funktiossa, kuten relaatiossa.

Funktion määritelmä matematiikassa

Funktio on erityinen relaatio tai menetelmä, joka yhdistää jokaisen joukon A jäsenen joukon B yksilölliseen jäseneen määritellyn suhteen kautta. Joukkoa A kutsutaan toimialueeksi ja joukkoa B funktion rinnakkaisalueeksi. Matematiikassa funktio joukosta A joukkoon B määritellään seuraavasti:

f = ∀ a ∈ A, b ∈ B

Jokainen funktio on relaatio, mutta jokainen relaatio ei ole funktio. Kriteerit minkä tahansa suhteen katsomiselle funktiona, koska funktiossa jokaisella joukon A elementillä on vain yksi kuva joukossa B, kun taas suhteessa joukon A elementillä voi olla useampi kuin yksi kuva joukossa B.

Määritämme funktiot matematiikassa ei-tyhjästä joukosta A ei-tyhjään joukkoon B siten, että

(a, b) ∈ f, niin f(a) = b

minne soitimme b kuvana a määritellään suhteen alla f .

Jokainen elementti 'a' sarjalla A on ainutlaatuinen kuva ' b ' joukossa B, niin se on funktio.

Toiminnot Esimerkkejä

Matematiikan funktio f määritellään seuraavasti, y = f(x) missä x on syötearvo, ja jokaiselle x:n syötearvolle saadaan yksilöllinen arvo y. Useita esimerkkejä matemaattisista funktioista, jotka on määritelty kohdassa R → R, ovat

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+3 jne

Tehtävän ehto

Jokaiselle kahdelle ei-tyhjälle joukolle A ja B, funktio f: A→B tarkoittaa sitä f on funktio A:sta B:hen, jossa A on verkkotunnus ja B on yhteisverkkotunnus.

Jokaiselle alkiolle a ∈ A on ainutlaatuinen alkio, b ∈ B, niin että (a,b) ∈ f. Yksilöllinen elementti b, joka liittyy a:han, merkitään f(a):lla ja luetaan a:n f:ksi. Tämä voidaan ymmärtää paremmin alla olevasta kuvasta:

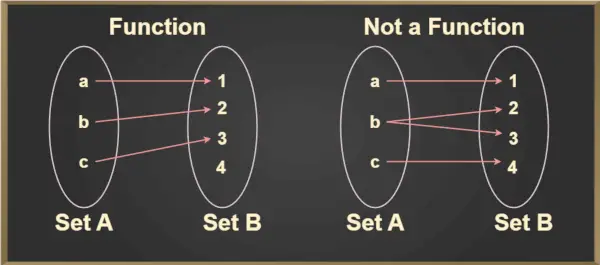
Pystyviivatesti

Pystyviivatestiä käytetään määrittämään, onko käyrä funktio vai ei. Jos jokin käyrä leikkaa pystysuoran viivan useammassa kuin yhdessä pisteessä, käyrä ei ole funktio.

Funktioiden esitys matematiikassa

Edustamme funktiota matematiikassa mm.

y = f(x) = x + 3

Tässä x:n arvojen joukko on funktion toimialue ja y:n lähtöarvojen joukko on funktion yhteisalue. Tässä funktio on määritelty kaikille reaaliluvuille, koska se antaa jokaiselle x:lle ainutlaatuisen arvon, mutta jokaiselle x:n arvolle ei aina ole mahdollista saada lähtöä, jolloin määritämme funktion kahdessa osassa, tämä voidaan ymmärtää

muuntaa merkkijonon päivämäärä

• f(x) = 1/(x – 2), missä x ≠ 2
• f(x) = x²missä x ∈ {R}

Voimme määritellä funktion matematiikassa koneeksi, joka ottaa jonkin verran syötettä ja antaa ainutlaatuisen tulosteen. Funktio f(x) = x²määritellään alla seuraavasti,

Voimme esittää funktion matematiikassa kolmella menetelmällä:

• Sarja tilattuja pareja
• Taulukkolomake
• Graafinen muoto

Jos esimerkiksi edustamme funktiota muodossa, f(x) = x³

Toinen tapa edustaa samaa funktiota on sarja tilattuja pareja kuten,

f = {(1,1), (2,8), (3,27)}

Yllä mainitussa joukossa funktion alue on D = {1, 2, 3} ja funktion alue on R = {1, 8, 27}

Toiminnon tunnistus

Funktio luokitellaan matematiikassa erityiseksi relaatiotyypiksi. Toiminnon tunnistamiseen voidaan käyttää seuraavia sääntöjä:

• Suhde, jossa jokainen yksilölliseen ulostuloon yhdistetty tulo on funktio. Tämä kutsui yksi yhteen funktiota.
• Suhde, jossa kaksi tuloa (esikuvaa) yhdistettynä yhteen lähtöön, on myös funktio. Tämä on monta toimintoa yhteen.
• Suhde, jossa yksi tulo on yhdistetty kahteen eri lähtöön, ei ole funktio.
• Suhde, jossa monet tulot on kartoitettu useisiin lähtöihin noudattaen mitään tiettyä sääntöä, ei ole funktio.

Toimintojen tyypit

Eri Toimintojen tyypit Niitä käytetään ratkaisemaan erilaisia ​​matemaattisia ongelmia, jotka liittyvät erityisesti käyriin ja yhtälöihin. Matematiikassa on kolme päätyyppistä funktiota, jotka perustuvat elementtien kartoitukseen joukosta A joukkoon B.

Injektiotoiminto tai One to One Function

Toimintoa, jossa jokaisella toimialueen elementillä on erillinen kuva koodialueella, kutsutaan nimellä Injektiivinen tai Yksi-yhteen-toiminto .

f: A → B:n sanotaan olevan yksi yhteen tai injektiivinen, jos A:n eri elementtien kuvat kohdassa f ovat erilaisia, ts.

fa ₁ ) = b ₁ , f(a ₂ ) = b ₂

missä₁, a₂∈ A ja b₁, b₂∈ B

Surjektiiviset funktiot tai Onto-funktio

Surjektiivinen funktio on toiminto, jossa jokaisella koodialueen elementillä on esikuva toimialueella. Sitä kutsutaan myös Toimintoon mikä tarkoittaa, että jokainen koodidomeenin elementti liittyy alueen jokaiseen elementtiin. Millään koodialueen elementillä ei saa olla tyhjää suhdetta. Koodomainin ja alueen elementtien lukumäärä on sama.

f: A → B:n sanotaan olevan päällä, jos jokainen B:n elementti on jonkin A:n elementin kuva kohdassa f, ts. jokaiselle b ϵ B:lle, A:ssa on elementti 'a' siten, että f(a) = b.

Bijektiivinen toiminto

Jos funktiolla on sekä injektiivinen (yksi yhteen) että surjektiivinen (onto-funktio) ominaisuuksia, funktiota kutsutaan Bijektiivinen toiminto . Bijective Functionissa verkkoalueen jokainen elementti liittyy koodialueen jokaiseen elementtiin, ja siellä on myös yksi-yhteen-suhde. Tämä tarkoittaa, että koodialueen ja alueen elementtien lukumäärä on sama eikä millään elementillä toimialueen tai koodialueen elementillä ole tyhjä suhde.

Lähtöarvojen perusteella funktiot luokitellaan parittomiksi ja parillisiksi funktioiksi. Katsotaanpa niitä

Parittomat toiminnot

Pariton funktio on eräänlainen funktio, joka osoittaa symmetriaa origon suhteen. Tarkemmin sanottuna, jos f(x) on pariton funktio, se osoittaa, että f(-x) = -f(x)

Jopa toiminto

Parillinen funktio on eräänlainen funktio, joka osoittaa symmetriaa y-akselin suhteen. Tarkemmin sanottuna, jos f(x) on parillinen funktio, se osoittaa, että f(-x) = f(x)

raja css:llä

Mikä on funktio algebrassa?

Toiminto sisään algebra on yhtälö, jolle mikä tahansa x, joka voidaan laittaa yhtälöön, tuottaa täsmälleen yhden tulosteen, kuten y:n, yhtälöstä. Se esitetään muodossa y = f(x), missä x on riippumaton muuttuja ja y on riippuvainen muuttuja.

Esimerkiksi:

• y = 2x + 1
• y = 3x – 2
• y = 4v
• y = 5/x

Toimialue ja toiminnon alue

Verkkotunnus ja alue funktion tulo- ja lähtöarvot ovat vastaavasti. Oletetaan esimerkiksi, että meillä on funktio f(x) = x². Tässä voimme ottaa kaiken reaaliluvun x:n syöttöarvona ja tulos on aina positiivinen reaaliluku. Siksi sen verkkoalue on asetettu kaikista reaaliluvuista, jotka esitetään muodossa R, kun taas sen alue on joukko positiivisia reaalilukuja, jotka esitetään muodossa R⁺

Toimintojen kokoonpano

Jos f: A → B ja g: B→ C ovat kaksi funktiota. Sitten f:n ja g:n koostumus merkitään f(g):llä ja se määritellään funktioksi sumu = f(g(x)) x ∈ A:lle.

Otetaan kaksi funktiota f(x) = x + 3 ja g(x) = 2x²

sumu = f(g(x))

⇒ sumu = f(2x²)

⇒ hammas = 2x²+ 3

Lisätietoja, Toiminnan kokoonpano

Funktioiden algebra

Funktioiden algebra sisältää algebralliset operaatiot, jotka suoritetaan kahden funktion välillä. Algebrallinen operaatio kahdelle funktiolle f(x) ja g(x), jotka on määritelty x:n todellisella arvolla, mainitaan alla:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Sillä k on reaaliluku}
• (f/g)(x) = f(x)/g(x); {G(x) ≠ 0}

Mikä on funktio kaaviossa?

Funktio voidaan helposti esittää kaaviossa. Mikä tahansa kaaviossa oleva funktio edustaa käyrää (mukaan lukien suora) x-y-tasossa, joka on kartoitettu sen tulo- ja vastaaville lähtöarvoille.

Kun haluat piirtää funktion, etsi ensin joitain funktiossa olevia pisteitä ja yhdistä sitten nämä pisteet funktion paikan mukaan. Esimerkiksi funktion (suoran) kuvaajaksi f(x) = y = 5x – 2 tarvitsemme jonkin pisteen kuvaajasta. Löytääksemme pisteen pisteen kaaviosta otamme ensin x:n satunnaiset arvot ja etsimme sitten niitä vastaavat y:n arvot, kuten

f(x) = y = 5x-2

jos x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

jos x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

jos x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Nyt yhdistämällä nämä pisteet saadaan funktion y = 5x – 2 kuvaaja

Graafiset funktiot

Kun tiedät x:n arvot, funktio f(x) voidaan esittää kuvaajassa. Koska y = f(x), voimme löytää y:n liittyvän arvon aloittamalla x:n arvoista. Tämän seurauksena voimme piirtää graafin koordinaattitasoon käyttämällä x- ja y-arvoja. Harkitse seuraavaa skenaariota:

Oletetaan, että y = x + 3

Kun x = 0, y = 3

Samalla lailla,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Tämän seurauksena voimme piirtää funktion x + 3 kaavion käyttämällä näitä arvoja.

Yhteiset toiminnot

Joitakin matematiikassa yleisesti käytettyjä funktioita käsitellään alla:

Todellinen toiminto

Todellinen toiminto matematiikassa viittaa funktioon, jonka toimialue ja alue ovat reaalilukujen (merkitty ℝ) osajoukkoja. Yksinkertaisemmin sanottuna reaalifunktio on matemaattinen sääntö tai suhde, joka määrittää reaaliluvun arvon jokaiselle reaaliluvun syötölle.

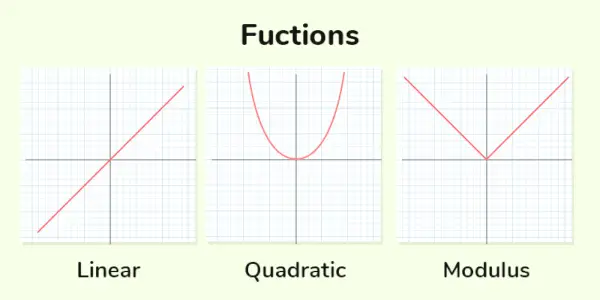
Todelliset toiminnot

Polynomifunktio

Funktiota, jossa algebrallisten muuttujien eksponentit ovat ei-negatiivisia kokonaislukuja kutsutaan Polynomifunktio . Jos muuttujan potenssi on 1, sitä kutsutaan lineaarifunktioksi, jos potenssi on 2, sitä kutsutaan neliöfunktioksi ja jos potenssi on 3, sitä kutsutaan kuutiofunktioksi. Alla mainitaan muutamia esimerkkejä polynomifunktioista:

• y = x²
• y = 2x + 3
• y = 3x³

Polynomifunktio voidaan edelleen luokitella seuraaviin tyyppeihin:

satunnaisarvogeneraattori javassa

Lineaarinen funktio : Lineaarinen funktio on funktio, jossa muuttujan maksimiteho on 1. Yleinen muoto Lineaarinen funktio On y = mx + c

Neliöllinen funktio : Neliöfunktiot ovat ne, joissa muuttujan maksimiteho on 2. Yleinen muoto neliöfunktio On, kirves ² + bx + c = 0

Kuutiofunktio : Kuutiofunktio on ne, joissa muuttujan maksimiteho on 3. Yleistä Kuutiofunktion muoto annetaan muodossa kirves ³ + bx ² + cx + d = 0

Käänteinen funktio

Käänteinen funktio on funktio, joka sisältää toisen funktion käänteisarvon. Oletetaan, että meillä on funktio y = f(x), niin sen käänteisfunktio on x = f^-1(y). Kohdassa y = f(x) alue on x ja alue on y, kun taas tapauksessa x = f^-1(y), toimialue on y ja alue on x. Näin ollen voidaan sanoa, että alkuperäisen funktion alue on sen käänteisfunktion alue ja alkuperäisen funktion alue on alkuperäisen funktion alue. Joitakin esimerkkejä käänteisfunktioista ovat,

• y = niin^-1(x)
• y = x^-1

Aluetoiminto

Pinta-alafunktio viittaa tyypillisesti matemaattiseen funktioon, joka laskee geometrisen muodon tai alueen alueen. Aluefunktio ottaa syötteeksi yhden tai useamman parametrin ja palauttaa vastaavan muodon alueen. Joitakin alueen toimintoja käsitellään alla:

Ympyrätoiminnon alue : Ympyrän alue (A) on säteensä (r) funktio siten, että

A = πr ²

Kolmiofunktion alue : Kolmion alue (A) on pohjan (b) ja korkeuden (h) funktio siten, että

A = (bh)/2

Eksponentti funktio

Eksponentti funktio on se, joka esitetään muodossa f(x) = e^x. Sitä käytetään usein osoittamaan nopeaa kasvua tai rappeutumista.

Logaritminen funktio

Logaritminen funktio on matemaattinen funktio, joka edustaa eksponentioinnin käänteistä toimintaa. Se esitetään muodossa f(x) = log x.

Kattotoiminto

Kattotoiminto , jota merkitään ⌈x⌉, pyöristää reaaliluvun x ylöspäin lähimpään kokonaislukuun, joka on suurempi tai yhtä suuri kuin x. Toisin sanoen se löytää pienimmän kokonaisluvun, joka on suurempi tai yhtä suuri kuin x.

harhaa ja varianssia

Lattiatoiminto

Lattiafunktio, jota merkitään ⌊x⌋, pyöristää reaaliluvun x alaspäin lähimpään kokonaislukuun, joka on pienempi tai yhtä suuri kuin x. Toisin sanoen se löytää suurimman kokonaisluvun, joka on pienempi tai yhtä suuri kuin x.

Moduulitoiminto

Moduulitoiminto , joka tunnetaan myös itseisarvofunktiona, palauttaa reaaliluvun suuruuden tai koon sen etumerkistä riippumatta. Moduulifunktio on merkitty ∣x∣, missä x on syötearvo.

Signum-toiminto

Signum-toiminto , joka tunnetaan myös etumerkkifunktiona tai merkkifunktiona, on matemaattinen funktio, joka palauttaa reaaliluvun etumerkin. Se osoittaa, onko luku positiivinen, negatiivinen vai nolla.

Trigonometriset funktiot

Trigonometriset funktiot ovat matemaattisia funktioita, jotka yhdistävät suorakulmaisen kolmion kulmat sen sivujen pituuksiin. Kuusi ensisijaista trigonometrista funktiota ovat sini (sini), kosini (cos), tangentti (tan), kosekantti (cosec), sekantti (sec) ja kotangentti (cot).

Monimutkaiset toiminnot

Mitä tahansa funktiota, jossa syötemuuttujat ovat kompleksisia funktioita, kutsutaan kompleksifunktioiksi. Kompleksiluku on luku, joka voidaan piirtää kompleksitasolla. Jonkin sisällä kompleksiluku meillä on reaaliluku ja imaginaariluku. Kompleksiluku(z) esitetään muodossa, z= x + iy ja kompleksifunktio esitetään muodossa, f(z) = P(x, y) + iQ(x, y)

Funktioiden sovellukset

Kun sanomme, että muuttuva suure y on muuttuvan suuren x funktio, osoitamme, että y on riippuvainen x:stä ja että y:n arvo määräytyy x:n arvon perusteella. Tämä riippuvuus voidaan ilmaista seuraavasti: f = y (x).

• Ympyrän säteen avulla voidaan laskea ympyrän pinta-ala. Säde r vaikuttaa alueeseen A. Ilmoitamme, että A on r:n funktio funktioiden matemaattisessa kielessä. Voimme kirjoittaa A = f(r) =π×r²
• Pallon tilavuus V on sen säteen funktio. V = f(r) = 4/3 × r³tarkoittaa V:n riippuvuutta r:stä.
• Voima on kiinteämassaisen m kappaleen kiihtyvyyden funktio. F = g(a) = m×a.

Ihmiset lukevat myös:

• Suhde ja toiminta
  
• Toimialue ja trigonometristen funktioiden alue
• Toiminnon alue
• Hyperbolinen toiminto

Esimerkkejä toiminnasta

Esimerkki 1: Kahdelle funktiolle f ja g määritellään seuraavasti: f(x) = x ² ja g(x) = ln(2x). Etsi yhdistelmäfunktio (gof )( x )

Ratkaisu:

Annettu:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Siten (gof)(x) = 2 ln(√2x)

Esimerkki 2: Etsi funktion g(t)= 6t tulos ² + 5 klo

• (i) t = 0
• (ii) t = 2

Ratkaisu:

annettu toiminto,

g(t) = 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Esimerkki 3: Suorakulmion pituus on viisi kertaa sen leveys, ilmaise suorakulmion pinta-ala sen pituuden funktiona.

Ratkaisu:

Olkoon suorakulmion pituus l ja suorakulmion leveys on, b

Nyt,

• b = l/5

Suorakulmion pinta-ala(A) = l × l/5 = l²/5

Siten suorakulmion pinta-ala sen pituuden funktiona on,

A(l) = l ² /5

Harjoittele ongelmia siitä, mikä on toiminto

1. Annettu funktio f(x)=3x+5

• Etsi f(2)
• Etsi f(−1)
• Määritä funktion toimialue ja alue.

2. Annettu funktio g(x)=x ² – 4x + 3

• Etsi funktion juuret.
• Etsi g(3) ja g(0).
• Määritä funktion kärki.

3. Annettu kaksi funktiota f(x)=x + 2 ja h(x)=2x – 3

• Etsi yhdistelmäfunktio (f ∘ h) (x)
• Arvioi (f ∘ h)(2)

Yhteenveto – Mikä on toiminto

Matematiikassa funktio on erityinen suhde tuloarvojen (domain) ja lähtöarvojen (alue) välillä, jossa jokaiseen tuloon liittyy yksilöllinen tulos. Esitettynä muodossa y = f(x), funktioilla on erityisiä ominaisuuksia ja ne voidaan visualisoida järjestetyillä pareilla, taulukoilla tai kaavioilla. Ne ovat välttämättömiä erilaisissa matemaattisissa ongelmissa, ja niitä on eri tyyppejä, mukaan lukien injektiivinen (yksi yhteen), surjektiivinen (onto) ja bijektiivi (molemmat). Funktiot voidaan testata pystyviivatestillä, ja ne luokitellaan edelleen polynomi-, käänteis-, eksponentti-, logaritmis- ja trigonometrisiin funktioihin. Toimintojen ymmärtäminen edellyttää niiden toimialueen, alueen ja niitä määrittelevien sääntöjen tunnistamista. Esimerkkejä ovat yksinkertaiset lineaarifunktiot, kuten y = 2x + 1 ja monimutkaiset funktioiden koostumukset. Funktioilla on ratkaiseva rooli algebrassa, geometriassa ja laskennassa, ja ne auttavat matemaattisten suhteiden ja reaalimaailman ilmiöiden esittämisessä ja analysoinnissa.

Usein kysytyt kysymykset aiheesta Mikä on toiminto

Mikä on funktion määritelmä?

Joukkoon A määritettyä relaatiota f toiseen joukkoon B kutsutaan matematiikassa funktioksi, jos jokaisella A:n arvolla on yksilöllinen arvo joukossa B.

np.linspace

Kuinka kirjoittaa funktio matematiikassa?

Funktion f matematiikassa esitetään muodossa f: A → B ja määritellään seuraavasti: f(x) = x + 2. Tässä jokaiselle x:n yksilölliselle arvolle meillä on yksilöllinen arvo y.

Kuinka muuttaa funktio?

Voimme helposti muuttaa funktion muihin funktioihin suorittamalla funktiolle algebrallisia perusoperaatioita. Toiminnon eri muunnokset ovat heijastus, translaatio, kierto jne.

Mikä on rationaalinen funktio?

Murto-osafunktiota, jossa osoittaja ja nimittäjä ovat polynomifunktioita, kutsutaan rationaaliseksi funktioksi. Joitakin esimerkkejä rationaalisista funktioista ovat mm.

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), jne.

Mikä on lineaarinen funktio?

Algebrallista funktiota, jossa jokainen funktion termi on joko vakio tai jonka potenssi on yksi, kutsutaan lineaarifunktioksi. Joitakin esimerkkejä lineaarisista funktioista ovat

• f(x) = 2x + 3
• g(x) = x – 5 jne.

Mitä ovat funktion verkkoalue ja koodialue?

Jos määritämme funktion seuraavasti, y = f(x). Tällöin x:n alue on kaikki x:n arvot, joille y johtaa yksilölliseen arvoon. Ja y:n yhteisverkkoalue on joukko y:n kaikkia arvoja jokaiselle x:n arvolle.

Miten tunnistat funktion matematiikassa?

Jos jollakin relaatiossa olevan toimialueen syötearvolla (x) on useampi kuin yksi kuva (y), nämä relaatiot eivät voi koskaan olla funktio. Joten jos x:n arvo toistuu järjestetyssä parissa, se ei ole koskaan funktio.