Vaakaviivat määritellään viivoiksi, jotka ovat yhdensuuntaisia horisontin tai maan kanssa, mistä johtuu nimi vaakaviiva . Vaakaviivalla on nollakaltevuus, eli näiden viivojen kaltevuuskulma on nolla astetta. Jos vaakaviivat piirretään suorakulmaisille tasoille, ne tekevät leikkauspisteen vain y-akselia pitkin, koska ne ovat aina yhdensuuntaisia x-akselin kanssa eivätkä koskaan leikkaa sitä.
Tässä artikkelissa opimme yksityiskohtaisesti vaakaviivasta, sen ominaisuuksista, vaakaviivan kaltevuudesta, vaakaviivan yhtälöstä, vaakaviivoista liittyvistä esimerkeistä ja usein kysytyistä kysymyksistä ja muista.
Sisällysluettelo
- Vaakaviivan määritelmä
- Vaakaviivan kaltevuus
- Vaakaviivan piirtäminen
- Vaakaviivayhtälö
- Vaakaviivatesti
- Vaaka- ja pystysuorat viivat
- Erot pystysuorien ja vaakasuuntaisten viivojen välillä
- Lyhyt huomautus vaakaviivasta
- Esimerkkejä vaakasuuntaisista viivoista
Vaakaviivan määritelmä
Tiedämme, että viiva on suora polku, joka yhdistää kaksi tai useampia pistettä ja kulkee äärettömään. Siten määrittelemme vaakaviivat viivoiksi, jotka ovat yhdensuuntaisia maan tai horisontin kanssa ja ovat vakiokorkeudella maasta.
Jos piirrämme nämä suorat suorakulmaiseen järjestelmään, nämä suorat ovat suoria, joilla ei ole leikkauspistettä x-akselilla mutta joilla on leikkauspiste y-akselilla. Vaakasuuntaisilla viivoilla on nollakaltevuus, eli niillä on nollakulma x-akselin tai maan kanssa.
Vaakaviivat muodostavat perustan erilaisille kohteille, muodoille ja kuvioille, joita tutkimme geometriassa. Oletetaan, että meidän on piirrettävä suorakulmio, neliö, kolmio, trapetsi jne., niin näiden lukujen pohja on enimmäkseen vaakasuorat viivat. Havaitsemme vaakasuuntaisia valheita myös tosielämässä, sillä myös lattian ja huoneiden katolla olevat viivat, portaiden pohjat jne. tehdään vaakasuorista viivoista.
Nämä viivat tunnetaan myös nukkumislinjoina, koska niillä ei ole pystysuuntaista liikettä ja ne pysyvät aina tasaisella korkeudella maasta. Alla lisätty kuva näyttää vaakaviivan.
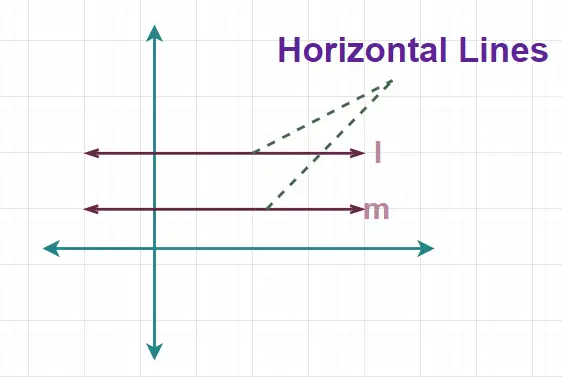
Tässä yllä olevassa kuvassa rivit l ja m ovat vaakasuuntaisia viivoja.
Vaakaviivan kaltevuus
Olemme jo maininneet, että vaakaviivan kaltevuus on nolla . Nyt opitaan kuinka vaakaviivan kaltevuus on nolla. Laskemme vaakasuoran viivan kaltevuuden käyttämällä kaavaa,
Kaltevuus = nousu/juoksu
TAI
Suoran kaltevuus = muutos y-koordinaatissa/muutos x-koordinaatissa
Missä nousu on korkeus, jonka viiva saavuttaa ajaessaan vasemmalta oikealle, koska tiedämme jo, että vaakaviiva on yhdensuuntainen x-akselin kanssa ja on aina vakiokorkeudella, joten sanomme, että näillä viivoilla on nolla nousu, joten näiden viivojen kaltevuus on,
Siten kaltevuus = 0/ajo = 0
Siten päätellään, että vaakaviivan kaltevuus on nolla.
Vaakaviivan piirtäminen
Vaakasuuntaiset viivat on helppo piirtää alla kuvattujen vaiheiden avulla,
Vaihe 1: Ota suorakulmaiselta tasolta piste, jolle meidän on löydettävä vaakaviiva. Oletetaan, että piste on (1, 2)
Vaihe 2: Merkitsee pisteen y-koordinaatin. Tässä tapauksessa y-koordinaatti on 2.
Vaihe 3: Merkitse muut pisteet, joissa y-koordinaatti on sama kuin vaiheen 1 piste. Olkoon muut pisteet (-2, 2), (0, 2) ja (7, 2)
Vaihe 4: Yhdistä kaikki pisteet saadaksesi jana ja pidennä niitä molemmilta puolilta saadaksesi vaakasuora viiva.
Tämä on vaadittu vaakaviiva, joka kulkee pisteen (1, 2) läpi ja jonka kaltevuus on nolla.

Vaakaviivayhtälö
Tiedämme, että 2D-koordinaattijärjestelmän suoran yhtälö on,
y = mx + c
Missä,
- m on viivan kaltevuus
- c on y-akselin leikkauspiste
Tiedämme, että vaakaviivalla kaltevuus on nolla. Korvaamalla tämän arvon yllä olevassa yhtälössä saamme vaakaviivan yhtälön olevan,
y = 0x + c
y = c
Missä c on vakio.
Siten yllä oleva yhtälö y = c on vaakaviivan yhtälö.
Tämä yhtälö tarkoittaa, että vaakaviiva on viiva, joka kulkee kaikkien niiden suorakulmaisen pisteen läpi, joissa y-koordinaatti on yhtä suuri kuin 'c'. Tällä viivaleikkauksella ei ole x-koordinaattia, joten tämä viiva ei koskaan leikkaa x-akselia ja se leikkaa y-akselin pisteessä (0, c).
Voidaan siis sanoa, että vaakaviivan yhtälö on, y = c(vakio) ja se kulkee pisteen (a, c) kautta, jossa a voi saada minkä tahansa arvon ja c on aina vakio.
Vaakaviivatesti
Testi, jota käytetään määrittämään, onko funktio yksi-yhteen-funktio vai ei, on vaakaviivatesti. Vaakaviivatestissä piirretään vaakasuora viiva, joka kulkee funktion minkä tahansa pisteen kautta ja jos viivat leikkaavat funktion jossain muussa pisteessä, funktio EI ole yksi-yhteen-funktio. Jotta funktio olisi yksi yhteen, sen on läpäistävä vaakaviivatesti, eli minkä tahansa vaakaviivan on leikattava funktio vain kerran.
Tiedämme, että yksi-yhteen-funktiot ovat funktioita, joissa jokaiselle x:n arvolle meillä on vain yksi y:n arvo. Joten, jos vaakaviiva kulkee funktion läpi ja leikkaa sen vain kerran, voimme sanoa, että y:n ainutlaatuiselle arvolle meillä on yksilöllinen arvo x. Mutta jos vaakaviiva leikkaa funktion useammin kuin kerran, saamme kaksi arvoa y:n ainutlaatuiselle arvolle, mikä ei pidä paikkaansa yksi-yhteen-funktion tapauksessa.
Vaakaviivatesti auttaa meitä määrittämään, onko funktio yksi-yksi-funktio. Tämä voidaan ymmärtää alla lisätyn kuvan avulla.

Ensimmäisessä kuvassa funktio on yksi yhteen, koska vaakaviiva kulkee vain yhden funktion pisteen läpi.
Toisessa kuvassa funktio EI ole yksi yhteen, koska vaakaviiva kulkee useamman kuin yhden funktion pisteen läpi.
Vaaka- ja pystysuorat viivat
Vaakaviivat ovat viivoja, jotka ovat yhdensuuntaisia maan tai horisontin kanssa. Näitä linjoja kutsutaan myös nukkumislinjoiksi. Karteesisessa järjestelmässä nämä viivat ovat yhdensuuntaisia x-akselin kanssa, kun taas pystysuorat viivat ovat kohtisuorassa vaakasuuntaisia viivoja vastaan, niitä kutsutaan seisoviksi viivoiksi. ja ovat yhdensuuntaisia y-akselin kanssa karteesisessa järjestelmässä.
Vaakaviivat ovat viivoja, jotka kulkevat vasemmalta oikealle suorakulmaisessa järjestelmässä, kun taas pystyviivat ovat viivoja, jotka kulkevat ylös ja alas karteesisessa järjestelmässä.
Pysty- ja vaakaviivat ovat kohtisuorassa toisiinsa nähden. Alla lisätyssä kuvassa on pystysuora ja vaakasuora viiva.

Erot pystysuorien ja vaakasuuntaisten viivojen välillä
Pystysuorien ja vaakaviivojen väliset erot on helppo ymmärtää tutkimalla alla olevaa taulukkoa.
| Vaakaviiva | Pystysuora viiva |
|---|---|
| Nämä viivat ovat yhdensuuntaisia maan tai horisontin kanssa. | Nämä rivit ovat kohtisuorassa maahan tai horisonttiin. |
| Vaakaviivan kaltevuus on nolla. | Pystyviivan kaltevuus on määrittelemätön. |
| Vaakaviiva teki nollan kulman horisontin kanssa. | Pystyviiva loi 90 asteen kulman horisontin kanssa. |
| Pisteen (h, k) läpi kulkevan vaakaviivan yhtälö on, y = k | Pisteen (h, k) läpi kulkevan pystysuoran suoran yhtälö on, x = h |
| Vaakaviivat ovat yhdensuuntaisia x-akselin kanssa karteesisessa järjestelmässä. | Pystysuorat viivat ovat yhdensuuntaisia y-akselin kanssa karteesisessa järjestelmässä. |
| Esimerkkejä vaakasuuntaisista viivoista ovat
| Esimerkkejä pystysuoraa viivaa edustavista viivoista ovat
|
Lyhyt huomautus vaakaviivasta
Matematiikan vaakaviiva on täysin tasainen, yhdensuuntainen horisontin kanssa. Se kulkee vasemmalta oikealle ja sen kaltevuus on 0. Geometriassa se esitetään suorana viivana, joka yhdistää mitkä tahansa kaksi samalla korkeudella olevaa pistettä tasossa. Vaakaviivan yhtälö on muotoa (y = k), jossa (k) on vakioarvo, joka edustaa viivan korkeutta y-akselilla.
Lue lisää:
css-kääreteksti
- Linjojen tyypit
- Yhdensuuntaiset viivat
- Kuinka lisätä vaakaviiva HTML:ään?
- Kuinka käyttää täydellistä vaakasuuntaista rivitilaa HTML:ssä?
- Vaaka- ja pystysuorien viivojen piirtäminen Android-sovelluksessa XML:n avulla
Esimerkkejä vaakasuuntaisista viivoista
Esimerkki 1: Etsi pisteen (1, -1) kautta kulkevan vaakaviivan yhtälö.
Ratkaisu:
Tiedämme, että vaakaviivan kaltevuus on m = 0.
Annettu piste (1, -1)
Pisteen kautta kulkevan suoran yhtälö (x1, ja1) ja jonka kaltevuus (m) on,
ja ja1= m(x – x1)
Korvaamalla arvot yllä olevassa yhtälössä saamme,
y – (-1) = 0 (x – 1)
ja +1 = 0
y = -1
Siten pisteen (1, -1) läpi kulkevan vaakaviivan yhtälö on, y = -1
Esimerkki 2: Etsi pisteen (5, 9) kautta kulkevan vaakaviivan yhtälö.
Ratkaisu:
numpy standardipoikkeama
Tiedämme, että vaakaviivan kaltevuus on m = 0.
Annettu piste (5, 9)
Pisteen kautta kulkevan suoran yhtälö (x1, ja1) ja jonka kaltevuus (m) on,
ja ja1= m(x – x1)
Korvaamalla arvot yllä olevassa yhtälössä saamme,
y – (9) = 0 (x – 5)
ja – 9 = 0
y = 9
Siten pisteen (5, 9) läpi kulkevan vaakaviivan yhtälö on, y = 9
Esimerkki 3: Etsi vaakaviivan yhtälö, kun suoran y-leikkauspiste on 5.
Ratkaisu:
Vaakaviivan yhtälö on,
y = k
missä k on y-leikkaus
Annettu
- k = 5
Vaakaviivan yhtälö,
y = 5
Siten yhtälön vaakaviiva, jossa y-leikkaus on 5, on y = 5
Esimerkki 4: Etsi vaakaviivan yhtälö, kun suoran y-leikkauspiste on -11/3.
Ratkaisu:
Vaakaviivan yhtälö on,
y = k
missä k on y-leikkaus
Annettu
- k = -11/3
Vaakaviivan yhtälö,
y = -11/3
3v = -11
3v + 11 = 0
Siten yhtälön vaakaviiva, jossa y-leikkaus on -11/3, on 3y + 11 = 0
Vaakaviivat – UKK
Mitä ovat vaakaviivat?
Vaakaviivat ovat viivoja, jotka ovat yhdensuuntaisia horisontin tai maan kanssa. Karteesisessa järjestelmässä vaakaviivat ovat yhdensuuntaisia x-akselin kanssa.
Mikä on vaakaviivan yhtälö?
Vaakaviivan yhtälö on,
y = k
missä k on y-akselin leikkauspiste.
Mikä on vaakaviivan kaltevuus?
Vaakaviivan kaltevuus on aina nolla, koska ne muodostavat nollan asteen kulman x-akselin kanssa.
Mitkä ovat esimerkkejä vaakasuuntaisista viivoista?
Esimerkkejä vaakasuuntaisista viivoista ovat
- Suora tie
- Portaiden alaosa
- Minkä tahansa hahmon pohja jne.
Mikä on maapallon vaakasuuntaisten viivojen nimi?
Maapallolla kulkevia vaakasuuntaisia viivoja kutsutaan leveysasteiksi ja ne kulkevat yhdensuuntaisesti päiväntasaajan kanssa.
Mitkä ovat vaakasuuntaisten viivojen ominaisuudet?
Vaakaviivojen erilaiset ominaisuudet ovat,
- Ne ovat yhdensuuntaisia maan, horisontin ja x-akselin kanssa.
- Ne ovat kohtisuorassa y-akseliin nähden.
- Vaakaviivan kaltevuus on nolla jne.
Mikä viiva on pysty- ja vaakasuora?
Pystyviiva on yhdensuuntainen y-akselin kanssa ja kulkee suoraan ylös ja alas koordinaattitasossa, kun taas vaakaviiva on yhdensuuntainen x-akselin kanssa ja kulkee suoraan vasemmalle ja oikealle.
Mikä on vaaka- ja pystysuoran viivan kaltevuus?
Viivan kaltevuus osoittaa sen jyrkkyyden ja suunnan. Se lasketaan pystysuuntaisen muutoksen ja vaakasuuntaisen muutoksen suhteena kahden pisteen välillä viivalla.
Mitkä ovat vaaka- ja pystysuorat pisteviivat?
Vaakaviivat ulottuvat vasemmalta oikealle tai oikealta vasemmalle ja kulkevat yhdensuuntaisesti x-akselin kanssa, kun taas pystysuorat viivat ulottuvat ylös ja alas ja kulkevat yhdensuuntaisesti y-akselin kanssa. Nämä kaksi linjatyyppiä ovat kohtisuorassa toisiinsa nähden.
