Yksikköympyrä on ympyrä, jonka säde on 1. Yksikköympyrän keskipiste on origossa (0,0) akselilla. The ympärysmitta Yksikköympyrän pinta-ala on 2π yksikköä, kun taas yksikköympyrän pinta-ala on π yksikköä2. Se sisältää kaikki Circlen ominaisuudet. Yksikköympyrällä on yhtälö x2+ ja2= 1. Tämä yksikköympyrä auttaa määrittämään erilaisia trigonometrisiä käsitteitä.
Yksikköympyrä
Yksikköympyrä on usein merkitty S:llä1yleistäminen korkeampiin ulottuvuuksiin on yksikköpallo. Ymmärretään tarkemmin Unit Circle-, Formula- ja Solved-esimerkeistä alla.
Mikä on Unit Circle?
Yksikköympyrä on ympyrä, jonka säde on yksi(1) yksikkö. Käytämme karteesista tasoa piirtämään yksikköympyrän ja yksikköympyrä on 2 asteen polynomi, jossa on kaksi muuttujaa. Yksikköympyrällä on useita sovelluksia trigonometriassa ja algebrassa, ja sitä käytetään pääasiassa erilaisten trigonometristen suhteiden, kuten sin x, cos x, tan x ja muiden, arvojen löytämiseen.
Yksikköympyrän määritelmä
Matematiikassa yksikköympyrä määritellään sellaisen kiinteän pisteen paikaksi, joka on yhden yksikön etäisyydellä ympyrän keskustasta. Yksikköympyrän säde on yksi yksikkö ja tästä syystä nimi yksikköympyrä.
Yksikköympyrän yhtälö
Tiedämme, että minkä tahansa ympyrän yhtälö, jonka keskipiste (h, k) ja säde 'r' on,
(x – h) 2 + (y – k) 2 = r 2
Yksikköympyrän osalta tiedämme, että r on 1 yksikkö, joten yksikköympyrän yhtälö on,
(x – h) 2 + (y – k) 2 = 1
Yksikköympyrän kaava
Jos yksikköympyrän keskipiste on origo, eli (h, k) = (0, 0), niin yksikköympyrän yhtälö on,
x 2 + ja 2 = 1
Yksikköympyrä on esitetty alla lisätyssä kuvassa, jonka keskikoordinaatit h, k ja kun ympyrä on origossa, arvot h ja k ovat nolla ja säde AP on yhtä suuri kuin 1 yksikkö.
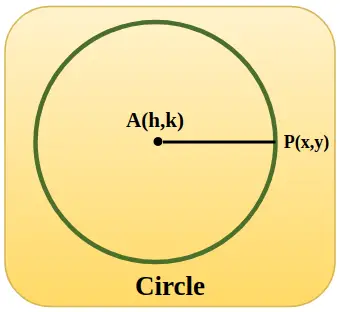
Trigonometriset funktiot yksikköympyrän avulla
Pythagoras-lauseen soveltamista yksikköympyrässä voidaan paremmin käyttää trigonometristen funktioiden ymmärtämiseen. Tarkastellaan tätä varten suorakulmaista kolmiota, joka on sijoitettu suorakulmaisen koordinaattitason yksikköympyrän sisään. Jos huomaamme, tämän ympyrän säde tarkoittaa suorakulmaisen kolmion hypotenuusaa.
Ympyrän säde muodostaa vektorin. Tämä johtaa kulman, sanotaan θ, muodostumiseen positiivisen x-akselin kanssa. Oletetaan, että x on oikean kolmion kantapituus ja y vastaavasti korkeuspituus. Myös sädevektorin päätepisteiden koordinaatit ovat vastaavasti (x, y).
Suorakulmaisessa kolmiossa on sivut 1, x ja y. Trigonometrinen suhde voidaan laskea nyt seuraavasti:
sin θ = Korkeus/Hypotenuusa = y/1
cos θ = emäs/hypotenuusa = x/1
Nyt,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Korvaamalla θ:n arvot saadaan kaikkien trigonometristen funktioiden pääarvot. Samalla tavalla löytyy trigonometristen funktioiden arvot eri arvoilla.
Yksikköympyrä Sin Cosin ja Tanin kanssa
Mikä tahansa yksikköympyrän piste, jonka koordinaatit (x, y), esitetään trigonometristen identiteettien avulla muodossa, (cosθ, sinθ). Säteen kulmien koordinaatit edustavat θ-arvojen kosinia ja siniä tietylle θ:n arvolle ja sädeviivalle. Meillä on cos θ = x ja sin θ = y. Ympyrässä on neljä osaa, joista kukin sijaitsee yhdessä kvadrantissa ja muodostaa kulman 90°, 180°, 270° ja 360°. Säteen arvot ovat -1:n ja 1:n välillä. Myös sin θ ja cos θ -arvot ovat vastaavasti välillä 1 ja -1.
Yksikköympyrä ja trigonometriset identiteetit
Kotangentin, sekantin ja kosekantin yksikköympyrän trigonometriset identiteetit voidaan laskea käyttämällä sin, cos ja tan identiteettiä. Lopulta saadaan suorakulmainen kolmio, jonka sivut ovat 1, x ja y. Yksikköympyrän identiteetit voidaan ilmaista seuraavasti:
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sek θ = 1/x
- cosec θ = 1/y
- pinnasänky θ = x/y
Yksikköympyräkaavio
Yksikköympyräkaavio on kaavio, joka sisältää trigonometrisen funktion sinin ja kosinin arvon eri kulmille. Saman yksikköympyräkaavio on lisätty alle,
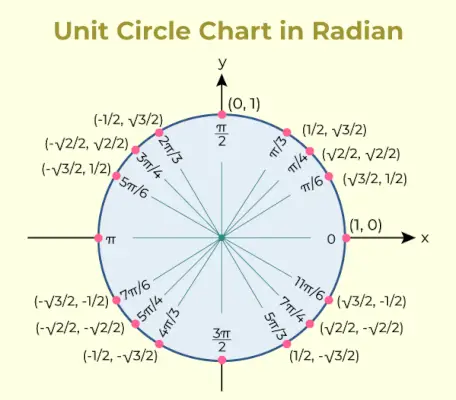
Yksikköympyrätaulukko
Yksikköympyrätaulukossa käytettyjä trigonometrisia suhteita käytetään listaamaan yksikköympyrän pisteiden koordinaatit, jotka vastaavat yhteisiä kulmia.
| Kulmat | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| ilman | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| niin | 0 | 1/√(3) | 1 | √(3) | Ei määritelty |
| csc | Ei määritelty | 2 | √(2) | 23) | 1 |
| sek | 1 | 23) | √(2) | 2 | Ei määritelty |
| pinnasänky | Ei määritelty | √(3) | 1 | 1/√(3) | 0 |
Yksikköympyrän Pythagoraan identiteetit
Pythagoralaista identiteettiä on kolme ja ne kaikki on helppo todistaa käyttämällä yksikköympyrän käsitettä, joita kolme Pythagoralaista identiteettiä ovat,
- ilman2θ + cos2θ = 1
- 1 + niin2θ = sek2i
- 1 + pinnasänky2θ = kosek2i
Yksikköympyrän monimutkainen taso
Monimutkaiset numerot ja Complex Plane on helppo selittää käyttämällä yksikköympyrän käsitettä. Yksikköympyrän yhtälö kompleksisessa muodossa on,
|z| = 1
TAI
x 2 + ja 2 = 1
Eulerin muodossa kompleksiluku esitetään muodossa,
z = e se = cos t + i(sin t)
Lue lisää
Ratkaistiin esimerkkejä yksikköympyrästä
Q1: Todista, että piste Q on yksikköympyrällä, Q = [1/√(6), √4/√6]
Ratkaisu:
Annettu,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Yksikköympyrän yhtälö on,
x2+ ja2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Siten piste Q[1/√(6), √4/√6] ei ole yksikköympyrällä.
Q2: Laske niin 30 O käyttämällä yksikköympyrän sin- ja cos-arvoja.
Ratkaisu:
tan 30° käyttämällä sin- ja cos-arvoja,
tan 30° = (sin 30°)/ (cos 30°)
- ilman 30° = 1/2
- cos 30° = √(3)/2
rusketus 30° = 1/2/√(3)/2
rusketus 30° = 1/√(3)
Q3: Tarkista, onko piste P [1/2, √(3)/2] yksikköympyrässä.
Ratkaisu:
Annettu,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Yksikköympyrän yhtälö on,
- x2+ ja2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Harjoittele kysymyksiä yksikköympyrässä
Q1. Tarkista, sijaitsevatko pisteet A (1/2, 3/2) yksikköympyrällä.
Q2. Tarkista, sijaitsevatko pisteet A (2, 1/2) yksikköympyrällä.
Q3. Etsi cos 240°:n arvo
Q4. Etsi tan 320°:n arvo
Q5. Etsi sin 160°:n arvo
Yksikköympyrä – UKK
Mikä on Unit Circle?
Yksikköympyrä määritellään pisteen sijainniksi yhden yksikön päässä kiinteästä pisteestä. Sen keskipiste on (0,0) ja sen säteen arvo on 1.
Kuinka tarkistaa, onko piste yksikköympyrässä?
Mikä tahansa 2D-tasossa oleva piste, joka on muotoa (x, y), sijoitetaan yksikköympyrän yhtälöön x2+ ja2= 1 varmistaaksesi, sijaitseeko se ympyrässä vai ei.
Mikä on yksikköympyrän kaava?
Yksikköympyrän kaava on kaava, jota käytetään edustamaan yksikköympyrää algebrallisesti. Yksikköympyrän kaava annetaan seuraavasti,
x 2 + ja 2 = 1
Miksi sitä kutsutaan Unit Circleksi?
Yksikköympyrää kutsutaan yksikköympyräksi, koska sen säde on yksi(1) yksikköä.
muuntaa str int:ksi
