Monikulmio matematiikassa on kaksiulotteinen muoto, joka koostuu suorista viivoista, jotka muodostavat suljetun monikulmioketjun. Sana polygon tulee sanoista poly ja gon, jotka tarkoittavat monia ja sivuja.
Monikulmiot voivat olla yksinkertaisia tai itsensä leikkaavia. Yksinkertainen monikulmio ei leikkaa itseään, paitsi peräkkäisten segmenttien yhteisissä päätepisteissä. Monikulmioketju, joka ylittää itsensä, muodostaa itsensä leikkaavan monikulmion. Monikulmiot voidaan myös luokitella koveriksi tai kuperiksi.
Tässä artikkelissa olemme maininneet yksityiskohtaisesti monikulmioista ja niiden tyypeistä, kaavoista ja esimerkeistä.
| Tärkeitä faktoja polygoneista | |
|---|---|
| Monikulmion sisäkulmien summa | (n–2) × 180° |
| Diagonaalien lukumäärä monikulmiossa | n(n–3)/2 |
| Säännöllisen monikulmion sisäkulma | {(n–2) × 180°}/n |
| Säännöllisen monikulmion ulkokulma | 360°/n |
Sisällysluettelo
- Mitä ovat polygonit?
- Monikulmiokaavio sivujen lukumäärän perusteella
- Polygonien ominaisuudet
- Monikulmion muodot
- Polygonien tyypit
- Monikulmiokaavat
- Kulmat monikulmioissa
- UKK
Mitä ovat polygonit?
Termi 'monikulmio' tulee kreikan sanasta polugonos, jossa 'poly' tarkoittaa 'monia' ja 'gon' tarkoittaa 'kulmaa'. Yleensä monikulmio on suorista viivoista muodostettu suljettu hahmo, jonka sisäkulmat muodostavat nämä rivit. Suljetun muodon muodostamiseksi tarvitaan vähintään kolmen rivin segmenttejä. Se tunnetaan yleisesti kolmiona tai 3-kulmaisena. Yleinen termi n-sivuiselle monikulmiolle on n-kulmio.
Monikulmion määritelmä
Monikulmiot ovat litteitä, kaksiulotteisia hahmoja, jotka koostuvat suorista sivuista, jotka muodostavat täysin suljetun muodon. Geometriassa monikulmio on tasokuva, joka koostuu viivasegmenteistä, jotka on yhdistetty muodostamaan suljetun monikulmioketjun. Ne koostuvat suorista sivuista, eivät kaarevista, ja niissä voi olla mikä tahansa määrä sivuja. Jotkut erityyppiset polygonit ovat: avoimia, vain rajallisia, suljettuja ja itsensä leikkaavia.
Geometriassa monikulmio määritellään suljetuksi, kaksiulotteiseksi muodoksi, joka on tasainen tasossa ja jota ympäröivät suorat sivut.
Monikulmiosta puuttuu kaarevia sivuja, ja sen reunat ovat suoria segmenttejä, jotka määrittävät sen rajan. Näiden reunojen kohtaamispisteitä kutsutaan kärkipisteiksi tai kulmiksi.
Esimerkkejä monikulmioista
Matemaattisesti kolmiot, kuusikulmiot, viisikulmiot ja nelikulmiot ovat esimerkkejä monikulmioista. Tosielämän esimerkkejä Polygonista ovat kannettavan tietokoneen, television, matkapuhelimen suorakaiteen muotoinen näyttö; suorakaiteen muotoinen jalkapallokenttä tai leikkipaikka, Bermudan kolmio ja Egyptin kolmion muotoiset pyramidit.

Monikulmion osat
Monikulmio koostuu kolmesta peruskomponentista:
- Polygonin sivut: Monikulmion sivut ovat suljetun alueen määrittävien polygonien rajat.
- Vertices: Piste, jossa kaksi sivua kohtaavat, tunnetaan kärjenä.
- Kulmat: Polygonissa on sekä sisä- että ulkokulmia. Sisäkulma muodostuu monikulmion suljetun alueen sisällä sen sivujen leikkauspisteestä.
Monikulmiokaavio sivujen lukumäärän perusteella
Monikulmion nimikkeistö määritellään niiden sivujen lukumäärän perusteella. Se on merkitty n-kulmioksi, missä 'n' tarkoittaa sivujen lukumäärää. Monikulmiot tunnistetaan yleensä niiden reunojen määrän perusteella. Esimerkiksi monikulmiota, jossa on viisi sivua, kutsutaan 5-kulmaiseksi, kun taas yhtä, jossa on kymmenen sivua, kutsutaan 10-kulmaiseksi.
| Monikulmiokaavio | ||||
|---|---|---|---|---|
| Monikulmion muodon nimet | Sivujen lukumäärä | Huippupisteiden lukumäärä | Diagonaalien lukumäärä | Sisäkulmamitta säännölliseen muotoon |
| Kolmio | Monikulmiot, joissa 3 sivua | 3 java-merkkijonon muunnos int:ksi | 0 | 60° |
| Nelikulmainen | Monikulmiot, joissa 4 sivua | 4 | 2 | 90° |
| Pentagon | Monikulmiot, joissa 5 sivua | 5 | 5 | 108° |
| Kuusikulmio | Monikulmiot, joissa 6 sivua | 6 | 9 | 120° |
| Seitsenkulmio | Monikulmiot, joissa on 7 sivua | 7 | 14 | 128,571° |
| Kahdeksankulmio | Monikulmiot, joissa 8 sivua | 8 | kaksikymmentä | 135° |
| Nonagon | Monikulmiot, joissa 9 sivua | 9 | 27 | 140° |
| Decagon | Monikulmiot, joissa on 10 sivua | 10 | 35 | 144° |
| Hendecagon | Monikulmiot, joissa on 11 sivua | yksitoista | 44 | 147,273° |
| Dodecagon | Monikulmiot, joissa 12 sivua | 12 | 54 | 150° |
Polygonien ominaisuudet
Polygonien ominaisuudet tunnistavat ne helposti. Seuraavat ominaisuudet auttavat monikulmioiden tuntemisessa helposti:
- Monikulmio on suljettu muoto, jossa ei ole avoimia päitä. Alku- ja loppupisteen tulee olla samat.
- Se saa tasomaisen muodon, joka koostuu viivasegmenteistä tai suorista viivoista, jotka yhdessä muokkaavat kuviota.
- Kaksiulotteisena kokonaisuutena monikulmio on olemassa vain pituuden ja leveyden mitoissa, ilman syvyyttä tai korkeutta.
- Siinä on kolme tai useampia sivuja monikulmion muodostamiseksi.
- Kulmat polygonissa voivat vaihdella. Se näyttää erillisen kokoonpanon.
- Monikulmion sivujen pituus voi vaihdella; se voi olla tai ei ole yhtä suuri monikulmion yli.
Monikulmion muodot
Monikulmio on litteä, kaksiulotteinen muoto, jolle on tunnusomaista suorat sivut, jotka on yhdistetty muodostamaan suljetun hahmon. Esimerkkejä monikulmion muodoista ovat:
- Kolmio
- Nelikulmainen
- Pentagon
- Kuusikulmio
- Seitsenkulmio
- Kahdeksankulmio
- Nonagon
- Decagon
Kolmio
- Siinä on 3 sivua ja 3 kärkeä.
- Siinä ei ole diagonaaleja.
- Sisäpuolen summa on 180°.
Nelikulmainen
- Siinä on 4 sivua ja 4 kärkeä.
- Siinä on 2 diagonaalia.
- Sisäkulman summa on 360°.
Pentagon
- Siinä on 5 sivua ja 5 kärkeä.
- Siinä on 5 diagonaalia.
- Sisäkulman summa on 540°.
Kuusikulmio
- Siinä on 6 sivua ja 6 kärkeä.
- Siinä on 9 diagonaalia.
- Sisäkulman summa on 720°.
Seitsenkulmio
- Siinä on 7 sivua ja 7 kärkeä.
- Siinä on 14 diagonaalia.
- Sisäkulman summa on 900°.
Kahdeksankulmio
- Siinä on 8 sivua ja 8 kärkeä.
- Siinä on 20 diagonaalia.
- Sisäkulman summa on 1080°.
Nonagon
- Siinä on 9 sivua ja 9 kärkeä.
- Siinä on 27 diagonaalia.
- Sisäkulman summa on 1260°.
Decagon
- Siinä on 10 sivua ja 10 kärkeä.
- Siinä on 35 diagonaalia.
- Sisäkulman summa on 1440°.
Polygonien tyypit
Sivuista ja kulmista riippuen polygonit voidaan luokitella eri tyyppeihin eri perusteella, kuten:
- Sivujen perusteella
- Kulmien perusteella
- Rajan perusteella
Monikulmiot sivujen perusteella
Monikulmiot voidaan luokitella niiden sivujen ominaisuuksien perusteella kahteen päätyyppiin:
- Säännöllinen monikulmio
- Epäsäännöllinen monikulmio
Säännöllinen monikulmio
Säännöllinen monikulmio erottuu siitä, että sen kaikki sivut ovat yhtä pitkiä ja kaikki sisäkulmat ovat yhtä suuret. Se voi olla sekä tasasivuinen että tasakulmainen. Esimerkkejä säännöllisistä monikulmioista ovat kolmio, nelikulmio, viisikulmio ja kuusikulmio.

Säännöllinen monikulmio
Epäsäännöllinen monikulmio
Epäsäännöllisellä monikulmiolla on eripituiset sivut ja eri mittaiset kulmat. Mikä tahansa monikulmio, joka ei täytä säännöllisen monikulmion kriteerejä, luokitellaan epäsäännöllisiksi. Yleisiä esimerkkejä epäsäännöllisistä monikulmioista ovat mittakaavakolmio, nelikulmiot, kuten suorakulmio, puolisuunnikas tai leija, sekä epäsäännölliset viisikulmio- ja kuusikulmiorakenteet.
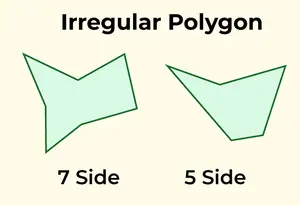
Epäsäännöllinen monikulmio
Polygonit kulmien perusteella
Monikulmiot voidaan luokitella niiden kulmien luonteen perusteella kahteen pääluokkaan:
- Kupera monikulmio
- Kovera monikulmio
Kupera monikulmio
Kuperalla monikulmiolla ei ole sisäkulmaa, joka on yli 180°. Kuperilla monikulmioilla voi olla kolme tai useampia sivuja. Kuperissa monikulmioissa kaikki diagonaalit ovat suljetun hahmon sisällä. Yleisiä esimerkkejä kuperista monikulmioista ovat kolmiot, kaikki kuperat nelikulmiot sekä säännölliset viisikulmiot ja kuusikulmiot
Kovera monikulmio
Koveralla monikulmiolla on vähintään yksi sisäkulma, joka on heijastuskulma ja osoittaa sisäänpäin. Koveralla polygonilla on vähintään neljä sivua. Tämän tyyppisessä monikulmiossa on vähintään yksi sisäkulma, joka on yli 180°. Koverissa polygoneissa jotkin lävistäjät ulottuvat suljetun kuvan ulkopuolelle. Esimerkkejä koverista monikulmioista ovat tikka tai nuolenpää nelikulmioissa sekä tietyt epäsäännölliset viisikulmiot ja kuusikulmiot.
Ero koveran vs kuperan monikulmion välillä
Katsotaanpa eroa kuperan ja koveran monikulmion välillä alla olevassa taulukossa:

| Kupera monikulmio | Kovera monikulmio |
|---|---|
| Kuperan muodon koko ympärysmitta ulottuu ulospäin ilman sisäänpäin painaumia. | Koverassa muodossa on vähintään yksi sisäänpäin osoittava osa, joka osoittaa kolhun olemassaolon. |
| Kuperassa monikulmiossa kaikki sisäiset kulmat ovat alle 180°. | Koverassa monikulmiossa on ainakin yksi sisäkulma, joka ylittää 180°. |
| Mikä tahansa viiva, joka yhdistää kaksi kuperan muodon kärkeä, on kokonaan muodon rajojen sisällä. | Mitä tahansa kahta koveran muodon kärkeä yhdistävä viiva voi tai ei leikkaa muodon sisäosia. |
Polygonit rajojen perusteella
Monikulmiot voidaan luokitella niiden rajojen luonteen perusteella kahteen päätyyppiin:
- Yksinkertainen monikulmio
- Monimutkainen monikulmio
Yksinkertainen monikulmio
Yksinkertaiselle monikulmiolle on ominaista yksittäinen, ei-leikkaava raja. Toisin sanoen se ei ylitä itseään, ja se koostuu yhdestä rajasta.
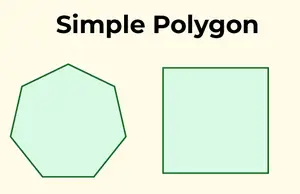
Yksinkertaiset polygonit
Monimutkainen monikulmio
Toisaalta monimutkainen monikulmio määritellään itse leikkaamalla. Se koostuu useammasta kuin yhdestä rajasta sen rakenteessa. Monimutkaisissa polygoneissa rajat leikkaavat, jolloin monikulmioon muodostuu useita erillisiä alueita.

Monimutkainen monikulmio
Lue lisää aiheesta Polygonien tyypit.
Monikulmiokaavat
Geometriassa on useita monikulmioihin liittyviä kaavoja. Jotkut yleisimmin käytetyistä ovat:
- Alueen kaava
- Kehäkaava
- Diagonaalien määrä
Kaikkia eri polygoneihin liittyviä kaavoja käsitellään alla:
Monikulmioiden alue
Monikulmion alue edustaa sen viemää kokonaistilaa kaksiulotteisessa tasossa, se määritetään erityisillä kaavoilla, jotka perustuvat sivujen lukumäärään ja monikulmion luokitukseen. Aluekaavat ovat seuraavat:
| Polygonin alue | Kaava |
|---|---|
| Kolmion alue | 1/2 × pohja × korkeus |
| Parallelogrammin alue | Pohja × korkeus |
| Suorakulmion alue | Pituus × Leveys |
| Squaren alue | (sivulla)2 |
| 1/2 × diagonaali1× diagonaali2 | |
| Trapeziumin alue | 1/2 × korkeus × rinnakkaisten sivujen summa |
| (5/2) × sivun pituus × Apothem | |
| Kuusikulmion alue | {(3√3)/2}puoli2 |
| Heptagonin alue | 3,643 × Sivu2 |
Monikulmion ympärysmitta
Kaksiulotteisen muodon kehä edustaa sen ulkoreunan kokonaispituutta. Monikulmioiden kehä lasketaan seuraavasti:
| Monikulmion ympärysmitta | Kaava |
|---|---|
| Kolmion kehä | Kolmen puolen summa |
| Parallelogrammin ympärysmitta | 2 (vierekkäisten sivujen summa) |
| Suorakulmion ympärysmitta | 2 (pituus + leveys) |
| Neliön ympärysmitta | 4 × sivu |
| Rombuksen ympärysmitta | 4 × sivu |
| Trapetsion ympärysmitta | Yhdensuuntaisten sivujen summa + ei-rinnakkaissivujen summa |
| Pentagonin kehä | 5 × sivu |
| Kuusikulman ympärysmitta | 6 × sivu |
| Heptagon ympärysmitta | 7 × sivu |
Monikulmion kaavan diagonaali
Monikulmion diagonaali on jana, joka muodostuu yhdistämällä kaksi pistettä, jotka eivät ole vierekkäisiä.
Diagonaalien lukumäärä monikulmiossa = n(n-3)/2,
Missä 'n' edustaa monikulmion sivujen määrää.
Lue lisää aiheesta Monikulmion kaavan diagonaali .
Kulmat monikulmioissa
Geometriassa monikulmion kulmat tarkoittavat monikulmion sivujen muodostamia kulmia sekä monikulmion sisällä että ulkona. Näin ollen monikulmiossa voi olla molemmat kulmat, ts.
- Sisäkulmat
- Ulkoiset kulmat
Keskustellaan näiden kulmien kaavasta yksityiskohtaisesti seuraavasti:
Monikulmioiden sisäkulmakaava
Monikulmion sisäkulmat ovat ne, jotka muodostuvat sen vierekkäisten sivujen väliin ja ovat yhtä suuret säännöllisen monikulmion tapauksessa. Sisäkulmien määrä vastaa monikulmion sivujen lukumäärää.
Sisäkulmien summa 'S' monikulmiossa, jossa on 'n'-sivut, lasketaan seuraavasti
S = (n - 2) × 180°
Missä 'n' tarkoittaa sivujen lukumäärää.
Polygonien ulkokulmakaava
Säännöllisen monikulmion jokainen ulkokulma muodostetaan laajentamalla sen yhtä sivua (joko myötäpäivään tai vastapäivään) ja mittaamalla tämän jatkeen ja viereisen sivun välinen kulma. Tavallisessa monikulmiossa kaikki ulkokulmat ovat yhtä suuret
Minkä tahansa monikulmion ulkokulmien kokonaissumma on kiinteä 360°
Siksi,
Kukin ulkokulma on 360°/n
Missä 'n' on sivujen lukumäärä.
Sisäisten ja vastaavien ulkokulmien summa monikulmion missä tahansa kärjessä on aina 180 astetta, mikä ilmaisee lisäsuhteen:
Sisäkulma + ulkokulma = 180°
Ulkokulma = 180° – Sisäkulma
Johtopäätös
- Monikulmio on suljettu kuvio, jota rajoittaa vähintään kolme janaa
- Sisäkulmien summa: N-sivuisen monikulmion kaikkien sisäkulmien summa saadaan kaavalla (n–2) × 180°.
- Diagonaalien määrä: Monikulmiolle, jossa on n sivua, diagonaalien lukumäärä lasketaan kaavalla n(n–3)/2.
- Diagonaalien muodostamat kolmiot: Monikulmion yhdestä kulmasta lävistyksiä yhdistämällä muodostuvien kolmioiden määrä on n–2.
- Säännöllisen monikulmion sisäkulma: Jokaisen sisäkulman mitta n-sivuisessa säännöllisessä monikulmiossa on {(n–2) × 180°}/n.
- Säännöllisen monikulmion ulkokulma: Jokaisen ulkokulman mitta n-sivuisessa säännöllisessä monikulmiossa on 360°/n.
Myös Lue
- Neliö
- Suunnikas
- Suorakulmio
Ratkaistiin esimerkkejä monikulmiosta matematiikassa
Esimerkki 1: Tarkastellaan nelikulmiota, jossa on neljä sivua. Laske kaikkien sen nelikulmion sisäkulmien summa.
Ratkaisu:
Kaava sisäkulmien summalle n-sivuisessa säännöllisessä monikulmiossa = (n − 2) × 180°
Nelikulman kaikkien sisäkulmien summa = (4 – 2) × 180°
Nelikulman kaikkien sisäkulmien summa = 2 × 180°
Nelikulman kaikkien sisäkulmien summa = 360°
Siksi nelikulmion kaikkien sisäkulmien summa on 360°.
Esimerkki 2: Tarkastellaan säännöllistä monikulmiota, jonka ulko- ja sisäkulmasuhde on 7:3. Määritä monikulmion tyyppi.
Ratkaisu:
Ulko- ja sisäkulman suhde on 7:3.
Oletetaan, että monikulmion ulko- ja sisäkulma ovat 7x ja 3x.
Minkä tahansa monikulmion ulko- ja sisäkulmien summa on 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Ulkokulma = 18°
Sivujen lukumäärä = 360°/ulkokulma
= 360°/18°
merkkijonojen lisääminen java= 20
Siksi annettu monikulmio on ikosagoni, koska siinä on 20 sivua.
Esimerkki 3: Polygonin jokainen ulkokulma on 90 astetta, määritä monikulmion tyyppi?
Ratkaisu:
Kaavan mukaan jokainen ulkokulma = 360°/n
Tässä n = sivujen lukumäärä.
90° = 360°/n
n = 360°/90° = 4
Näin ollen kyseessä oleva monikulmio on nelikulmio, koska sillä on neljä sivua.
Esimerkki 4: Sivut ovat 10 m, 10 m, 8 m, 8 m, 5 m, 5 m, 9 m, 9 m. Kuinka monta metriä köyttä tarvitaan kehälle?
Ratkaisu:
Kehälle tarvittavan köyden pituuden löytämiseksi meidän on laskettava kaikkien sivujen pituudet:
Kehä = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Kehä = 64 m.
Perimetriin tarvitaan siis yhteensä 64 metriä köyttä.
Harjoittele kysymyksiä polygoneista geometriassa
Seuraavassa on joitain harjoituskysymyksiä, jotka perustuvat monikulmioiden kaavaan:
Q1. Kun yksi viisikulmion kulma on 140°, määritä suurimman kulman koko, jos muut kulmat ovat suhteessa 1:2:3:4.
Q2. Jos monikulmion sisäkulmien summa on 160°, selvitä monikulmion sivujen lukumäärä.
Q3. Kahden säännöllisen monikulmion sivujen lukumäärä on suhteessa 2:3 ja niiden sisäkulmien suhde on 4:5. Etsi näiden polygonien sivujen lukumäärä.
Q4. Määritä kulmien kokonaissumma kuusikulmiossa.
Q5. Laske viisikulmion ulkokulmien summa.
Q6. Kuinka monta sivua kuusikulmiolla on?
- 4
- 6
- 8
- 10
Q7. Mikä seuraavista ei ole säännöllinen monikulmio?
- Kolmio
- Neliö
- Pentagon
- Suunnikas
Usein kysytyt kysymykset matematiikan polygoneista
Mikä on monikulmio matematiikassa?
Matematiikassa monikulmio viittaa suljettuun kaksiulotteiseen kuvioon, joka muodostuu kolmen tai useamman suoran yhdistämisestä. Termi monikulmio on johdettu kreikan kielestä, jossa poly- merkitsee monta ja gon edustaa kulmaa.
Mikä on pienin monikulmio?
Pienin muodostettu monikulmio on kolmio, jossa on kolme sivua.
Mikä on 20-gon?
20 kulmio on geometriselta 20-sivuinen monikulmio.
Mikä on monikulmion ulkoisten kulmien kokonaissumma?
Monikulmion ulkokulmien summa on 360°.
Voidaanko ympyrä luokitella monikulmioksi?
Monikulmio on suljettu muoto, joka koostuu suorista segmenteistä. Ympyrä on suljettu hahmo, mutta se on tehty käyrästä. Ympyrä ei siis ole monikulmio.
Mikä on monikulmion sisäkulmien summa?
Monikulmion sisäkulman summa saadaan kaavalla (n–2)×180°, missä n on monikulmion sivujen lukumäärä.
